4.3: Monotonic Functions and the First Derivative Test
( \newcommand{\kernel}{\mathrm{null}\,}\)
The method of the previous section for deciding whether there is a local maximum or minimum at a critical value is not always convenient. We can instead use information about the derivative f′(x) to decide; since we have already had to compute the derivative to find the critical values, there is often relatively little extra work involved in this method.
How can the derivative tell us whether there is a maximum, minimum, or neither at a point? Suppose that f′(a)=0. If there is a local maximum when x=a, the function must be lower near x=a than it is right at x=a. If the derivative exists near x=a, this means f′(x)>0 when x is near a and x<a, because the function must "slope up'' just to the left of a. Similarly, f′(x)<0 when x is near a and x>a, because f slopes down from the local maximum as we move to the right.
Using the same reasoning, if there is a local minimum at x=a, the derivative of f must be negative just to the left of a and positive just to the right. If the derivative exists near a but does not change from positive to negative or negative to positive, that is, it is positive on both sides or negative on both sides, then there is neither a maximum nor minimum when x=a. See the first graph in figure 5.1.1 and the graph in figure 5.1.2 for examples.
The derivative is f′(x)=cosx−sinx and from example 5.1.3 the critical values we need to consider are π/4 and 5π/4.
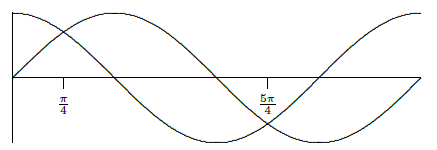
The graphs of sinx and cosx are shown in Figure 4.3.1. Just to the left of π/4 the cosine is larger than the sine, so \)f'(x)\) is positive; just to the right the cosine is smaller than the sine, so f′(x) is negative. This means there is a local maximum at \)\pi/4\). Just to the left of 5π/4 the cosine is smaller than the sine, and to the right the cosine is larger than the sine. This means that the derivative f′(x) is negative to the left and positive to the right, so f has a local minimum at 5π/4.

