15.2: Double Integrals over General Regions
( \newcommand{\kernel}{\mathrm{null}\,}\)
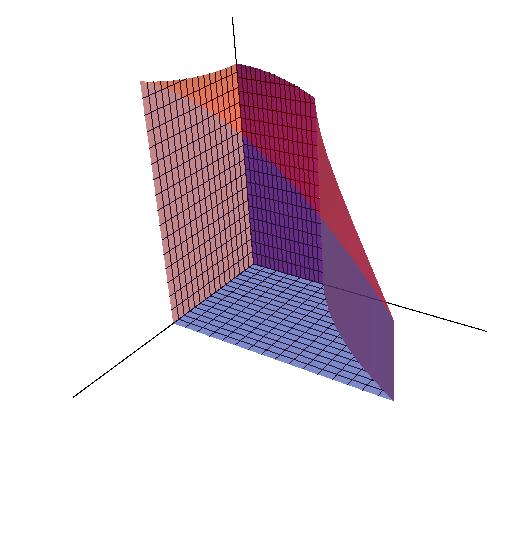
In Section 15.1, we notice that all bases of the objects are rectangular. In 15.2, the area under these objects are nonrectangular. However, the method of accumulation still works.
Introduction
In the Figure
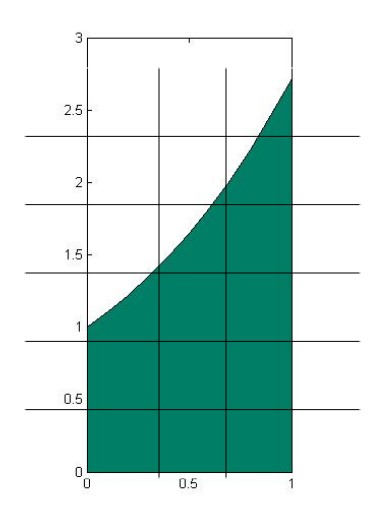
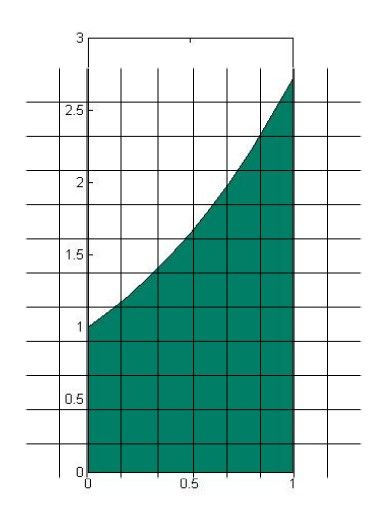
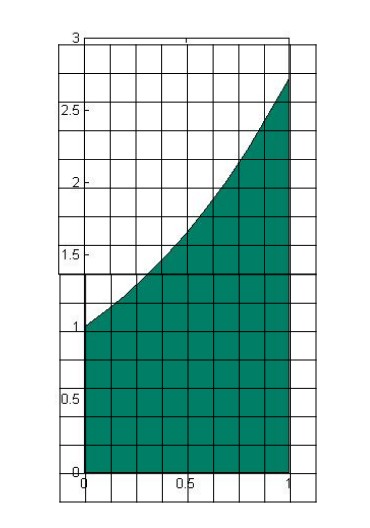
Let
- If R is defined by
- If R is defined by
Fubini's Theorem is usually used to calculate the volume of the objects that have nonrectangule bases.
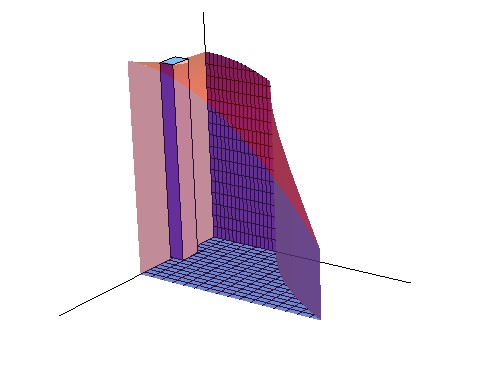
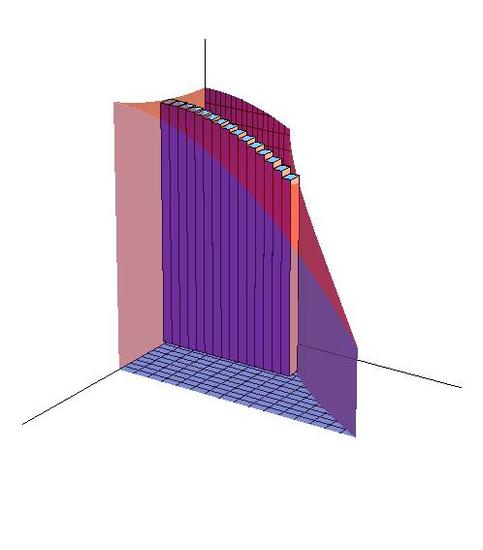
Just like the sample in 15.1,
Now, lets calculate the volume under the surface

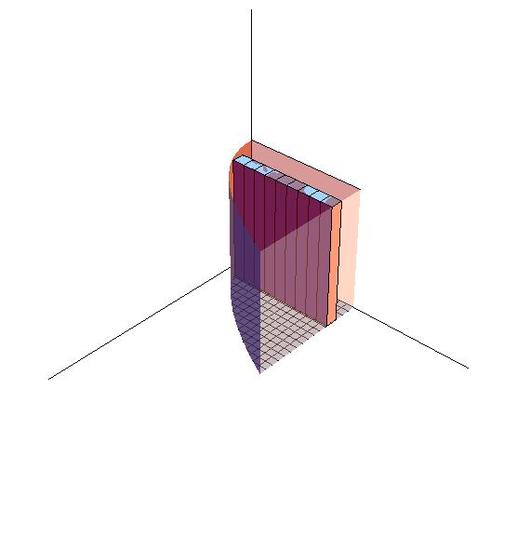
Reverse the order of integration of the function
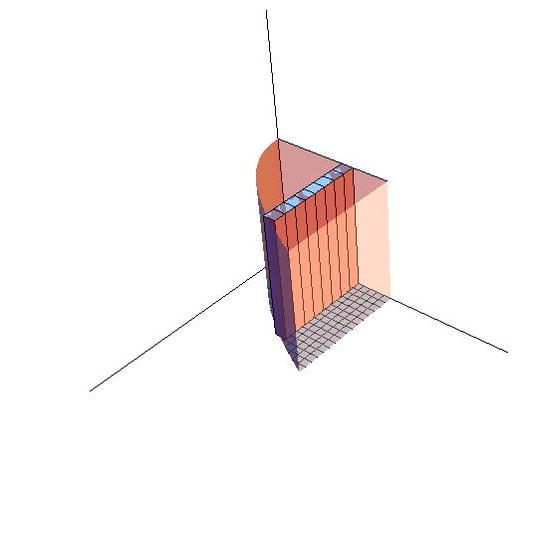
Reminder:
- As the equation is transformed, the domains of x and y are also transformed.
- When
- The order of
Calculate the volume above
In this case, the question become too complicated to be solved. Thus, we need to transform this equation.
Integrated by Justin Marshall.

