3.3.1: Examples
- Page ID
- 2173
Example 3.3.1.1: Beltrami Equations
\begin{eqnarray}
\label{belt1}\tag{3.3.1.1}
Wu_x-bv_x-cv_y&=&0\\
\label{belt2}\tag{3.3.1.2}
Wu_y+av_x+bv_y&=&0,
\end{eqnarray}
where \(W,\ a,\ b,\ c\) are given functions depending of \((x,y)\), \(W\not=0\) and the matrix
$$
\left(\begin{array}{cc}
a&b\\
b&c
\end{array}\right)
\]
is positive definite.
The Beltrami system is a generalization of Cauchy-Riemann equations. The function \(f(z)=u(x,y)+iv(x,y)\), where \(z=x+iy\), is called a quasiconform mapping, see for example [9], Chapter 12, for an application to partial differential equations.
Set
$$
A^1=\left(\begin{array}{cc}
W&-b\\
0&a
\end{array}\right),\ \
A^2=\left(\begin{array}{cc}
0&-c\\
W&b
\end{array}\right).
\]
Then the system (\ref{belt1}), (\ref{belt2}) can be written as
$$
A^1\left(\begin{array}{c}
u_x\\v_x
\end{array}\right)+
A^2\left(\begin{array}{c}
u_y\\v_y
\end{array}\right)=\left(\begin{array}{c}0\\0\end{array}\right).
\]
Thus,
\begin{eqnarray*}
C(x,y,\zeta)=\left|\begin{array}{cc}
W\zeta_1&-b\zeta_1-c\zeta_2\\
W\zeta_2&a\zeta_1+b\zeta_2
\end{array}\right|
=W(a\zeta_1^2+2b\zeta_1\zeta_2+c\zeta_2^2),
\end{eqnarray*}
which is different from zero if \(\zeta\not=0\) according to the above assumptions. Thus the Beltrami system is elliptic.
Example 3.3.1.2: Maxwell Equations
The Maxwell equations in the isotropic case are
\begin{eqnarray}
\label{max1}\tag{3.3.1.3}
c\ \text{rot}_x\ H&=&\lambda E+\epsilon E_t\\
\label{max2}\tag{3.3.1.4}
c\ \text{rot}_x\ E&=&-\mu H_t,
\end{eqnarray}
where
- \(E=(e_1,e_2,e_3)^T\) electric field strength, \(e_i=e_i(x,t)\), \(x=(x_1,x_2,x_3)\),
- \(H=(h_1,h_2,h_3)^T\) magnetic field strength, \(h_i=h_i(x,t)\),
- \(c\) speed of light,
- \(\lambda\) specific conductivity,
- \(\epsilon\) dielectricity constant,
- \(\mu\) magnetic permeability.
Here \(c,\ \lambda,\ \epsilon\) and \(\mu\) are positive constants.
Set \(p_0=\chi_t,\ p_i=\chi_{x_i}\), \(i=1,\ldots 3\), then the characteristic differential equation is
$$
\left|\begin{array}{cccccc}
\epsilon p_0/c&0&0&0&p_3&-p_2\\
0&\epsilon p_0/c&0&-p_3&0&p_1\\
0&0&\epsilon p_0/c&p_2&-p_1&0\\
0&-p_3&p_2&\mu p_0/c&0&0\\
p_3&0&-p_1&0&\mu p_0/c&0\\
-p_2&p_1&0&0&0&\mu p_0/c
\end{array}\right|=0.
\]
The following manipulations simplifies this equation:
- multiply the first three columns with \(\mu p_0/c\),
- multiply the 5th column with \(-p_3\) and the the 6th column with \(p_2\) and add the sum to the 1st column,
- multiply the 4th column with \(p_3\) and the 6th column with \(-p_1\) and add the sum to the 2th column,
- multiply the 4th column with \(-p_2\) and the 5th column with \(p_1\) and add the sum to the 3th column,
- expand the resulting determinant with respect to the elements of the 6th, 5th and 4th row.
We obtain
$$
\left|\begin{array}{ccc}
q+p_1^2&p_1p_2&p_1p_3\\
p_1p_2&q+p_2^2&p_2p_3\\
p_1p_3&p_2p_3&q+p_3^2
\end{array}\right|=0,
\]
where
$$
q:=\frac{\epsilon\mu}{c^2}p_0^2-g^2
\]
with \(g^2:=p_1^2+p_2^2+p_3^2\). The evaluation of the above equation leads to \(q^2(q+g^2)=0\), i. e.,
$$
\chi_t^2\left(\frac{\epsilon\mu}{c^2}\chi_t^2-|\nabla_x\chi|^2\right)=0.
\]
It follows immediately that Maxwell equations are a hyperbolic system, see an exercise.
There are two solutions of this characteristic equation. The first one are characteristic surfaces \(\mathcal{S}(t)\), defined by \(\chi(x,t)=0\), which satisfy \(\chi_t=0\). These surfaces are called stationary waves The second type of characteristic surfaces are defined by solutions of
$$
\frac{\epsilon\mu}{c^2}\chi_t^2=|\nabla_x\chi|^2.
\]
Functions defined by \(\chi=f(n\cdot x-Vt)\) are solutions of this equation.
Here is \(f(s)\) an arbitrary function with \(f'(s)\not=0\), \(n\) is a unit vector and \(V=c/\sqrt{\epsilon\mu}\).
The associated characteristic surfaces \(\mathcal{S}(t)\) are defined by
$$
\chi(x,t)\equiv f(n\cdot x-Vt)=0,
\]
here we assume that \(0\) is in he range of \(f:\ \mathbb{R}^1\mapsto\mathbb{R}^1\). Thus, \(\mathcal{S}(t)\) is defined by \(n\cdot x-Vt=c\), where \(c\) is a fixed constant. It follows that the planes \(\mathcal{S}(t)\) with normal \(n\) move with speed \(V\) in direction of \(n\), see Figure 3.3.1.1.
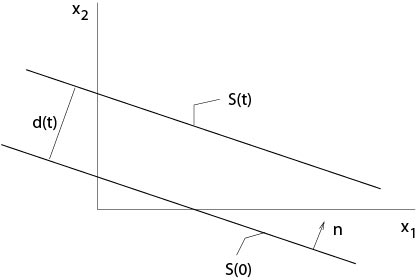
Figure 3.3.1.1: \(d'(t)\) is the speed of plane waves
\(V\) is called speed of the plane wave \(\mathcal{S}(t)\).
Remark. According to the previous discussions, singularities of a solution of Maxwell equations are located at most on characteristic surfaces.
A special case of Maxwell equations are the telegraph equations, which follow from Maxwell equations if \(\text{\div}\ E=0\) and \(\text{div}\ H=0$\) i. e., \(E\) and \(H\) are fields free of sources. In fact, it is sufficient to assume that this assumption is satisfied at a fixed time \(t_0\) only, see an exercise.
Since
$$
\text{rot}_x\ \text{rot}_x\ A=\mbox{grad}_x\ \text{div}_x\ A-\triangle_xA
\]
for each \(C^2\)-vector field \(A\), it follows from Maxwell equations the uncoupled system
\begin{eqnarray*} \triangle_xE&=&\frac{\epsilon\mu}{c^2}E_{tt}+\frac{\lambda\mu}{c^2}E_t\\
\triangle_xH&=&\frac{\epsilon\mu}{c^2}H_{tt}+\frac{\lambda\mu}{c^2}H_t.
\end{eqnarray*}
Example 3.3.1.3: Equations of Gas Dynamics
Consider the following quasilinear equations of first order.
$$
v_t+(v\cdot\nabla_x)\ v+\frac{1}{\rho} \nabla_x p =f\ \ \ \mbox{(Euler equations)}.
\]
Here is
- \(v=(v_1,v_2,v_3)\) the vector of speed, \(v_i=v_i(x,t)\), \(x=(x_1,x_2,x_3)\),
- \(p\) pressure, \(p=(x,t)\),
- \(\rho\) density, \(\rho=\rho(x,t)\),
- \(f=(f_1,f_2,f_3)\) density of the external force, \(f_i=f_i(x,t)\),
\((v\cdot\nabla_x)v\equiv (v\cdot\nabla_x v_1,v\cdot\nabla_x v_2,v\cdot\nabla_x v_3))^T\).
The second equation is
$$
\rho_t+v\cdot\nabla_x\rho+\rho\ \text{div}_x\ v=0\ \ \ \mbox{(conservation of mass)}.
\]
Assume the gas is compressible and that there is a function (state equation)
$$
p=p(\rho),
\]
where \(p'(\rho)>0\) if \(\rho>0\). Then the above system of four equations is
\begin{eqnarray}
\label{euler}\tag{3.3.1.5}
v_t+(v\cdot\nabla)v+\frac{1}{\rho}p'(\rho)\nabla\rho&=&f\\
\label{cont}\tag{3.3.1.6}
\rho_t+ \rho\ \text{div}\ v+v\cdot\nabla\rho&=&0,
\end{eqnarray}
where \(\nabla\equiv\nabla_x\) and \(\text{div}\equiv\text{div}_x\), i. e., these operators apply on the spatial variables only.
The characteristic differential equation is here
$$
\left|\begin{array}{cccc}
\frac{d\chi}{dt}&0&0&\frac{1}{\rho}p'\chi_{x_1}\\
0&\frac{d\chi}{dt}&0&\frac{1}{\rho}p'\chi_{x_2}\\
0&0&\frac{d\chi}{dt}&\frac{1}{\rho}p'\chi_{x_3}\\
\rho\chi_{x_1}& \rho\chi_{x_2}&\rho\chi_{x_3}&\frac{d\chi}{dt}
\end{array}\right|=0,
\]
where
$$\dfrac{d\chi}{dt}:=\chi_t+(\nabla_x\chi)\cdot v. \]
Evaluating the determinant, we get the characteristic differential equation
\begin{equation}
\label{chargas}\tag{3.3.1.7}
\left(\frac{d\chi}{dt}\right)^2\left(\left(\frac{d\chi}{dt}\right)^2-p'(\rho)|\nabla_x\chi|^2\right)=0.
\end{equation}
This equation implies consequences for the speed of the characteristic surfaces as the following consideration shows.
Consider a family \(\mathcal{S}(t)\) of surfaces in \(\mathbb{R}^3\) defined by \(\chi(x,t)=c\), where
\(x\in\mathbb{R}^3 \) and \(c\) is a fixed constant. As usually, we assume that \(\nabla_x\chi\not=0\).
One of the two normals on \(\mathcal{S}(t)\) at a point of the surface \(\mathcal{S}(t)\) is given by, see an exercise,
\begin{equation}
\label{surfnormal}\tag{3.3.1.8}
{\bf n}=\frac{\nabla_x\chi}{|\nabla_x\chi|}.
\end{equation}
Let \(Q_0\in\mathcal{S}(t_0)\) and let \(Q_1\in\mathcal{S}(t_1)\) be a point on the line defined by \(Q_0+s{\bf n}\), where \({\bf n}\) is the normal (\ref{surfnormal}) on \(\mathcal{S}(t_0)\) at \(Q_0\) and \(t_0<t_1\), \(t_1-t_0\) small, see Figure 3.3.1.2.
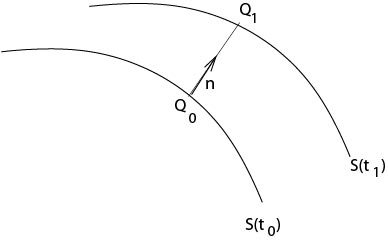
3.3.1.2: Definition of the speed of a surface
Definition. The limit
$$
P=\lim_{t_1\to t_0}\frac{|Q_1-Q_0|}{t_1-t_0}
$$
is called speed of the surface \(\mathcal{S}(t)\).
Proposition 3.2. The speed of the surface \(\mathcal{S}(t)\) is
\begin{equation}
\label{speedsurf}
P=-\frac{\chi_t}{|\nabla_x\chi|}.
\end{equation}
Proof. The proof follows from \(\chi(Q_0,t_0)=0\) and \(\chi(Q_0+d{\bf n},t_0+\triangle t)=0\), where \(d=|Q_1-Q_0|\) and \(\triangle t=t_1-t_0\).
\(\Box\)
Set \(v_n:=v\cdot{\bf n}\) which is the component of the velocity vector in direction \({\bf n}\).
From ({\ref{surfnormal}) we get
$$
v_n=\frac{1}{|\nabla_x\chi|}v\cdot \nabla_x\chi.
\]
Definition. \(V:=P-v_n\), the difference of the speed of the surface and the speed of liquid particles, is called relative speed.
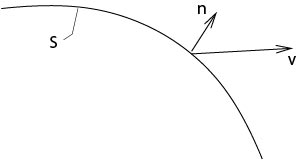
Figure 3.3.1.3: Definition of relative speed
Using the above formulas for \(P\) and \(v_n\) it follows
$$
V=P-v_n=-\frac{\chi_t}{|\nabla_x\chi|}-\frac{v\cdot\nabla_x\chi}{|\nabla_x\chi|}=-\frac{1}{|\nabla_x\chi|}\frac{d\chi}{dt}.
$$
Then, we obtain from the characteristic equation (\ref{chargas}) that
$$
V^2|\nabla_x\chi|^2\left(V^2|\nabla_x\chi|^2-p'(\rho)|\nabla_x\chi|^2\right)=0.
$$
An interesting conclusion is that there are two relative speeds: \(V=0\) or \(V^2=p'(\rho)\).
Definition. \(\sqrt{p'(\rho)}\) is called speed of sound.
Contributors and Attributions
Integrated by Justin Marshall.


