9.6: Center of Mass

Suppose a beam is 10 meters long, and that there are three weights on the beam: a 10 kilogram weight 3 meters from the left end, a 5 kilogram weight 6 meters from the left end, and a 4 kilogram weight 8 meters from the left end. Where should a fulcrum be placed so that the beam balances? Let's assign a scale to the beam, from 0 at the left end to 10 at the right, so that we can denote locations on the beam simply as coordinates; the weights are at , , and , as in Figure 9.6.1.

Figure 9.6.1. A beam with three masses.

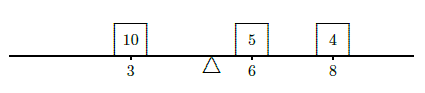
Suppose to begin with that the fulcrum is placed at . What will happen? Each weight applies a force to the beam that tends to rotate it around the fulcrum; this effect is measured by a quantity called torque, proportional to the mass times the distance from the fulcrum. Of course, weights on different sides of the fulcrum rotate the beam in opposite directions. We can distinguish this by using a signed distance in the formula for torque. So with the fulcrum at 5, the torques induced by the three weights will be proportional to , , and .

For the beam to balance, the sum of the torques must be zero; since the sum is , the beam rotates counter-clockwise, and to get the beam to balance we need to move the fulcrum to the left. To calculate exactly where the fulcrum should be, we let denote the location of the fulcrum when the beam is in balance. The total torque on the beam is then

Since the beam balances at it must be that

or

That is, the fulcrum should be placed at to balance the beam.

Now suppose that we have a beam with varying density---some portions of the beam contain more mass than other portions of the same size. We want to figure out where to put the fulcrum so that the beam balances.

The denominator of this fraction has a very familiar interpretation. Consider one term of the sum in the denominator: . This is the density near times a short length, , which in other words is approximately the mass of the beam between and . When we add these up we get approximately the mass of the beam.

Now each of the sums in the fraction has the right form to turn into an integral, which in turn gives us the exact value of :

The numerator of this fraction is called the moment of the system around zero:

and the denominator is the mass of the beam:

and the balance point, officially called the center of mass, is

It should be apparent that there was nothing special about the density function or the length of the beam, or even that the left end of the beam is at the origin. In general, if the density of the beam is and the beam covers the interval , the moment of the beam around zero is

and the total mass of the beam is

and the center of mass is at

Center of mass for a two dimensional plate.

Contributors

David Guichard (Whitman College)

• Integrated by Justin Marshall.