14.6: Orthogonal Complements
- Page ID
- 2090
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Let \(U\) and \(V\) be subspaces of a vector space \(W\). In review exercise 6 you are asked to show that \(U\cap V\) is a subspace of \(W\), and that \(U\cup V\) is not a subspace. However, \(span (U\cup V)\) is certainly a subspace, since the span of \(\textit{any}\) subset of a vector space is a subspace. Notice that all elements of \(span (U\cup V)\) take the form \(u+v\) with \(u\in U\) and \(v\in V\). We call the subspace \(U+V:=span (U\cup V) = \{u+v | u\in U, v\in V \}\) the \(\textit{sum}\) of \(U\) and \(V\). Here, we are not adding vectors, but vector spaces to produce a new vector space!
Definition: Direct sum
Given two subspaces \(U\) and \(V\) of a space \(W\) such that $$U\cap V=\{0_{W}\}\, ,$$ the \(\textit{direct sum}\) of \(U\) and \(V\) is defined as:
\[ U \oplus V = span (U\cup V)= \{u+v | u\in U, v\in V \}. \]
Remark: When \(U\cap V= \{0_{W}\}\), \(U+V=U\oplus V\).
The direct sum has a very nice property:
Theorem
If \(w\in U\oplus V\) then the expression \(w=u+v\) is unique. That is, there is only one way to write \(w\) as the sum of a vector in \(U\) and a vector in \(V\).
Proof
Suppose that \(u+v=u'+v'\), with \(u,u'\in U\), and \(v,v' \in V\). Then we could express \(0=(u-u')+(v-v')\). Then \((u-u')=-(v-v')\). Since \(U\) and \(V\) are subspaces, we have \((u-u')\in U\) and \(-(v-v')\in V\). But since these elements are equal, we also have \((u-u')\in V\). Since \(U\cap V=\{0\}\), then \((u-u')=0\). Similarly, \((v-v')=0\). Therefore \(u=u'\) and \(v=v'\), proving the theorem.
Given a subspace \(U\) in \(W\), how can we write \(W\) as the direct sum of \(U\) and \(\textit{something}\)? There is not a unique answer to this question as can be seen from this picture of subspaces in \(W=\mathbb{R}^{3}\):
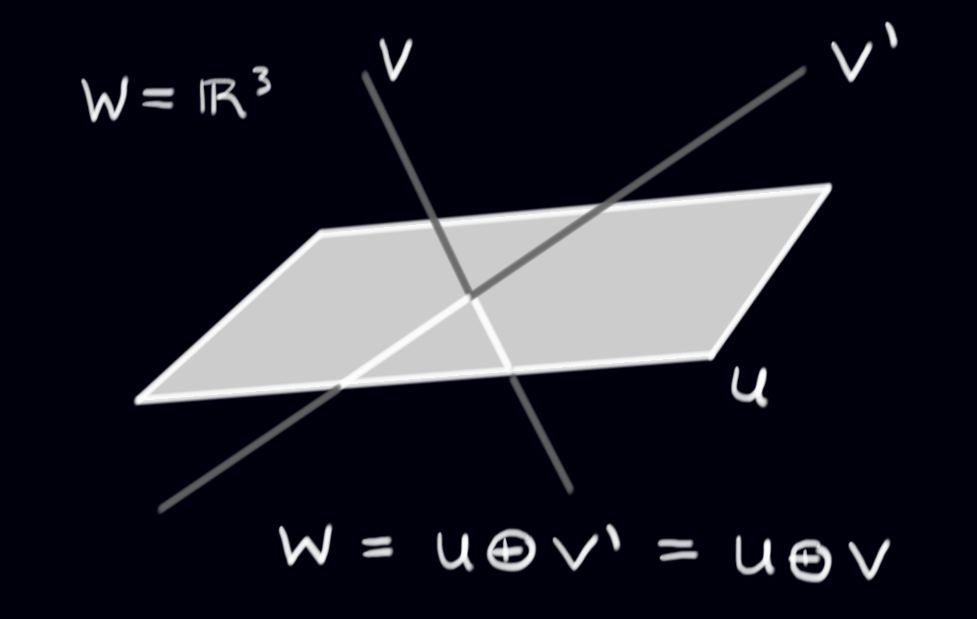
\(\square\)
The general definition is as follows:
Definition
Given a subspace \(U\) of a vector space \(W\), define \(U^{\perp} = \big\{w\in W | w\cdot u=0 \textit{ for all } u\in U\big\}\, .\)}
Remark: The set \(U^{\perp}\) (pronounced "\(U\)-perp'') is the set of all vectors in \(W\) orthogonal to \(\textit{every}\) vector in \(U\). This is also often called the orthogonal complement of \(U\).
Example \(\PageIndex{1}\):
Consider any plane \(P\) through the origin in \(\Re^{3}\). Then \(P\) is a subspace, and \(P^{\perp}\) is the line through the origin orthogonal to \(P\). For example, if \(P\) is the \(xy\)-plane, then
\[ \Re^{3}=P\oplus P^{\perp}=\{(x,y,0)| x,y\in \Re \} \oplus \{(0,0,z)| z\in \Re \}.\]
Theorem
Let \(U\) be a subspace of a finite-dimensional vector space \(W\). Then the set \(U^{\perp}\) is a subspace of \(W\), and \(W=U\oplus U^{\perp}\).
Proof
First, to see that \(U^{\perp}\) is a subspace, we only need to check closure, which requires a simple check: Suppose \(v,w\in U^{\perp}\), then we know
\[v\cdot u = 0 = w\cdot u \quad (\forall u\in U)\, .\]
Hence
\[\Rightarrow u\cdot(\alpha v+\beta w)= \alpha u\cdot v + \beta u\cdot w =0\quad (\forall u\in U)\, ,$$
and so \(\alpha v+\beta w\in U^{\perp}\).
Next, to form a direct sum between \(U\) and \(U\perp\) we need to show that \(U\cap U^{\perp}=\{0\}\). This holds because if \(u\in U\) and \(u\in U^{\perp}\) it follows that
\[u\cdot u = 0 \Leftrightarrow u=0.\]
Finally, we show that any vector \(w\in W\) is in \(U\oplus U^{\perp}\). (This is where we use the assumption that \(W\) is finite-dimensional.) Let \(e_{1}, \ldots, e_{n}\) be an orthonormal basis for \(W\). Set:
\begin{eqnarray*}
u\ &=&(w\cdot e_{1})e_{1} + \cdots + (w\cdot e_{n})e_{n} \in U\, ,\\
u^{\perp}&=& w-u\, .
\end{eqnarray*}
It is easy to check that \(u^{\perp} \in U^{\perp}\) (see the Gram-Schmidt procedure). Then \(w=u+u^{\perp}\), so \(w\in U\oplus U^{\perp}\), and we are done.
\(\square\)
Example \(\PageIndex{1}\):
Consider any line \(L\) through the origin in \(\Re^{4}\). Then \(L\) is a subspace, and \(L^{\perp}\) is a \(3\)-dimensional subspace orthogonal to \(L\). For example, let \(L=span \{ (1,1,1,1)\}\) be a line in \(\Re^{4}.\) Then \(L^{\perp}\) is given by
\begin{eqnarray*}
L^{\perp}&=&\{(x,y,z,w) \mid x,y,z,w \in \Re \textit{ and } (x,y,z,w) \cdot (1,1,1,1)=0\} \\
&=&\{(x,y,z,w) \mid x,y,z,w \in \Re \textit{ and } x,y,z,w=0\}.
\end{eqnarray*}
It is easy to check that
\[
\left\{
v_{1}=\begin{pmatrix}1\\-1\\0\\0\end{pmatrix}, v_{2}=\begin{pmatrix}1\\0\\-1\\0\end{pmatrix}, v_{3}=\begin{pmatrix}1\\0\\0\\-1\end{pmatrix} \right \}\, ,
$$
forms a basis for \(L^{\perp}\). We use Gram-Schmidt to find an orthogonal basis for \(L^{\perp}\):
First, we set \(v_{1}^{\perp}=v_{1}\). Then
\begin{eqnarray*}
v_{2}^{\perp}&=&\begin{pmatrix}1\\0\\-1\\0\end{pmatrix}-\frac{1}{2}\begin{pmatrix}1\\-1\\0\\0\end{pmatrix}
=\begin{pmatrix}\frac{1}{2}\\ \frac{1}{2} \\-1\\ 0 \end{pmatrix},\\
v_{3}^{\perp}&=&\begin{pmatrix} 1\\0\\0\\-1\end{pmatrix} -\frac{1}{2}\begin{pmatrix}1\\-1\\0\\0\end{pmatrix}-\frac{1/2}{3/2}
\begin{pmatrix} \frac{1}{2}\\ \frac{1}{2}\\-1\\0\end{pmatrix} =\begin{pmatrix} \frac{1}{3}\\\frac{1}{3}\\\frac{1}{3}\\-1\end{pmatrix}.
\end{eqnarray*}
So the set \[\left\{ (1,-1,0,0), \left(\frac{1}{2},\frac{1}{2},-1,0\right), \left(\frac{1}{3},\frac{1}{3},\frac{1}{3},-1\right) \right\} \] is an orthogonal basis for \(L^{\perp}\). We find an orthonormal basis for \(L^{\perp}\) by dividing each basis vector by its length:
\[
\left\{
\left( \frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}},0,0 \right),
\left( \frac{1}{\sqrt{6}}, \frac{1}{\sqrt{6}}, -\frac{2}{\sqrt{6}},0 \right),
\left( \frac{\sqrt{3}}{6}, \frac{\sqrt{3}}{6}, \frac{\sqrt{3}}{6}, -\frac{\sqrt{3}}{2} \right)
\right\}.
\]
Moreover, we have
\[Re^{4}=L \oplus L^{\perp} = \{(c,c,c,c) \mid c \in \Re\} \oplus \{(x,y,z,w) \mid x,y,z,w \in \Re,\, x+y+z+w=0\}.\]
Notice that for any subspace \(U\), the subspace \((U^{\perp})^{\perp}\) is just \(U\) again. As such, \(\perp\) is an \(\textit{involution}\) on the set of subspaces of a vector space. (An involution is any mathematical operation which performed twice does nothing.)
Contributor
David Cherney, Tom Denton, and Andrew Waldron (UC Davis)


