part0005

CHAPTER 9. THE INTEGRAL b. Write a formula for

t n dt, valid for n = 1, 2, 3, • • •

Figure for Exercise 9.4.1 Area formulas established in Section {

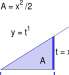
t = x

A = x 3 /3

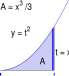
t = x

A = x74

t = x

Exercise 9.4.2 Use Equation 9.17 in Exercise 9.4.1, to compute

a.

t 2 dt b. T t 2 dt c. / ~ t 2 dt

io Jo Jl

Exercise 9.4.3 Use Equation 9.17 in Exercise 9.4.1, to compute

-1 n2

a. J tdt b. J tdt

Exercise 9.4.4 Use Equation 9.17 in Exercise 9.4.1, to compute

a. J t 3 dt b. J t 3 dt

Exercise 9.4.5 Use Equation 9.17 in Exercise 9.4.1, to compute

A. J 3 dt B. J* 3 dt

Exercise 9.4.6 Approximate

A. f 1 e* dt B. P sin(t) dt Jo Jo

using the approximating sum in Definition 9.4.1 and 10 equal subintervals.

Exercise 9.4.7 Use Definition of Integral II to evaluate

r2 1

i r

dt.

Partition [1,2] in n equal subintervals by

n

Let

^o — 1? t\

k – 1 k

tk-i — H , t k — 1 H—,

n n

tk-i x tk, k — 1, 2,

n

CHAPTER 9. THE INTEGRAL

439

a. Show that t k -i < r k < t k .

b. Write Equation 9.16,

rb

f(t)dt = lim

J v ‘ IIAII^n

fc=l

rb n

/ /(*) dt = lim J2 f( T k) x ~ t k -i):

2 1

f° r Ji 72 dt, the given partition and values of r k . c. Show that

f 2 1

/ -7j dt = lim

4.

d. Write the previous sum in long form and show that

2 1 , , / 1\ 1 dt = lim 1 —

i t 2 “‘ ||A|Po V 27 2

Exercise 9.4.8 Use steps similar to those of Exercise 9.18 to show that for x > 1,

i;

■ -2 =1 ~-

h r x

Exercise 9.4.9 You will use this exercise in your proof of the Fundamental Theorem of Calculus, Theorem 10.2.1. Suppose /, is a continuous defined on an interval [a, b] and (v,f(v)) is a high point of / on [a, b] (meaning that v is in [a, b] and for all x in [a, b], f(x) < f(v)).

a. Argue that every approximating sum for f(x) dx is less than or equal to f(v) x (b — a).

b. Argue that

rb

f(x) dx < f(v) x (b — a)

c. Argue that if (u, f(u) is a low point of / on [a, b], then f(u) x (b — a) < J a 6 f(x) dx.

Exercise 9.4.10 In previous sections, values of the following integrals were given. What are they?

r 1 1 r 2 1

A. / dt = B. / -dt =

Jo 1 + t 2 Ji t

Exercise 9.4.11 Write an integral that is the area of the region bounded by the graphs of

a. y = t 2 —t and y — 0, t — 1, t = 2.

b. y — t 2 , and y — t, t — 1, t = 2.

c. y = t 2 , and y — t, t = 0, t — 1.

d. y = 2 x t 5 – t 4 , and y = 0, t = 1, t = 2.

e. y = 2 x t 5 , and y = t 4 , t = 1, t = 2.

It is useful to sketch the regions.

Exercise 9.4.12 Suppose a particle moves with a velocity, v(t) =

CHAPTER 9. THE INTEGRAL

440

b. Write an integral that is the distance moved by the particle between times t — — 1 and t — 1.

Exercise 9.4.13 Suppose an item is drawn from a normal distribution that has mean 0 and standard deviation 1 (p(x) = e~ x I 2 ). Write an integral for the probability that the item is

a. less than one standard deviation from the mean.

b. less than two standard deviations from the mean.

Exercise 9.4.14 Suppose water is flowing into a barrel at the rate of R(t) = 1 + t 2 m 3 /min for 0 < t < 3 minutes. Write an integral that is the volume of water put into the tank. Confirm that the units on the integral are volume.

Exercise 9.4.15 Water flows into a tank at the rate of R(t) = 1 + 1 2 /5 m 3 /min for 0 < t < 3 minutes and the concentration of salt in the water is C(t) = 3.5e~* g/1 at time t. Write an integral that is the total amount of salt that flowed into the tank. Confirm that the units on the integral are grams of salt.

Exercise 9.4.16 Write an integral that is the work done in compressing a syringe of stroke 10cm and radius of 1cm from 10 to 5 cm. Confirm that the units on the integral are of units of work.

Exercise 9.4.17 What is the norm of the partition {0.0,0.2, 0.3, 0.6, 0.7, 0.9,1.0} of [0,1]? Write a partition of [0,1] whose norm is 0.15.

Exercise 9.4.18 Write an approximating sum to the given integrals for the partition {0.0, 0.2, 0.3, 0.6, 0.7,0.9,1.0} of [0,1].

a. / 1 dx d. x 2 dx

Jo Jo

c. / e x dx d. / sin(7ra;) dx Jo Jo

Exercise 9.4.19 Average value of a function. The average value of a function / on an interval [a, b] is defined to be

1 r b

Average value of / on [a, b] / f(t)dt. (9.19)

b — a J a

Use the approximating sum in Definition 9.4.1 and explain why

1 n

— y

( b-a\ b-a f \ a + k x x

n J n

is a reasonable approximation to the average value of / on [a, b].

Exercise 9.4.20 Write the average solar intensity over a year for Eugene, Oregon in integral form. Assume that solar intensity is measured continuously 24 hours per day. See Exercise 9.1.3

Exercise 9.4.21 Let x be a number in [0, |]. Use the trigonometric identity

± eos(fcx 0) = ^±^h^M and lim SinW =1 tl 2sin(f) »-» h

to compute from Definition I the integral

rx

cos(i) dt = sinx

Jo

CHAPTER 9. THE INTEGRAL

9.5 Properties of the integral.

441

Property 9.5.1 Linearity of the integral. Suppose / and g are integrable functions defined on an interval [a, b] and c is a number. Then

A. [ b [f(t)+g(t)]dt = f f(t)dt+ I* g(t)dt (9.20)

J a J a J a

B. f cxf(t)dt = cx I* f(t)dt (9.21)

J a J a

The linearity properties are intuitive. If / is the rate of production of urea and g is the rate of production of creatinine, then / + g is the rate of production of nitrogenous waste products. The total production of nitrogenous waste products (f a (f(t) + g(t))dt) is the sum of the total production of urea (/* f(t)dt) and the total production of creatinine (f^g(t)dt). If the rate of production of urea is changed by a factor of c, then the total production of urea (J a b c x f(t)dt) is c times the previous production of urea (c f% f(t)dt).

The word linear is associated with these two properties, because linear functions of the form P(x) = m x x have the properties.

P(x + y) = mx(x + y)=mxx + mxy = P(x) + P(y) P(c x x) = m x (cx x) = cx (m x x) = cx P(x)

The sine function is not linear, despite the efforts of many students. For most values of x and y

sin(x + y) 7^ sin(x) + sin(y).

Compare this with the trigonometric identity

sin(x + y) — sm(x) cos(y) + cos(a;) sin(?/)

The reasons the integral has the two linearity properties is that the approximating sum also has the two properties. The integral being the limit of the approximating sums inherits the linearity properties of the approximating sums. For example, if / and g are functions defined on an interval [a, b] and c is a number, and a = t 0 < ti < t 2 ■ ■ ■ < t n -i < t n = b is a partition of [a, b] and

to<T~i<ti ti<T 2 <t 2 ■■■ tk-l<Tk<tk ■■■ t n ^i<T n <t n

then

A. £2=1 [/(Tfe) + g(n)] x (t k – i fe -i) = ELi fin) x (t k – tk-i) + £2=i g(r k ) x (t k – t k -i),

B. £fc=i c x f( T k) x (t k – i fe -i) = c££ =1 f(r k ) x (t k – t k -!).

Each approximating sum for f(t) + g(t) dt is the sum of approximating sums for f% f(t) dt and fa 9(t) tit, and each approximating sum for cx f(t) dt is c times an approximating sum for

Iaf(t)dt.

CHAPTER 9. THE INTEGRAL

442

Example 9.5.1 Compute

A.

t 2 + t

dt

B f

Jo

2xtdt

Solution: A. By Equation 9.17 in Exercise 9.4.1, Jq t 2 dt = |, and /J tdt — \. From Property 9.5.1 A,

f 1 It 2 +t] dt= f 1 t 2 dt + f 1

JO 1 J JO JO

* 2 *+ ‘ <*=3+2=6

f-2 r2

2tdt = 2x tdt = 2×2 = 4

B. By By Equation 9.17 in Exercise 9.4.1, J 2 tdt = 2. From Property 9.5.1 B

f 2 2t dt = 2 x f 2 Jo Jo

Although many students think otherwise, it is not always (or even usually) true that

f [fit) x g{t)} dt = f f\t) dt x f git) dt Almost Never True!

J a J a J a

For example, let f(t) = t 2 and g(t) = t. Then

J 2 fit) x git) dt = J 2 t 2 xtdt = J 2 t 3 dt ‘”

but

f(t)dt) x

git) dt

2 t 2 dt] x ( f 2 tdt

4 ‘

37 \2J T 4

Also, it is not always true (and it is not even usually true) that

a git)

f(t)dt

f g(t)dt

J a

2 «’) *

but

i g(t)

J 2 fit) dt J’t

Almost Never True!

2 t , f 2 , 3

— dt = tdt — -, it A 2′

2 S

_ 3 _ 16 / 3 ~ “3 ~Y^2′

Three more properties of the integral are: Property 9.5.2 Geometry of the integral.

1. Suppose / is an integrable function defined on an interval [a, b] and c is a number between a and b. Then

f C f(t)dt+ f f(t)dt= f b f(t)dt (9.22)

J a J c J a

2. Suppose / and g are integrable functions defined on an interval [a, b] and for all t in [a, b], fit) < git). Then

f f(t)dt< f” g(t)dt (9.23)

Ja J a

CHAPTER 9. THE INTEGRAL

443

A

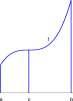
B

C

Figure 9.15: A. (Left) / a c /(£) dt + / c 6 /(t) dt = J a 6 /(t) dt. B. (Center) The area under the graph of / is < the area under the graph of g. C. (Right) The area under the graph of / equals the area under the graph of g, where g(t) = f(t — c).

3. Suppose / is an integrable function defined on [a, b], and c is a number. Then

[ b+C f(t-c)dt= [ b f(t)dt (9.24)

J a+c J a

We refer to these as geometric properties because they are so obvious from the area interpretation of the integral. In Figure 9.15 A, it is clear that the area under the graph of / between t = a and t = b is the sum of the area between t = a and t = c and the area between t = c and t = b. In Figure 9.15, B, it is clear that the area under the graph of / is less than the area under the graph of g. In Figure 9.15, C, the region below the graph of g(t) = f(t — c) is a simple translation of the region under the graph of / and the areas are equal. Formal proofs of the properties based on approximating sums can be given, but the geometry alone is convincing, and we omit the formal proofs. Your solution to Explore 9.5.1 will give you some algebraic insight to the properties.

Explore 9.5.1 Remember from Definition 9.4.3 that an approximating sum for the integral of / on [a, b] is a number of the form

fin) x fa – t 0 ) + f(r 2 ) x (t 2 – t x ) + ■ • • + f(r k ) x (t k – t k _ x ) + ■■■ + f(r n ) x (t n – t n ^).

Suppose / and g are continuous increasing functions defined on an interval [a, b] and for every t in [a, b], f(t) < g(t) and suppose that c is a number.

a. Show that every approximating sum of J a f(t) dt is less than or equal to some approximating sum of g(t) dt.

b. Show that every approximating sum to f£ fit) dt is equal to an approximating sum to

c. Show that if a < c < b and S afi is an approximating sum for f£ f(t) dt and S Cj b is an approximating sum for J c b f(t) dt, then S a , c + <Sc,& is an approximating sum for f£ f(t) dt.

Explore 9.5.2 Which of properties 9.5.2 is illustrated by the following statements?

CHAPTER 9. THE INTEGRAL

444

a. John measures the rain fall from 2 to 4 pm and Jane measures the rain fall from 1400 to 1600 hours. They get the same amount.

b. If Jane runs faster than John, Jane will go farther than John.

c. The total damage done by the insects includes the damage done during the larval, pupal, and fully emerged insect stages.

Explore 9.5.3 Decide on a reasonable value for

f(t)dt

(9.25)

and give a geometric argument for your answer.

9.5.1 Negatives.

It has been assumed that in the symbol, f% f(x) dx, a < b. There are instances when one wants to extend the integral concept to the case b < a and even the case a = b. This is done by

Definition 9.5.1 Suppose / is an integrable function defined on [a, b}. Then

f a f(t) dt = – f f(t) dt and f f{t) dt = 0

J b J a J a

It has been implicit in much of the discussion that f(x) is positive for all x in [a, b}. This is not required, and a number of instances suggest using functions with negative values.

Example 9.5.2 For example, a ball thrown vertically may have a positive velocity as it ascends, but will then have a negative velocity as it descends. If one throws the ball with a vertical velocity of 19.6m/s, then the velocity t seconds later will be 19.6 — 9.8tm/s where the term 9.8£ is the change in velocity due to gravity. A graph of the velocity is shown in Figure 9.16.

2 3

Figure 9.16: Velocity of a ball thrown vertically, v(t) = 19.6 — 9.81

At t = 2 seconds the velocity is zero, the ball is at its maximum height, and that height is the area of the triangle marked ‘+’ in Figure 9.16. Between t = 2 and t = 4 seconds the velocity is negative, the motion of the ball is downward and the displacement is the area of the triangle marked ‘-‘ in Figure 9.16. At t = 4 the ball has fallen to its original starting point. The net displacement is zero and that is J 0 v(t) dt, the sum of the ‘areas’ of the two triangles treating the area of the second triangle as negative (see Exercise 9.5.9). The distance traveled by the ball is the sum of the areas of the two triangles, both treated as positive. ■

CHAPTER 9. THE INTEGRAL

445

Exercises for Section 9.5, Properties of the integral. Exercise 9.5.1 Do Explore 9.5.1. Exercise 9.5.2 Do Explore 9.5.2. Exercise 9.5.3 Do Explore 9.5.3.

Exercise 9.5.4 Which of the linear properties of the integral are illustrated by the following

examples?

a. The death rate from cancer is about 2/3’s that of heart disease. In a year’s time 2/3’s as many people die from cancer as die from heart disease.

b. The common cold incidence is 0.348 per person per year and the influenza incidence is 0.254 per person per year. In three years, a town of 10,000 people experienced 18,060 respiratory viral infections.

Exercise 9.5.5 Is the exponential function, E(x) = e x , linear? Prove or disprove. Exercise 9.5.6 Is the logarithm function, L(x) = ln(x), linear? Prove or disprove. Exercise 9.5.7 Compute (note: change x to t if it confuses you.)

a.

3 + x 2

dx

Exercise 9.5.8

a. Compute: Pi

s:

t x r

.4 ^3

b. Compute: Qi ~o dt

J2 t

b.

dt

i:

3x dx

and

and

c. J 3x — 6x dx

s:

tdt x

t 2 dt

Q 2

r 4

/ t 3 dt

J 2 t2dt

c. What do these two problems illustrate?

Exercise 9.5.9 In Example 9.5.2 it was claimed that J 0 4 v(t) dt = J 0 4 (19.6 — 9.8t) dt is the sum of the areas of the two triangles in Figure 9.16. Compute

a. [ 2 (19.6 – 9.8t) dt, b. T (19.6 – Q.St) dt, and c. C (19.6 – 9.8t) dt.

JO J2 JO

Compare your answers with the areas of the triangles in Figure 9.16.

CHAPTER 9. THE INTEGRAL

446

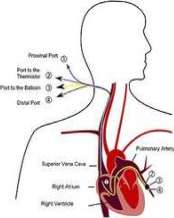
Figure 9.17: Schematic diagram of the heart and a Swan-Ganz catheter threaded throughout the right atrium and into the pulmonary artery, from http://en.wikipedia.org/wiki/Pulmona...rtery_catheter placed by Chikumaya.

9.6 Cardiac Output

The problems of this section are directed to understanding a procedure used for measuring cardiac output. Briefly, the procedure is

Infuse a quantity, Q, of 10°C saline solution into the right side of the heart, and measure the temperature of the fluid in the pulmonary artery exiting from the heart as a function of time, T(t). Then the flow rate is

F = ® m (9.26)

JO 37-10 Ui

Our goal is to understand why Equation 9.26 correctly gives the flow rate. The following material describes the physiology and is copied from R.A. Rhoades and G. A. Tanner, Medical Physiology., Little, Brown and Company, 1995, pp 271-2.

The Thermodilution Method. “In most clinical situations, cardiac output is measured using a variation of the dye dilution method called thermodilution. A Swan-Ganz catheter (a soft, flow-directed catheter with a balloon at the tip) is placed into a large vein and threaded through the right atrium and ventricle so that its tip lies in the pulmonary artery. The catheter is designed so a known amount of 10°C saline solution can be injected into the right side of the heart via a side pore in the catheter. This solution decreases the temperature of the surrounding blood. The magnitude of the decrease in temperature depends on the volume of blood that mixes with the solution, which depends on cardiac output. A thermistor on the catheter tip (located downstream in the pulmonary artery) measures the fall in blood temperature. Using calculations similar to the dye dilution method, the cardiac output can be determined.”

CHAPTER 9. THE INTEGRAL

447

Measurement of cardiac output as just described is a common procedure in hospitals. Patients returning from cardiac surgery have a Swan-Ganz catheter inserted as described. Measurements of cardiac output may be made hourly for the first 24 hours, followed by measurements every 2 hours for the next two days. You will find the web site of a catheter manufacturer, Edwards Lifesciences, interesting.

A useful first step in understanding Equation 9.26 is to check the units on the left and right hand side. The units on the integral are the same as the units on the approximating sums for the integral.

It is reasonable to assume that the flow rate, F, is measured in ml/sec so that the right hand side should also have units of ml/sec. The quantity, Q, should be measured in ml. A general approximating sum for the integral in the denominator is

y 37 – T(t k ) tx 37-10

The fraction 37 3 ~ T [ < 0 fc > is the ratio of temperatures, and is therefore dimensionless. The factor (tk ~ tk-i) is measured in seconds, so that the unit on the approximating sum is seconds, as is the unit on the integral. Therefore the units on both sides of Equation 9.26 are ml/sec. In order to understand the Equation 9.26 it is necessary to understand “The magnitude of the decrease in temperature depends on the volume of blood that mixes with the solution, which depends on cardiac output. “

and the next few examples and exercises are directed to that end.

Example 9.6.1 Suppose 10 ml of 9°C water is mixed with 60 ml of 37° C water. What will be the temperature of the mixture?

We base our answer on the concept of heat content in the fluids measured with a base of zero heat content at 0 °C. It is helpful for this example that the specific heat of water is 1 calorie per gram-degree C. The definition of a calorie is the amount of heat required to raise one gram of water one degree centigrade — specifically from 14.5 to 15.5 degrees centigrade, but we will assume it is constant over the range 0 to 37 degrees centigrade.

The following table is helpful:

Vol (ml) Temp (°C) Calories

Fluid 1 10 9 10 x 9 = 90

Fluid 2 60 37 60 x 37 = 2220

Mixture 70 T 70 x T

The critical step now is the conservation of energy. The calories in the mixture should be the sum of the calories in the two fluids (we assume there is no heat of mixing) so that

70 x T = 90 + 2220 T = 33°C ■

Care must be taken when mixing two fluids of different heat capacities. If 10 ml of 9°C cream is mixed with 60 ml of 37°C coffee, the temperature of the mixture would be slightly more than 33° because the specific heat of cream is 0.9 cal/ml °C and the specific heat of coffee is approximately that of water, 1.0 cal/ml °C.

Explore 9.6.1 Show that the temperature of mixture of 10 ml of 9°C cream and 60 ml of 37°C coffee would be approximately 33.35°C.

Suppose Vi ml of fluid 1 at temperature Ti and specific heat C\ cal/ml are mixed with v 2 ml of fluid 2 at temperature T 2 and specific heat C 2 cal/ml. The temperature of the mixture will be

_ v 1 C 1 T l + v 2 C 2 T 2

J-mixture /~i W ‘ J

viCi + v 2 C 2

We now turn to the problem of measuring cardiac output. Suppose Q ml of 10°C saline solution are infused into the right side of the heart and the temperature T(t) in the pulmonary artery is measured. Assume that the heat capacity of saline solution is the same as the heat capacity of blood and that flow rate past the thermometer is a constant, F. The concentration of saline solution at the thermometer is

= 37-TW W 37-10

The amount of saline solution that passes the thermometer in time interval [0,£i] is

37 – T{t) ^ r ^ 37 – T(t)

/ 1 Fx K(t) dt = f 1 Fx ‘ }J dt = Fx [ Jo w Jo 37 -10 Jo

dt. 37-10

Consider t\ to mark the end of measurement and label it as oo. Then the amount of saline solution that passes the thermometer must also be Q, the amount injected. We can write

Jo

dt 37-10

Exercises for Section 9.6, Cardiac Output. Exercise 9.6.1 Compute the units on the right side of Equation 9.27.

Exercise 9.6.2 Suppose 10°C saline solution is mixed with 50 ml of 37°C blood and the mixture is 35°C. How much saline solution was added? Assume equal heat capacities.

Exercise 9.6.3 Suppose 10°C saline solution is mixed with 25 ml of 37°C blood and the mixture is 32°C. How much saline solution was added? What is the concentration of saline solution in the total of the two fluids? Assume equal heat capacities.

Exercise 9.6.4 In Equation 9.27, assume that C\ = C 2 and let K = — v _£ — be the concentration of the second fluid in the total of the two fluids (we will think of blood as the first fluid and saline solution as the second fluid) and Temp be the temperature of the mixture. Show that

K = Ti- Temp Tx-T 2

Exercise 9.6.5 Fill in the blank entries in Table 9.6.5. Assume the heat capacities of blood and saline solutions are equal.

(9.28)

CHAPTER 9. THE INTEGRAL

449

Table for Exercise 9.6.5 ARTIFICIAL DATA. GET REAL DATA FROM SWAN-GANZ CATHETER COMPANY. Fluid Temperature in the pulmonary artery after injection of 10 ml of

10°C saline solution in the right side of the heart.

Exercise 9.6.6 Based on the data in Table 9.6.5, if the heart flow rate is R ml/sec, how much saline solution passed the thermometer downstream of the heart during the time interval [0, 20] sec?

Exercise 9.6.7 From the data in Table 9.6.5, what is the cardiac capacity?

Exercise 9.6.8 Seymour S. Kety and Carl F. Schmidt 7 described a widely acknowledged and accurate method for determination of cerebral blood flow, and subsequent measurement of cerebral physiological activity such as cerebral rate of oxygen metabolism. It is commonly referred to as the Kety-Schmidt technique, and has the following outline:

1. An inert substance, a, is introduced into the blood (patient breathes 15% N2O or 133 Xe dissolved in saline is infused into the axillary vein, and other similar methods).

2. At times, t, after the start of administration, the arterial concentration, A(t), of o is measured in the radial artery.

3. The venous concentration, V(t), of a is measured at the base of the skull in the superior bulb of the internal jugular, at the point of exit of jugular vein from the brain.

Data read from curves shown in Kety and Schmidt, Ibid, are shown in Table 9.6.8.

Table for Exercise 9.6.8 Data read from Figure 1, on page 476, of C. M. Kety and S. S.

Schmidt, J. Clinical Invest. 27: 476-483, 1948.

7 Kety, S. S, and Schmidt, C. M., The nitrous oxide method for the quantitative determination of cerebral blood flow in Man: Theory, procedure, and normal values, J. Clinical Invest. 27: 476-483, 1948.

CHAPTER 9. THE INTEGRAL

450

Assume a constant cerebral blood flow rate, R, grams/minute, that A(t) is the concentration of N2O (cubic centimeters of N 2 0 per cubic centimeter of blood) in blood flowing into the brain, and that V(t) is the concentration of N 2 0 in blood flowing out of the brain.

a. Using a flow rate, R (an unknown constant, units of cc blood/min), and the data, compute an estimate of the amount of N 2 0 that flowed into the brain during time [0,10] (measured in minutes).

b. Using R and the data, compute an estimate of the amount of N 2 0 that flowed out of the brain during time [0,10].

c. From the previous two steps you should be able to estimate that the amount of N 2 0 accumulated in the brain during time [0,10] is approximately R x 0.0827cc N 2 0.

d. Note that after 10 minutes the venous and arterial concentrations of N 2 0 are about the same, indicating that the brain is essentially saturated. Assume that at 10 minutes the concentration of N 2 0 in the brain is 0.042 ^faain ^ e same as ^(10))> an d compute the total amount of N 2 0 in a brain of 1400 cc 8 .

e. Equate the two estimates of the amount of N 2 0 in the brain and compute R. (600 – 900 gm/min = 600 – 900 ml/minute is normal for an adult; resting cardiac output is 5-6

L/minute.)

f. Describe how knowledge of blood flow and two additional measurements can be used to compute cerebral metabolic uptake of oxygen.

9.7 Chlorophyll energy absorption.

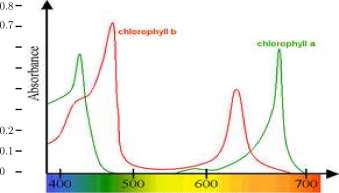
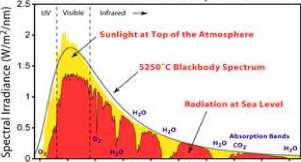
Shown in Figure 9.18 are graphs of the energy absorbance of chlorophylls a and b and Solar Spectral Irradiance in W/m 2 /nm = W/(m 2 x nm). Note nm = nanometer = 10~9 meters.

Question: Which of chlorophyll a or chlorophyll b in leaves captures the most energy?

CHAPTER 9. THE INTEGRAL

451

Table 9.3: Chlorophyll Data read from a magnification of the upper graph in Figure 9.18. The irradiance data is read from a table from the Renewable Resource Data Center that appears in http://rredc.nrel.gov/solar/spectral.../ASTMG173.html and was the basis for the lower graph in Figure 9.18

Consider chlorophyll a. Energy absorbance in Figure 9.18 at a light frequency A is measured by putting into a spectrophotometer a sample of chlorophyll a, dissolved in a solvent (diethyl ether, for example), and measuring light transmission, ItransW, through the sample from a light source I 0 of frequency A, assumed to be constant for all A. Then

Energy Absorbance at A = Absorb{\) = Klog 10 ~rvv- (9.29)

^trans \A)

K is measured in l/(M-cm 2 ) reflects the molar concentration of chlorophyll, M, and thickness of the sample. For the purpose of comparing the two chlorophylls, we assume that K — 1.

We have added a vertical scale to the absorbance graph in Figure 9.18. The lowest value, 0, is consistent with Equation 9.29: when no light is absorbed, Itrans(^) — lo, Iq/ hrans{X) = 1, and log 10 Io/hrans = k>g 10 1 = 0. The largest value of the scale, 0.8, is chosen so that the range of the argument of the logarithm is not too large.

The fraction of I 0 that is absorbed is

Fraction Absorbed(A) = FracAbsorb(X) = J ° – I Jp^l = \ _ m -Absorb(x) ^ ^

FracArsorb has dimension 1 (or is dimensionless).

We partitioned the visible spectrum (400 nm to 700 nm) into intervals with smaller intervals where the graphs change rapidly and measured data shown in Table 9.3 read from magnifications of the graphs in Figure 9.18.

At any light frequency, A, the energy absorbed by chlorophyll a is

Irradiance(A) x FracAbsorb(X)W/ (m 2 x nm),

and for an interval, [p, q] , of frequencies we approximate the energy absorbed in that interval as (think ‘trapezoidal approximation’)

Irradiance(p) x FracAbsorb(p) + Irradiance^) x FracAbsorb(q)

2

For the visible spectrum, [400, 700], we estimate the total absorbance as

(q-p).

^ Irradiance(Aj) x FracAbsorb(Xi) + Irradiance(Aj + i) x FracAbsorb(\i + i) , . 2^ o ‘ +1 ~

CHAPTER 9. THE INTEGRAL

452

Wavelength [nim]

Solar Radiation Spectrum

Sunlight flt Top- af this- Almasphar*

250 500 750 1000 1Z50 1500 17S0 2000 £250 25O0 Wavelength (nm)

Figure 9.18: Upper graph. Energy absorption for chlorophylls a and b. Wikipedia Commons, http://en.wikipedia.org/wiki/File:Ch...ab_spectra.png Nashev and Luis Fernndez Garcia supplied the file and modifications. The vertical scale is added to provide a quantitative comparison between the two graphs. Lower graph. Solar Spectral Radiation W/m 2 /nm at sea level versus light wave length. Provided by Robert A. Rohde (Dragons flight) on Wikipedia, http://en.wikipedia.org/wiki/File:Solar .Spectrum.png.

CHAPTER 9. THE INTEGRAL

453

Wave length, A, is measured in nanometers, so the dimension is W/m 2 . The ultimate answer is

/■700

/ Irradiance(A) Absorbancea(A) d\ W/m 2 .

J400

For chlorophyll a we get 59 W/m 2 . You are asked to compute the total absorbance for chlorophyll b in Exercise ?? You should find that absorbance for chlorophyll b is about 52 percent greater than that for chlorophyll a. This is consistent, at least, with the observation that chlorophyll b is an evolutionary derivative of chlorophyll a.

Exercise 9.7.1 The computer program shown below computes the total absorbance of both chlorophylls. This problem is best if you can copy and run this program on your computer. Note: You can copy from the internet book and paste it in a blank MATLAB program sheet.

a. Interpret the output which is: 58.9849 89.5865 1.5188.

b. Three lines are commented out with %%. Delete the %% in the first two of these lines and interpret the result: 36.3818 55.8938 1.5363.

c. Replace those two %%’s and delete the %% in the third line. Interpret the result: 53.7928 76.5903 1.4238.

d. Delete the %% in each of the three lines and interpret the result: 33.6750 47.9500 1.4239.

c. So far, what can you tell about the question, “Which of chlorophyll a or chlorophyll b in leaves captures the most energy from sunlight?”

f. What additional information would you wish to have in order to give a more certain answer to the previous question?

0 /o°/o Comparisons of Chlorophyll a and Chlorophyll b close all;clc;clear

Lam= [400 420 425 440 460 470 480 500 520 540 560 …

580 600 620 630 640 660 675 680 700]; Chl_a= [0.35 0.47 0.54 0.23 0.03 0.0 0.0 0.0 0.0 0.0 0.01 …

0.03 0.02 0.04 0.05 0.08 0.20 0.58 0.13 0.0]; Chl_b= [0.18 0.33 0.35 0.36 0.53 0.72 0.20 0.04 0.03 0.02 0.03 …

0.04 0.05 0.17 0.39 0.16 0.04 0.02 0.01 0.0]; 1= [0.84 0.88 0.99 1.10 1.28 1.27 1.38 1.34 1.33 1.31 …

1.31 1.35 1.33 1.33 1.26 1.30 1.27 1.26 1.27 1.16];

ZZ = ones(size(Chl_a)); FA_a = ZZ – 10.~(-Chl_a); FA_b = ZZ – 10.~(-Chl_b);

°/„°/„ FA_a = Chl_a; 11 FA_b = Chl_b; U I = ZZ;

CHAPTER 9. THE INTEGRAL

454

plot(Lam,FA_a,’g’,’linewidth’,2); hold(‘on’); plot(Lam,FA_b, ‘r’ ,’linewidth’,2) plot(Lam,FA_a,’gd’,’linewidth’,2); plot(Lam,FA_b,’rs’,’linewidth’,2)

N=length(I); Sum_a =0.0; Sum_b =0.0; for i = 1:N-1

Delta = Lam(i+1) – Lam(i);

Sum_a = Sum_a + 0.5*(I(i)*FA_a(i)+I(i)*FA_a(i+l))*Delta; Sum.b = Sum.b + 0.5*(I(i)*FA_b(i)+I(i)*FA_b(i+l))*(Delta);

end

[Sum.a Sum_b Sum_b/Sum_a]

Exercise 9.7.2 There is a reason why the computer program using FracAbsorb(X) (original program) and Absorbance(A) with the first two %%’s removed) give similar results, including similar graphs. The reason involves the Taylor polynomial

e~ x = 1 — x + —— fracx 3 6 + — where 0 < c < x.

See Exercise 12.7.6.

Exercise 9.7.3 Write an integral that is the energy absorbed by chlorophyll b over the visible spectrum from 400 to 700 nm.

Exercise 9.7.4 Should we also consider possible chlorophyll absorbance of light in the ultra violet range of light wave length (< 400 nm)?

Chapter 10

The Fundamental Theorem of Calculus

Where are we going? You should conclude from the title that this chapter is important.

You have studied the two primitive concepts of calculus, the derivative and the integral. They are based on the notion of limit, but each concept has been defined without reference to the other. The Fundamental Theorem of Calculus defines the relation between the derivative and the integral, and shows that each operation is the inverse of the other. A powerful method of evaluating integrals is a result.

10.1 An Example.

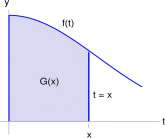
Let A be the function defined by

A(x) = f X sin(t) dt for 0 < x < J Jo 2

Then for x in [0, 7r/2], A(x) is the area of the region bounded by the graphs of y = smt y = 0 and t — x (see Figure 10.1 A). We have two goals. Goal I. Show that for any x, 0 < x < 7r/2, A’ ( x ) = sin(x)

Goal II. Suggest (and it is actually true) that A( x ) = — cos(a;) + 1 for 0 < x < ir/2.

Proof of Goal I, A'{x) = sin(x). We will show that the right hand derivative, ,,,, . , A(x + h) — A(x) . .

A’ + (x) = lim —^ £ ^ = sm(x) for 0 < x < ir/2.

A similar argument shows that the left hand derivative, A’~(x) = sin x for 0 < x < n/2, so that A\x) = sinx on 0 < x < n/2.

CHAPTER

10. THE FUNDAMENTAL THEOREM

OF CALCULUS

456

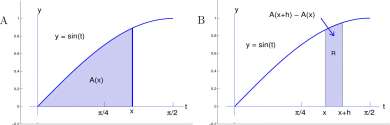
Figure 10.1: A. Area A(x) of region bounded by the graphs of y = sint, y = 0 and t = x. B. Area of region between x and x + h.

Let x and h > 0 be numbers satisfying 0<x<x-\-h<ir/2 and R be the region (shaded in Figure 10. IB) between t = x and t = x + h and below the graph of y = sin(a;) and above y = 0. R is the difference of two regions under the graph of y = sin(x), one between t = 0 and t = x + h and the other between t = 0 and t = x, and

Area of R is A(x + h) – A(x) (10.1)

In Figure 10.2A is a rectangle, R\, that is contained within R and the area of R\ is less than the area of R. The height of R\ is sin(x) and the width is h, so the

Area of R\ is sin(ar) h (10-2)

In Figure 10.2B is a rectangle, i?2, that entirely contains R and the area of R2 is greater than the area of R. The height of R2 is sin(x + h) and the width is h, so the

Area of R2 is sin(x + h) h (10.3)

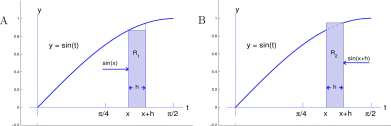
Figure 10.2: A. Rectangle Ri of area (sinx) h. B. Rectangle R 2 of area (sin(x + h)) h. We conclude from

Area of R\ < Area of R < Area of R2

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

457

and from Equations 10.1 to 10.3 that (remember, h > 0)

sin(x) h < A(x + h) — A(x) < sin(x + h) h

■ ( \ / A(x + h) -A(x) ^ • / , m

sin(i) < —^ / ^ < sm(:r + h)

Now

7T

a. b. c.

. , N A(x + h) – A(x) . , , , N

sin(i) < — ^ ^ < sin(i + a)

As /i —^ 0+ | | |

;io.4)

sin(a;) < A’ + (x) < sin(a;)

from which it follows that

7T

A’ + (x) = sin(x) for 0 < x <

The three limits, a., b. and c. in Equation 10.4 are important. Limit a. is valid because sinx is independent of h. Limit b. is the definition of the righthand derivative, A’ + . Limit c. is correct because sinx is continuous at x, which is shown in Exercise 7.1.4.

Our argument has assumed that h > 0 and 0 < x < ir/2. Simple modifications of the argument imply that A’~(x) = sinx for 0 < x < 7r/2. so that A'(x) = sinx for 0 < x < tt/2. The domain of A is [0,7r/2], and by definition A'(0) = A’ + {0) = sinO and A'(ir/2) = A’-(ir/2) = sin tt/2. Goal I has been met.

Argument supporting Goal II, A(x) = — cos(a;) + 1. We know that A'(x) = sin(x). Derivative formulas will yield

[— cos(x)]’ = sin(x).

Thus A(x) and — cos(x) have the same derivative, sin(x). We might think, then, that because A{x) and — cos(x) have the same derivative, they must be the same functions. That is too strong because constant functions have derivative = 0, and, for example,

[— cos(x) + 13]’ = sin(x), also.

But we can conclude (as we will see in Theorem 10.3.2) that there is a number C such that

A(x) = – cos(x) + C

Now A(0) = Jq sintdt = 0, and cos(0) = 1, so

A(0) = -cos(0) + C 0 = -1 + C C = 1

Therefore

A(x) = — cos(x) + 1 Goal II has been met. End of proof Goal I and argument for Goal II.

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

458

We have obtained this formula without reference to approximating sums. This same formula was found in Example 9.4.4 using the limit of approximating sums.

In this chapter we give arguments for more general results, but the stepping stones for all of them are those we have just shown.

10.2 The Fundamental Theorem of Calculus.

Proof of the Fundamental Theorem of Calculus. We prove the theorem for the case that / is increasing. Suppose / is an increasing and continuous function defined on [a, b] and for each x in [a, b], G(x) = f% f(t) dt. We will prove that the right hand derivative

ni+i \ v G(x + h)-G(x) . . . G+(x) = hm — j — = fix) for a < x < b.

A simple modification of the argument shows that G’~(x) = f(x) for a < x < b, so that G'(x) = f(x) for a < x < b.

Proof that G’ + (x) = f(x). Let x and x + h be numbers in [a, b] with h > 0. Refer to Figure

10.3.

A

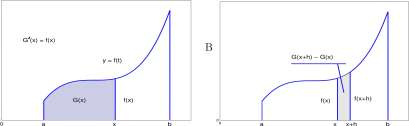
Figure 10.3: A. G(x) = /* f{t) dt. B. G(x + h) – G(x) = f, f(t) dt.

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

459

Explore 10.2.1 Do This. Give reasons for the steps (i), ■ ■ ■ , (viii), below. You will need the results of Exercise 9.4.9, that if (u, f(u)) and (v, f(v)) are, respectively, low and high points for a continuous function, /, on an interval, [p, q], then f(u)(q — p) < f£ f(x) dx < f(v)(q — p).

We now examine what happens to the three terms in the inequality string

(x) (xi) (xii)

/(*) < G( X + h l~ G ^ X) <f(x + h)

as h gets close to zero.

(x) Because f(x) is not affected by h, f(x) remains fixed as h gets close to zero.

Explore 10.2.2 Do This. Give reasons for (xi) and (xii).

i • \ ,. G(x + h)-G(x)

xi hm ; = G + (x)

h^o+ h

(xii) ^lini f(x + h) = f(x)

We conclude that

(x) (xi) (xii)

f(x) < °( X + G ^ < f(x + h) As/wO I | |

f(x) < G’ + (x) < f(x)

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

460

It follows from f(x) < G’ + (x) < f(x) that G’ + (x) = f(x) for a < x < b. A slight modification of this argument shows that G’~(x) = f(x) for a < x < b. and we conclude that G'(x) = f(x) for a < x < b. Because G'(a) = G’ + (a) and G'(b) = G’-(b), G'(x) = f(x) for a < x < b.

Slightly modified arguments yield the same conclusion for / a decreasing function. End of proof.

Example 10.2.1 Although technical in statement, the Fundamental Theorem of Calculus agrees with your intuition.

1. If v(t) is the velocity of a particle at time t, then G(x) = Jq v(t) dt is the displacement of the particle during the time interval [0,x]. The Fundamental Theorem of Calculus states that G'(x), the rate of change of displacement, is v(x), the velocity.

2. If r(t) is the rate at which urea is produced in a patient without functional kidneys, then G(x) = Jq r(t) dt is the total amount of urea in the body x hours since the last dialysis. The Fundamental Theorem of Calculus states that G'(x), the rate of change of total urea, is r(x), the rate at which it is produced.

3. If b(t) and d(t) are the birth and death rates of a population at time t, then r(t) = b(t) — d(t) is the growth rate (which may be negative). G(x) = Jq r(t) dt is the population increase (again, it could be decrease) during the time interval [0, x\. The Fundamental Theorem of Calculus states that G'(x), the rate of change of population, is r(x), the growth rate.

4. In Example Figure 10.2.1.1, for 1 < x < 4, let A(x) be the area of the region bounded by the graph of /, the t-axis, and the lines t = 1 and t = x. The rate at which the area, A, increases at x, A'(x), is fix) the height of the graph at x.

Figure for Example 10.2.1.1 A(x) is the area between the graph of /, the t-axis, t = 1 and t = x. A'(x), the rate at which the area A increases at x, is f(x).

A'(x) = f(x)

y = f(t)

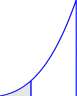
0

0

a

x

b

Exercises for Section 10.2, The Fundamental Theorem of Calculus. Exercise 10.2.1 Work Explores 10.2.1 and 10.2.2

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

461

Exercise 10.2.2 a. Draw an approximation to the graph of the function G defined in Example Figure 10.2.1.1. Suggestion: Partition the interval [1,4] into six equal subintervals, [1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0] and estimate /(1.0), /(1.5), • • •, /(4.0). Then estimate G(1.0), (2(1.5), • • •, (3(4.0) using trapezoidal approximations.

b. Estimate (?'(1.5) using each of the three difference quotients:

Backward Centered Forward

(3(1.5) -(3(1) 1.5- 1

G(2)-G(l) 2 – 1

G(2) – (3(1.5) 2 – 1.5

The best estimate would normally be the centered difference quotient. Compare this estimate with your estimate of /(1.5).

c. Use your data to estimate (3′(3.5) and compare your estimate of (3′(3.5) with /(3.5). Exercise 10.2.3 Let

f(t)

1

-t 2 /2

and

G(x)

‘2-k Jo G(x) is the area of the region bounded by the graphs of

1

f(t)dt

1

‘ t2 ‘ 2 dt

0 V27T

y = f(t)

-t 2 /2

2,71

y = 0

t = 0

and

t = x

in Exercise Figure 10.2.3. Included in the figure are some data for both / and G.

Figure for Exercise 10.2.3 Graph of fit)

1

-t 2 /2.

271

G(x) is the area of the shaded region

between the graph of /, y — 0, t — 0 and t = x.

0.2 t = 0

a. Write the formula for /(0.6) and evaluate it.

b. Use the values of f(0) /(0.2), /(0.4) and /(0.6) and the trapezoidal approximation to estimate G(0.6).

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

462

c. Approximate G'(l.O) from the data for G. using the backward, centered, and forward difference quotients and compare these estimates with /(1.0).

Exercise 10.2.4 Let G(x) be the area of the region bounded by the graphs of y — y — 0, t — 1 and t = x.

a. Compute approximate values for y(1.0), y(1.5), y(2.0), y(2.5), and y(3.0).

b. Compute approximate values for (2(1.0), G(1.5), G(2.0), G(2.5), and G(3.0).

c. Sketch the graph of y — on [0,3].

d. Sketch the graph of G on [1,3].

e. Estimate G'{2).

Exercise 10.2.5 At 1:00 a.m. an oil pipe line bursts and starts releasing oil into a lake at the rate of 2 cubic meters per hour. At 2:00 a.m., a second oil pipe line bursts and also starts releasing oil into the lake at the rate of 3 cubic meters per hour.

a. How much oil is in the lake at 1:00, 1:30, 2:00, 2:30, 3:00, 3:30, and 4:00?

b. Let T(x) be the total amount of oil in the lake at time x. Draw a graph of T.

c. Write equations describing the total amount of oil, T(x), in the lake for each time x between 1:00 a.m. and 4:00 a.m.

d. Compute V.

Exercise 10.2.6 This problem illustrates the necessity of the hypothesis that / be continuous in the statement of the Fundamental Theorem of Calculus. Remember that the integral is defined for any nondecreasing function. Let

For each x in [1,4], let G(x) be the area of the region between the graph of / and the horizontal axis and between t — 1 and t = x. See Exercise Figure 10.2.6

a. Compute G(1.0), G(1.5), G(2.0), G(2.5), G(3.0), G(3.5) and G(4.0).

b. Draw a graph of G.

c. Write equations describing G.

d. Write G(x) as an integral.

e. Compute and draw the graph of G’.

fit)

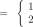
For For

1 < t < 2

2 < t < 4

f. G’ and / are not the same function. What is the difference?

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

463

Figure for Exercise 10.2.6 Graph of / where f(t) = 1 for 1 < t < 2 and f(t) = 2 for 2 < t < 4 and the region G bounded by the graph of f, y = 0, t = 1 and t = x.

0 I 1 1 L

0 1 2 „ 3

Exercise 10.2.7 Let F(t) = [t] where [t] is the greatest integer less than or equal to t. For example, [n] = 3, and [2] = 2. Let G(x) = / 0 e f(t) dt for 0 < x < 4.

a. Sketch the graph of / for 0 < t < 5

b. Sketch the graph of G.

c. Sketch the graph of G’.

d. You should find that G’ ^ f. Does this contradict the Fundamental Theorem of Calculus?

Exercise 10.2.8 Use your calculator to solve the previous problem (slowly). In GRAPH, use MORE to find FORMT. Under FORMT select DrawDOT. In GRAPH go to y(x) =. Write ‘yl = int x’. You can find ‘int’ in 2nd MATH NUM. Write ‘y2 = fnlnt(yl,x,0,x)’. You can find fnlnt in 2nd CALC. Set you window to 0 < x < 4, 0 < y < 6. Press DRAW. Your calculator will draw the graph of / and the graph of G. Plan to work some other problems while you wait. It takes about 12 minutes to compute.

Exercise 10.2.9 The the following two MATLAB ‘m’ files solve Exercise 10.2.7.

File 1 myfun_floor.m

function y=myfun_floor(x) y=floor(x);

File 2 test_int.m

close all;clc;clear

z=[0:0.01:4]; u=floor(z);

for k=l:length(z)

v(k)=quadgk(@myfun_floor,0,z(k),’waypoints’,[1,2,3]);

end

plot(z,u,’.’); hold(‘on’); plot(z,v,’r.’)

myfun_floor.m and test_int.m should be in the same directory. Issue the MATLAB command, test_int In MATLAB, floor (z) rounds the elements of z to the nearest integers towards minus infinity.

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

464

10.3 The parallel graph theorem.

The Parallel Graph Theorem is needed in order to make full use of the Fundamental Theorem of Calculus. A preliminary version is the Horizontal Graph Theorem.

Theorem 10.3.1 Horizontal Graph Theorem. If D is a continuous function defined on an interval [a, b] and for every number x in (a, b),

D'(x) = 0,

then there is a number C such that for every number x in [a, b]

D{x) = C.

Proof. Let C = D(a). Suppose x is in (a,b). By the Mean Value Theorem 12.1.1 there is a number z between a and x such that

D(x) – D(a) = D'(z) (x – a).

Because D'(z) = 0, D(x) — D(a) = 0 and D(x) = D(a) = C. Because D is continuous and D(x) = C for every x in [a, b), D(b) = C. End of proof.

An example of parallel graphs, that is, graphs which have the same derivative, is shown in Figure 10.4.

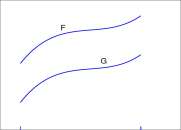
a b

Figure 10.4: The graphs of F and G have the same derivative and are parallel.

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

465

Theorem 10.3.2 Parallel Graph Theorem. If F and G are functions defined on an interval [a, b] and for every x in [a, b]

F'(x) = G'(x),

then there is a number, C, such that for every x in [a, b]

F(x) = G(x) + C

Proof. Let D(x) = F(x) — G{x) for every x in [a, b}. Then

D\x) = [F{x) – G(x)]’ = F'(x) – G'{x) = 0

for every x in [a, b). By the Horizontal Graph Theorem, Theorem 10.3.1, there is a number C such that for every x in [a, b], D(x) = C. Then for every x in [a, b]

D(x) = F(x) – G(x) = C and F(x) = G(x) + C.

End of proof.

The power of the Fundamental Theorem of Calculus augmented by the Parallel Graph Theorem is illustrated by the next example.

Example 10.3.1 A lOcc syringe has cross-sectional area A cm 2 ; air inside the plunger is atmospheric pressure P 0 which we assume to be 1 Atmosphere (1 Atm); the plunger is a the 10 cc mark and the neck of the syringe is blocked. The plunger is depressed a distance s/A to the 10 — s cc mark. Because at constant temperature, PV = a constant = Pq Vq, = Po,the pressure, P s , inside the syringe is Pq 10/(10 — s). The force on the plunger is (P s — Po) A = A P 0 (s/ (10 — s). The work done in compressing the air from 10 cc to 5 cc is

/ AP 0 – d-= / Pojj—ds

Jo 10 — s A Jo 10 — s

Let

W(x) = Po f ds Jo 10 — s

Then the work done in compressing the air is W(5). The Fundamental Theorem of Calculus asserts that

Let uj(x) be defined by (a bolt out of the blue!)

u(x) = Po [-10 ln(10 -x)-x] Explore 10.3.1 Use derivative formulas including f(t) = \nU(t) =^ f'(t) = ]j^U'(t) to show that

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

466

Thus W'(x) = uj'(x) for every x in [0, 5], and by the Parallel Graph Theorem there is a number C such that such that for every number a; in [0, 5]

W(x) = lo(x) + C

Now

W(0) = P 0 / — ds = 0, and

io 10 — s

w(p) = P 0 [-10 ln(10 – 0) – 0] = -P 0 10 In 10. Because W(0) = u(0) + C

0 = -P 0 10 In 10 + C and C = P 0 10 In 10.

We can conclude that for all x in [0, 5]

W(x) = P 0 [-10 ln(10 -x)-x]+P 0 10 ln(10)

The total work done in compressing the air as

W(5) = P 0 [-10 ln(10 – 5) – 5 + 10 ln(10)] = P 0 1.93

In the previous example, we used the Fundamental Theorem of Calculus to evaluate the integral without computing an approximating sum. It was important to have a function, to, satisfying u’ = W, and in a sense, the problem of computing approximating sums was exchanged for the problem of finding u. Once we found such an uj, we appealed to the Parallel Graph Theorem to conclude that there was a number C such that for all x, W(x) = u(x) + C. This is powerful medicine!

Exercises for Section 10.3 The parallel graph theorem.

Exercise 10.3.1 Let f(x) = [x] (= greatest integer less than or equal to x) 0 < x < 5. Compute and draw the graph of /’. Is this a example showing that the Horizontal Graph Theorem, Theorem 10.3.1, is false?

Exercise 10.3.2 Suppose P(t) is the size of a population at time t, P(0) = 5000, and P'(t) = 0 for all t. What is P(100)? What is P(10000000000)?

Exercise 10.3.3 Suppose a mold colony is growing in a nutrient solution and that on day zero the area was 0.5 cm 2 and for every time, t > 0, the instantaneous rate of growth of the area of the colony is 2t cm 2 per day. Let P(t) be the colony area at time t.

a. Argue that for every time, t, P'(t) = It.

b. Show that for Q{t) = t 2 , Q'(t) = 2t. Then P'{t) = Q'(t).

c. From the Parallel Graph Theorem, it follows that there is a constant C such that P(t) = Q(t) + C.

d. Use P(0) = 0.5 to evaluate C.

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

467

e. What is the area of the mold colony on day 8?

Exercise 10.3.4 Suppose the rate of glucose production in a corn plant is proportional to sunlight intensity and can be approximated by

R(t) — K (t + 7) 2 (* – 7) 2 = K (t 4 – 98t 2 + 240l) – 7 < t < 7

Time is measured so that sunrise is at -7 hours, the sun is at its zenith at 0 hours and sets at 7 hours. The quantity Q(x) of glucose produced during the period [—7, x] is

/X PX PX

R(t) dt = J K (t 4 — 98t 2 + 240l) dt = K J (t 4 – 98t 2 + 240l) dt

By the Fundamental Theorem of Calculus,

Q'(x) — K (x 4 – 98x 2 + 240l)

a. Sketch the graph of R(t). At what time is the sun most intense?

b. Show that if U(x) — y then U'(x) = x 4 .

c. Find an example of a function, V(x) such that V'(x) = —98x 2 .

d. Find an example of a function, W(x) such that W'(x) = 2401.

e. Let G(x) — K (f – f x 3 + 2401a;). Show that G'(x) = Q'(x).

f. Conclude that there is a number, C, such that

“x 5 98

Q(x) = G(x) + C = K

– —x 3 + 2401a; 5 3

+ C

g. Why is Q(-7) = 0.

h. Evaluate C.

i. Compute Q(7), the amount of glucose produced during the day.

Exercise 10.3.5 “Based on studies using isolated animal pancreas preparations

maintained in vitro, it has been determined that insulin is secreted in a biphasic manner in response to a marked increase in blood glucose. There is an initial burst of insulin secretion that may last 5-15 minutes, a result of secretion of preformed insulin secretory granules. This is followed by more gradual and sustained insulin secretion that results largely from biosynthesis of new insulin molecules. ” (Rhoades and Tanner, P 710)

a. A student eats a candy bar at 10:20 am. Draw a graph representative of the rate of insulin secretion between 10:00 and 11:00 am.

b. Draw a graph representative of the amount of serum insulin between 10:00 and 11:00. Assume that insulin is degraded throughout 10 to 11 am at a rate equal to insulin production before the candy is eaten, and that serum insulin at 10:00 was Iq.

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

468

c. Write an expression for the amount of serum insulin, I(t), for t between 10:00 and 11:00 am.

Exercise 10.3.6 Equal quantities of gaseous hydrogen and iodine are mixed resulting in the reaction

which runs until I 2 is exhausted [H 2 is also exhausted). The rate at which I 2 disappears is ^°’^ 2 gm/sec. How much I 2 was initially introduced into the mixture?

a. Sketch the graph of the reaction rate, r(t) = jp^yi-

b. Approximately how much I 2 combined with H 2 during the first second?

c. Approximately how much I 2 combined with H 2 during the second second?

d. Let Q(x) be the amount of I 2 that combines with H 2 during time 0 to 2; seconds. Write an integral that is Q(x).

e. What is Q\x)l

f. Compute W'{x) for W(x) = =^.

g. Show that there is a number, C, for which Q(x) = W(x) + C.

h. Show that C = 0.2 so that Q(x) = 0.2 – g.

i. How much I 2 combined with H 2 during the first second?

j. How much I 2 combined with H 2 during the first 100 seconds? k. How much I 2 combined with H 2 1

10.4 The Second Form of the Fundamental Theorem of Calculus

The Parallel Graph Theorem leads to a second form of the Fundamental Theorem of Calculus that has powerful applications.

H 2 + I 2

2HI

Theorem 10.4.1 Fundamental Theorem of Calculus II. Suppose / is a continuous function defined on an interval [a, b] and F is a function defined on [a, b] having the property that

for every number t in [a, b] F'(t) = f(t)

(10.5)

Then

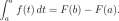
•6

(10.6)

Proof: Suppose the hypothesis of the theorem. Let G be the function defined on [a, b] by

G(x)= f f(t)dt

J a

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

469

Explore 10.4.1 Do this. Give reasons for the steps (i), ■ ■ ■ , (v).

For x in [a,b], G'(x) = f(x). (i) For x in [a, b], F'(x) = fix). (ii) For x in [a,b], G'(x) = F'(x).

There is a number C so that for x in [a, 6], G(:r) = F(x) + C (iii) G{a) = 0. (iv) G(a) = F(a) + C. Therefore, C = -F(a). G(x) = F(x)-F(a). G(b) = F(b) – F(a).

f a f{t) dt = F(b) – F(a) . (v) End of proof.

Notation: The number F(b) – F(a) is denoted by [ F(x) } b a or F(x) \ b a .

Example 10.4.1 You now have a powerful computational tool. 1. Evaluate Jq t 2 dt. Check that

t 3

if F(t) = – then F'(t)

It follows that

f 1 t 2 dt = F(l) – F(0) Jo

l [t3]/ = l 3t2 = t2 –

~3 ~ ~3 ~ 3′

The integral is the area of the region bounded by the graphs of y = t 2 , y = 0, and t — 1. The area was also found to be | in Chapter 9 by use of rectangles and approximations.

2. Evaluate f 2 t 2 dt. Using the same function, F(t) = y we obtain that

j\ 2 dt = F(2)-F(l)

3. Evaluate J 0 5 5e omt dt. Observe that F(t) = 250 e omt has the property that F'(t) = 5e

o 0.02t

Therefore

5 e omt dt = F(5) – F(0) = [250 e a02 *1 5 = 250 e a02 5 – 250 e 0 ‘ 02 0 = 26.29

J0 L Jo

4. Evaluate J 2 \ dt. We found in Chapter 5 that F(t) = hit =>- F'(t) = \. Therefore,

f 2 -dt = F(2)-F(l) = [hit] 2 = ln2-lnl = In2 J i i

Exercises for Section 10.4, The Second Form of the Fundamental Theorem of Calculus. Exercise 10.4.1 Do Explore exercise 10.4.1. Exercise 10.4.2 Evaluate the integrals

Exercise 10.4.3 Evaluate the integrals.

a. ji 3 * 2 (ft b. J 0 2 t 3 dt c. / 0 2 e*df d. J 3 \ dt e. J* (1 + 1) 2 dt

f. J 3 5tdt g. J 2 t + 5dt h. jo 2 e 2t dt i. /„ 3 e-*dt j. J 3 (l + t 2 )cft

Exercise 10.4.4 The graph in Figure 10.4.4 approximates the size, S'(i), of colon carcinoma cells t days after injection into mice (after Leach, D. R., et al, Science 271 (1996) 1734.)

a. Read approximate values of S(t) and S'(t) from the curve.

b. From the (completed) table of values of S'(t) approximate J 3 5 5 S'(t) dt.

c. Give a physical interpretation of J 3 5 5 S'(t) dt.

d. Why would you expect J 3 5 5 S'(t) dt to be approximately 130 according to data in the table?

Figure for Exercise 10.4.4 The size of carcinoma cells t days after injection into mice. Error

bars that were on the original graph are omitted.

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

471

E

5 10 15 20 25 30 35 40

Days

Exercise 10.4.5 a. Let y = arctan x so that x = tan y(x). Show that

sec 2 y(x) = 1 + x 2 .

b. Use x = tan y{x) and the chain rule, [G{u{x))] = G'(u(x)) u'(x), to conclude that

1 = (sec 2 y(xf) y\x) and y'(x) = —— 5 .

c. Use the result of b. to show that i ^

/ o doc —

io l + r 4

10.5 Integral Formulas.

Because the problem, “Find F(t) such that F'(t) = /(£)” occurs with each application of the Fundamental Theorem of Calculus II, extensive tabulations of solutions to the problem (called antiderivatives or indefinite integrals) have been made during the 300 years since calculus was first introduced. I. S. Gradsteyn and I. W. Ryzhik list some 2000 – 2500 antiderivatives in their “Table of Integrals Series and Products”, Academic Press, 1965. More recently, computer programs have been written that provide a rich supply of antiderivatives (Mathematica, Derive, Maple, MATLAB) and some hand held calculators will solve most of the commonly encountered problems. The antiderivatives are denoted by

‘ /(*) dt

and are called indefinite integrals because the interval of integration is not specified (there are no lower and upper limits of integration). Because the derivative of a constant function is zero, every indefinite integral is really a set of functions, each two members of which differ by a constant. The common notation always includes an additive constant in the solution. For example,

x dx — ~\~ C 3

(10.7)

is read, ‘the indefinite integral of x 2 is y + C” where it is understood that C is a constant. The implication is that every function whose derivative is x 2 is of the form, y + C.

For every derivative formula, there is an indefinite integral (antiderivative) formula. There follows a table of indefinite integral formulas corresponding to the derivative formulas on page 390.

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

472

J Odt ldt

t n dt

= C

t + C

(10.8) (10.9)

/

m+l

n +

– + C forra^-1 (10.10)

J KP(t)dt J [fit) + g[t)] dt [f{t) g(t) + f(t) g'{t)]dt J G'[u{t)\ u'(t)dt

[u(t)] n u'(t) dt J e u{t) u'(t) dt

J e l dt J sin t dt

I

cos tdt =

e l + C (10.11)

\nt + C (10.12)

-cos t + C (10.13)

sin t + C (10.14)

K J P(t)dt

J f(t)dt + J g(t)dt

fit) g(t) + C

G[u(t)\ + C u(t) n+1

I 4t«'(*)

J u(t) v ;

dt

J sin-u(t) u'(t) dt J cos u(t) u'(t) dt J e kt dt

n + 1

= e u(t) + C

= \n[u(t)]+C

= cosw(t) + C = — sin-u(t) + C

= \e kt + C k

+ C for n ^ 0

(10.15) (10.16) (10.17) (10.18)

(10.19) (10.20) (10.21)

(10.22) (10.23) (10.24)

An easy aspect of antiderivative formulas is that they can be checked readily by differentiation. For example, Equation 10.10 asserts that all functions whose derivative is t n are of the form

+ C. We can check that all such functions have t n as their derivative:

d ~dt

t n+1 n + 1

C

d ~dt

/■n+1

n + 1

= m( n+1 ) r+0

= t n .

Equation 3.30

Equation 3.29 Equation 3.27 Equation 3.29

That there are no other such functions is a consequence of the Parallel Graph Theorem.

The indefinite integral formulas enable computation of antiderivatives of all polynomials; in

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

473

fact, only four of the antiderivative formulas are needed. For example

/ [5t 7 – 3t 4 + 2] dt = J [5t 7 ] dt-J [3t 4 ] dt + J2dt Equation 10.16

= 5Jt 7 dt-3Jt 4 dt + 2Jldt Equation 10.15

= 5 = 5

= ft 8 – ft 5 + 2t + C.

The constant terms included in the antiderivatives are usually suppressed until the last step, and are treated as rather pliable objects. For example, C in the last equation above is 5Ci — 3C*2 + 2C3. Because a linear combination of constants is just a constant, and because subscripts are a nuisance, one often sees algebraic steps that would imply

5C – 3C + 2C = C.

Students usually adapt to this murky algebra without suffering serious damage, but it seems only fair to warn you of this practice, as we will will follow it subsequently.

10.5.1 Using the chain rules.

Equations 10.18 through 10.23 are all consequences of a chain rule for derivatives and always when using one of these equations it is important to identify u(t), G'(u), u'(t) and G{u).

Example 10.5.1 Two antiderivative problems that appear similar,

J e (t2) dt and J e {t2) tdt

are peculiarly different. The first has no expression in familiar terms. The second is easy. In the second equation, identify

Then

u(t) = t 2 , / e^tdt

G\u) = e u , u\t) = 2t and G(u) = e v

■■ J \ e^2tdt : \ J e(* 2 ) (2 t) dt ■■ \ J e”W u'{t) dt

Arithmetic Equation 10.15

\e u ^ + C \ e(‘ 2 ) + C

Equation 10.20

Example 10.5.2 Consider solving the two problems

J (l + * 4 ) 10 t 3 dt or

/(l + f)

10

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

474

Because (1 + t 4 ) 10 can be expanded by multiplication (using either the binomial expansion formula or by making nine multiplications) and the expanded form is a polynomial, both integrands of these two problems are polynomials and the antiderivatives of polynomials can be easily computed. The first integral can be solved without expansion, however, and is easier to compute. Identify

u 11

u(t) = 1+t 4 , G\u) = u 10 , u’ {t) = At 3 and G{u) = ] Then

J (1 + t 4 ) 10 1 3 dt = J I (1 + t 4 ) 10 4t 3 dt Arithmetic

= I J (1 + t 4 ) 10 (4t 3 )dt Equation 10.15

= \l ( u (t)) W u'(t)dt Substitution

= | ^ffl n + C Equation 10.19

= | V n J +C u(t) = l + t 4

Students sometimes attempt to solve / (1 +1 4 ) 10 1 2 dt by the following means. They are thinking of

v 11

u(t) = 1+t 4 , G'(u) = u 10 , u'(t) = At 3 and G{u) = — J (1 + t 4 ) 10 1 2 dt = J ^ (1 + t 4 ) 10 At 3 dt Algebra

= 4^/ (1 + ^ 4 ) 10 4t 3 rft UGH!

The last step is incorrect because ^ is not a constant. The corresponding step in the previous

argument is correct because | is a constant and Equation 10.15 asserts that

/ K f(t) dt — K J f(t) dt when K is a constant. It is incorrect when K is not constant. ■

Example 10.5.3 Compute / sin(7rt) dt. Identify

u(t) = nt, G'{u) = sin-u, u'(t) = n and G(u) = —cosu

Then

J sin( Tit) dt = J — sin( nt ) n dt = —J sin( irt) ir dt =

1 r 1 1

– / sin( u(t) ) u'(t) dt = -( – cos( u(t)) ) + C = ( cos(Trt) ) + C m

7T J IX IX

Example 10.5.4 Compute / y/ht – Adt. Identify

u(t) = 5t-A, G'{u) = (u) 1/2 , «'(*)= 5 and G(u)

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

475

Then

j V^t^Adt = V5t^A5dt = ^J(u{t)f/ 2 u'{t)dt = 1 ( ^ 2 )3/2 +C

15 V ;

Example 10.5.5 Compute / (lnt) 3 \dt. Identify

1 u 4 u{t) = lnt, G'{u) = u 3 , u'(t) = – and G(u) = —

t 4

Then

J {\ntfjdt = J (u(t)) 3 u'(t)dt = { -^p^ + C = { -^p^ + C m Example 10.5.6 Compute / tanxdx. This is a good one. First write

J tan x dx = J

Then identify

SIM

dx

cosx

u(x) = cosx, G'(u) = —, u'(x) = — sinx and G(u) = Inu

u

Then

dx

f f S1I1X 1 f 1 / • N , f 1 // X

/ tana; = / dx = — (— smx)dx = — u (x)

J J cosx J cosx J u(x)

= — In u(x) + C = — lncosx + C = lnsecx + C ■

Always, once an antiderivative has been computed, it can be checked by differentiation.

We check the last claim that / tan x = In sec x + C by differentiation. We should show that [In sec a;]’ = tana:.

[In sec x V = [sec a;]’ = sec x tan x = tanx

sec x sec x

10.5.2 Integration by parts.

Equation 10.17

r [f'(t)g(t) + f(t)g'(t)]dt = fit) g{t)+ C

may be rewritten as

J f{t) g’it) dt = fit) git) – J fit) git) dt (10.25)

Equation 10.25 exchanges the problem, / f(t) g’it) dt for the problem / f'(t) git) dt. There are times when that is a good trade, but some cleverness is required to recognize when a good trade is

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

476

possible. The process is called integration by parts, f(t) and g'(t) being the parts in the first integral and f'{t) and g(t) being the parts in the second integral. In computing / t sintdt, there is a good trade. Identify

fit) = t and g'(t) = sint fit) = 1 g{t) = -cost

Then

J t sintdt = t (— cost)— / 1 (— cost) dt

= —t cost + sint + C In computing / t 2 sintdt, two good trades can be made. First we identify

f[t) = t 2 and g'(t) = sint fit) = It git) = -cost

Then

Next we identify

f t 2 sintdt = t 2 (-cost) -/ 2t (-cos t) dt fit) = It and g'(t) = -cost

and write

/ t 2 sintdt

A chart to keep track of these computations is shown in Figure 10.5. You may see from the chart or an expansion of it how to compute / t 2 costdt and / t 3 sintdt and / t 3 e t dt.

Exercises for Section 10.5, Integral Formulas.

Exercise 10.5.1 Use your technology to find a fourth degree polynomial close to the data in the table below taken from the graph of average solar intensity at Eugene, Oregon in Figure 9.1.3 on page 405.

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

477

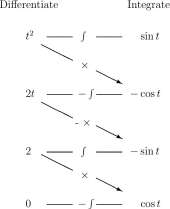
Figure 10.5: Chart for computing the terms for integration by parts.

Your technology will object that the equations to compute the coefficients of a fourth degree polynomial to the Day – Solar Intensity data are ill conditioned (subject to roundoff error); the equations to fit Day minus 180 – Solar Intensity are OK. Therefore, fit a fourth degree polynomial to the Day minus 180 – Solar Intensity data, and interpret the polynomial according for plotting the data and for integration. You should get

P(t) = 8.7339 10~ 9 (t- 180) 4 – 1.2225 10~ 7 (t – 180) 3 -4.5587 10~ 4 (t – 180) 2 +3.4149 10~ 3 (t – 180) + 6.63072

a. Plot the data and a graph of your polynomial.

b. Compute the integral of J 0 365 P2(t)dt.

c. Compare your answers to the estimate of 1324 computed using the trapezoid rule on 12 intervals of length 30 and one interval of length 5, in Exercise 9.1.3 on page 404.

Exercise 10.5.2 Check by differentiation the validity of the indefinite integral formulas:

a. J * dt = lnt + C b. J [U(t)] n U'(t) dt = ^j”^ + C c. J e kt dt = *e kt + C

Exercise 10.5.3 Compute j* (1 + t 4 ) 3 dt.

Exercise 10.5.4 Which of the two indefinite integrals

f : – dt or f – – – dt J 1 + 1 2 J 1 + t 2

CHAPTER 10. THE FUNDAMENTAL THEOREM OF CALCULUS

478

Exercise 10.5.5 Compute the following integrals and antiderivatives. For the definite integrals, draw a region in the plane whose area is computed by the integral. If you solve the integral by a substitution, u(t) =, then identify in writing u(t) and u'(t).

(b) Compute J{ \nxdx

c. (a) Show that | + ^ = t ^_ t ^ (b) Compute / ^fr^y dt

Compute sin 2 9 d6 d. (a) Believe: [arcsinrr]’

(b) Compute J 0

1/2 1

dx

X/

Exercise 10.5.9 Solve using integration by parts, / u(x) v'(x) dx = u(x) v(x) — J v(x) u\x) dx (or / udv = uv — J v du).

a. J xe x dx b. J xliaxdx c. / xsmxdx d. J x 2 e x dx

e. / xe 2x dx f. jlnx-ldx g. J xcosxdx h. / x 3 e x dx

Exercise 10.5.10 a. Use integration by parts on / e x sinxdx, with u(x) = e x and v'(x) = sinx, to show that

J e x sinx dx = — e x cosx + J e x cosxdx. Use a second step integration by parts on / e x cos x dx to show that

J e x cos x dx = e x sin x — J e x sin x dx Combine the previous two equations to show that

J e x sin x dx = ^e x (sinx — cosx) + C

b. Do two steps of integration by parts on

J e x cosxdx and show that J e x cosx dx = -e x (sinx + cosx) + C

c. Do two steps of integration by parts on

J (sinx)e~ x dx and show that J e^ 11 sinxdx =-(e _7r + 1)

d. Clever! Note that / dx = J 2^c ^ dx.

Let u = 2^/x and v’ = — -= and show that

2y/x

J e ^dx = 2^ce^ – 2e^ + C

Chapter 11

Applications of the Fundamental Theorem of Calculus and Multiple Integrals.

Where are we going?

Several of the traditional applications of the Fundamental Theorem of Calculus and a definition of integrals of functions of two variables are included in this chapter.

The Fundamental Theorem of Calculus II, symbolically written

f F'(t)dt = F(b)-F(a) = [F(t)] b a = F(t)\ b a , (11.1)

J a

replaces tedious computations of the limit of sums of rectangular areas with an often easier problem of finding an antiderivative. The theorem is widely applied in physics and chemistry and engineering. It is useful in biology, but less widely so because the integrands, f(t), often are not expressed as elementary functions. Indeed, the integrands in biology may be only partly specified as tables of data, in which case the options are to (1) compute a rectangular or trapezoidal sum or (2) approximate the data with an elementary function (a polynomial, for example) and compute the integral of the elementary function using Equation 11.1.

11.1 Volume.

Example 11.1.1 How to find the volume of a potato.

A potato is pictured in Figure 11.1 A with marks along an axis at 2 cm intervals. A cross section of the potato at position 10 cm showing an area of approximately 17 cm 2 is pictured in Figure 11.IB. The volume of the slice between stations 8 cm and 10 cm is approximately 2 cm x 17 cm 2 = 34 cm 3 . There are 9 slices, and the volume of the potato is approximately

9

( Area of slice k in cm 2 ) x 2 cm.

k=l

The approximation works remarkably well. Several students have computed approximate volumes and subsequently tested the volumes with liquid displacement in a beaker and found close agreement.

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

481

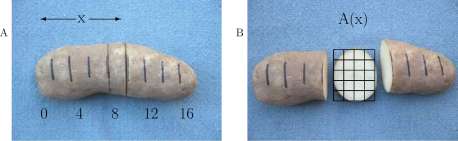
Figure 11.1: A. A potato with 2 cm marks along an axis. B. A slice of the potato at position x = 10 that has approximately 17 cm .

The sum is also an approximation to the integral

17

A(x) dx,

where A{x) is the area of the cross section of the potato at station x, and the integral may be considered to be the actual volume. ■

The principle applies to any three dimensional region, R. Assume there is an axis L and for each station x between stations a and b along the axis, the area A(x) of the cross section of R perpendicular to L at x is known. If A = [xq, X2, x% • • ■ x n -i, x n] is a partition of [a, b]. Then

Volume of R

A(x k ) (x k – x k -i)

k=l rb

—► / A(x)dx as |A| —> 0.

J a

Using this procedure, volumes of a large number of regions can be computed.

11.2)

Example 11.1.2 The volume of a sphere. Consider a sphere with radius R and center at the origin of three dimensional space. We will compute the volume of the hemisphere between x = 0 and x = R. See Figure 11.2A. Suppose x is between 0 and R. The cross section of the region at x is a circle of radius r and area nr 2 . Therefore

2 1 2 r + x

R 1

R 2 -x 2

and

A

A{x) = tt(R 2 -x 2 ).

Consequently the volume of the hemisphere is

V = f R n(R 2 – x 2 ) dx Jo

The indefinite integral is the antiderivative of a polynomial, and

‘(R 2 — x 2 ) dx = (ttR 2 — ttx 2 ) dx = irR 2 x — ir

7T

X

+ C.

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

482

A

B

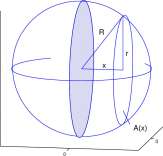
A(z k )

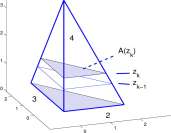
Figure 11.2: A. A sphere of radius R. The cross section a distance x from the center of the sphere is a circle of radius r = \/R 2 — x 2 . B. A triangular solid; the edges of lengths 2, 3, and 4 are mutually perpendicular.

By the Fundamental Theorem of Calculus II,

V — [ R rr(R 2 – x 2 ) dx Jo

nR x — TV

x”

R

ttR 2 x R – it—\ – (tvR 2 X 0

7T-

The volume of the sphere is twice the volume of the hemisphere.

ttR

1 o

The volume of a sphere of radius R is -irR

3

This formula was known to Archimedes and perhaps to mathematicians who preceded him, and is easily computed using Equation 11.2. Archimedes and his work are fascinating; a short description of them can be found at www.uz.ac.zw/science/maths/zimaths/33/archimed.htm. and a longer description is in http://en.wikipedia.org/wiki/Archimedes. ■

Example 11.1.3 Compute the volume of the triangular solid with three mutually perpendicular edges of length 2, 3, and 4, illustrated in Figure 11.2B.

At height z, the cross section is a right triangle with sides x and y and the area A(z) =

1

x x y. Now

Therefore

x 4 — z 2 3

– = —|— so x = -(4-z). Similarly, y=-(A-z).

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

483

A

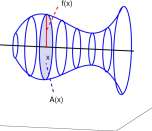
B

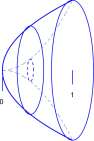
Figure 11.3: A. A solid of revolution. A cross section at station x is a circle with radius f(x) and lias area A(x) = n ( f(x) f. B. Solid generated by rotating the region between y = x 2 (dashed curve) and y = \fx about the x-axis.

and

Check that

V= / A(z)dz Jo

4 3

o 16 (4 – zf. Then

(4 – zf dz

3 r 4

16 Jo

(4 – zfdz.

— (\A-z) 2 dz=-16 Jo v ; 16

(4 – zf

16

(-o

(4) ;

))=4.

Example 11.1.4 Volume of a solid of revolution. Equation 11.2 is particularly simple for solids of revolution. A solid of revolution for non-negative function / is shown in Figure 11.3A. The cross section at station a; is a circle of radius f(x) and has area A(x) = n ( f(x) f. From Equation 11.2 the volume is

Volume of a solid of revolution

A(x) dx

n(f(x)fdx

11.3)

Problem. Find the volume of the solid S generated by rotating the region R between y = x 2 and y = y/x about the rc-axis. See Figure 11.3B.

Solution. There are two problems here. First we compute the volume of the solid, Si, generated by rotating the region below y = ^Jx, 0 < x < 1, about the x-axis. Then we subtract the volume of the solid, S2, generated by rotating y = x 2 ,0<x<l about the x-axis.

Volume of Si Jq 1 tv {\fxf dx = n Jq xdx = w

x 2 2

7T 7

Volume of S 2 Volume of S

Jq 1 7t (x 2 ) 2 dx = iv Jq 1 x 4 dx

x 5 IT

71

5

7T 1

71

5

3tt 10

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM Alternatively, we can compute the area of the ‘washer’ at x which is

484

A(x) = TT — TT (x 2 ^ = 7T (x — X^

Then

Volume of S

j tt (x — x 4 ^j dx

TT

Exercises for Section 11.1, Volume

Exercise 11.1.1 Data for all of the slices of the potato shown in Figure 11.1 are:

Slice Position (cm) 2 4 6 8 10 12 14 16 Slice Area (cm 2 ) 11 15 14 16 17 15 13 10

Approximate the volume of the potato.

Exercise 11.1.2 The Visible Human Project at the National Institutes of Health has provided numerous images of cross sections of the human body. They are being integrated into the medical education and research community through a program based at the University of Michigan. Shown in Exercise Figure 11.1.2 are eight cross sections of the right side of the female brain. Your job is to estimate the volume of the brain. Assume that the sections are at 1 cm separation, that the first section only shows brain membrane, and that the scale of the cross sections is 1:4. Include only the brain and not the membrane which is apparent as white tissue. We found it useful to make a 5mm grid on clear plastic (the cover of a CD box), each square of which would be equivalent to 4 cm 2 . The average human brain volume is 1450 cm 3 .

Figure for Exercise 11.1.2 Cross sections of the right side of the human skull. Initial figures were downloaded from http://vhp.med.umich.edu/browsers/female.html of the University of

Michigan Medical School.

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

486

Exercise 11.1.3 a. Write an integral that is the volume of the body with base the region of the x,y-plane bounded by

2/i = 0.25 v^v 7 2 – x y 2 = -0.25 ^fx </ 2 – x 0<x<2

and with each cross section perpendicular to the x-axis at x being a square with lower edge having endpoints [x, V2{x), 0] and [x,yi(x),0] (see Exercise Figure 11.1.5A). (The value of the integral is 4\/2/15).

b. Write an integral that is the volume of the body with base the region of the x,y-plane bounded by

yi = 0.25^^2-^ y 2 = -0.25 Vx <J 2 – x 0 < x < 2,

and with each cross section perpendicular to the x-axis at x being an equilateral triangle with lower edge having endpoints [x,y2(x),0] and [x, yi(x), 0] (see Exercise Figure 11.1.5B). (The value of the integral is a/6/15).

Figure for Exercise 11.1.3 Graphs for Exercise 11.1.3 The dashed lines are the lower edges of

the squares in A and triangles in B.

Exercise 11.1.4 An artist friend observes that the bodies in Figure 11.1.3 are boring and adds some pizzaz by curving the central axis with a function, w(x). Thus the base is bounded by

yx = w ( x ) +0.25v^^ 2 -x y 2 = w(x) – 0.25 y/x </ 2 – x 0<x<2.

The modified bodies are shown in Figure 11.1.4. The squares and triangles are translations of the squares and triangles in Figure 11.1.3.

a. Write an integral that is the volume of the body in Figure 11.1.4A.

b. Write an integral that is the volume of the body in Figure 11.1.4B.

Figure for Exercise 11.1.4 Graphs for Exercise 11.1.4

Exercise 11.1.5 The base of the bodies in Figure 11.1.5 are bounded by

Vl = x 2 (2 – x) y 2 = -x 2 (2 – x) 0 < x < 2.

Squares and equilateral triangles perpendicular to the axes are drawn with their lower edges spanning the base.

a. Write an integral that is the volume of the body in Figure 11.1.5A.

b. Write an integral that is the volume of the body in Figure 11.1.5B.

Figure for Exercise 11.1.5 Graphs for Exercise 11.1.5

Exercise 11.1.6 The base of the body in Figure 11.1.5 is bounded by

Hi = V 1 — x 2 2/2 = —V 1 — x 2 — 1 < x < 1.

Rectangles perpendicular to the axes are drawn with their lower edges spanning the base. The height of the rectangle at x is yl — x 2 . Write and evaluate an integral that is the volume of the body in Figure 11.1.6.

Figure for Exercise 11.1.6 Graph for Exercise 11.1.6

2 1.5

-1

Exercise 11.1.7 Find the volume of the right circular cone with base radius R and height H.

Exercise 11.1.8 The pyramid of Cheops, the largest of the Egyptian pyramids, is 146.6 meters tall with a square base of side 230.4 meters. What is its volume?

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

488

Figure for Exercise 11.1.8 Schematic diagram of the Pyramid of Cheops, Exercise 11.1.8

Exercise 11.1.9 Write as the difference of two integrals the volume of the torus (doughnut) obtained by rotating the region inside the circle x 2 + (y — b) 2 = a 2 (0 < a < b) about the rc-axis.

Exercise 11.1.10 Atmospheric density at altitude h meters is approximately 1.225e _0 ‘ 000101?l kg/m 3 for 0 < a < 5000 meters. Compute the mass of air in a vertical one-square meter column between 0 and 5000 meters.

11.2 Change the variable of integration.

If

x

define dx = g'(z) dz and write

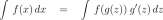
(11.4)

If a = g(c) and b

g(d), then

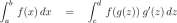
(11.5)

Example 11.2.1 For the integration problem,

substitute

x

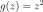
and dx = g'{z) dz = 2z dz.

Then compute

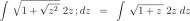
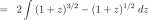
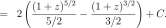
CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

489

One can remember that x = z 2 , and assume z = V% and write

/

;ii.6)

Explore 11.2.1 Check the validity of Equation 11.6.

For J ^Jl + ^/xdx, and g(z) = z 2 , g(0) = 0, and g(2) = 4.

J* ^1 + y/xdx = £ \l 1 + Vz 2 2z dz

= 2

:i + z

,5/2

:i + z

.3/2

5/2

3/2

-i 2

J 0

= 6.075895918

Proof of Change of Variables Equation 11.5. Equation 11.5 is derived from the Chain Rule for derivatives and the Fundamental Theorem of Calculus. Assume / is continuous and g has a continuous derivative and g(c) = a and g{d) = b. Suppose F and G satisfy

F\x) = f(x) and G(z) = F(g(z)).

Then G\z) = F'{g{z)) g\z) = f(g(z)) g'(z), and

f f(g(z)) g'(z) dz = f G'(z) dz = G(d) – G(c) = F(b) – F(a) = f f(x)

Jc Jc Ja

End of proof.

dx

Example 11.2.2 Problem. Compute / y/1 + x 2 dx.

Solution. Let x = teaiz. Then dx = sec 2 zdz. Compute

J \Jl + tan 2 z sec 2 zdz =

f^zdz = /(sec) (l+t»a’z)dz

r (secz) (sec z + tan z) ( r

/ h / tan z secz tan zdz

J sec z + tan z \J

sec z + sec z tan z tan 2 + sec z

u = tan z, v’ = sec z tan z

(is + sec z tan z — / sec z sec z o?^

^sec z tan z — J = \n(t&n z + sec z) + sec z tan z — J sec 3 z dz

2 J sec 3 zdz = \n(tan z + sec z) + sec z tan z + C

( 1

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

490

The following triangle helps translate from z back to x.

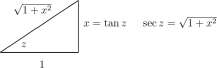
Example 11.2.3 Bacteria. A micrograph of rod-shaped bacilli is shown in Figure 11.4A. The solid, S, obtained by rotating the graph of y = b^/x^/a — x, shown in Figure 11.4B reasonably approximates the shape of the bacilli. We compute the volume, V, of S.

Figure 11.4: Rod-shaped bacilli; it Pseudomonas aeruginosa provided to Wikipedia Commons by Janice Haney Carr of the Centers for Disease Control and Public Health’s Public Image Library. B. The graph of y = b^fx\/a — x. The solid obtained by rotating the graph about the x-axis approximates the body of the bacilli.

ra . . 2

V = J 7T \ b-\fx\/a — xj dx

10

ra

= Tib 2 I y/xy/a — x dx Jo

Let x = az; then dx = adz and x = 0 and x = a correspond to z = 0 and z = 1. Then V = nb 2

/ \fa~z yja — az adz = ixb 2 a 2 \ \fz \/\ — z dz Jo Jo

The skies darken and lightning abounds.

z v 1 — z dz = — arcsin vz Wzyl — z(l — 2z) + C

4 4

Then

11.7)

V = 7Tb Z

arcsin \fz — \fz y/l — z (1 — 2z)

Equation 11.7 may be found in a table of integrals and is derived using substitution and Equation 11.4.

Problem. Find J y/z y/\ — z dz.

Solution. Let z = sin 2 9. Then dz = \ sin 2 9 1 d9 — 2 sva.9 cos 9 d9.

j y/z^l-zdz = J \jsin 2 9^1- sin 2 9 x 2sin# cos9d9 = 2 J sin 2 9 cos 2 9 d9 = – J (1 – cosA9) d9 = – – – sin40) + C = 1 (9 – (sin9cos9)(l-2sin 2 9))+C

I i

– arcsin \fz — – \fz \J\ — z(l — 2z) + C

The following triangle helps translate from 9 to z.

^fz = sin 9 cos 9 = \f\

s/T^z

Exercises for Section 11.2, Change the variable of integration.

Exercise 11.2.1 Use the suggested substitutions to compute the antiderivatives. Also, use technology or look up the integrals in a table of integrals.

a. f i dx x = sinz b. f 7 dx x = tanz

J J 1 + x 2

c. / -, = dx x = tan z d. / , = dx x = z — 1

x

e. / y/l — x 2 dx x = sin z f. / -, = dx x

Vx 2 — 1

g. / -— dx x = z 2 h. / | x = z 2

l + Vx ‘ 1 + Vx

11.3 Center of mass.

sec z

Center of mass is an important concept to students of biomechanics, the study of the movement of animals including walking, running, skating, diving. For an ice skater who performs a jump, the

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

492

path of her center of mass will be a parabola. The center of mass of a walker moves up and down with each stride, thus expending energy; the minimum energy per distance traveled is expended when walking approximately 3 mph 1 . In walking the center of mass reaches its highest point at the center of the stance (when the two feet are together) and in running the center of mass reaches its lowest point at the center of the stance 2 .

Explore 11.3.1 Through what point of a potato might you push a slender rod so that the potato would be balanced on that rod? m

If a collection of masses mi, m2, • • •, m„ is distributed at positions x\, x 2 , • • •, x n along a rod (of negligible mass) and c is a point of the rod, then the moment of the masses about c is

Moment = m 1 (x 1 – c) + m 2 (x 2 – c) H h m„_i (rr n -i – c) + m n (x n – c) (H-8)

mi m 2

m k

I

m.

x x

x 2

A

c

Xn—l

X r

The value of c for which the moment is zero is the center of mass of the system. We write the moment from Equation 11.8 equal to zero and solve for c.

n

m k (x k – c) = 0

k=l

n n n n

m k x k – m k c = m k x k -c m k = 0

k=l k=l k=l k=l

n

J2 m kXk C = *=*

k=l

Assume a mass is distributed in a region R and that the density of the mass varies along an axis L as S(x) for a < x < b. Assume also that the area of the cross section of R perpendicular to L at x is A(x) and c is a station on L. Then the moment of the mass about c is

rb

Moment of mass = / (x — c)5{x)A(x) dx. (H-9)

J a

The value of c for which the moment is zero is

rb

/ x5{x)A{x) dx

J a

f 5{x)A{x)

J a

(11.10)

t dx

lr Y. F. Novochcck, Gait and Posture, 7 (1998), 77-95

The number c in Equation 11.10 is called the center of mass of the system. If 8(x) = 5, a constant, then

b rb rb

x5A{x) dx 5 xA(x) dx / xA(x) dx

a J a Ja.

b rb rb ‘

5A(x) dx 5 A(x) dx / A(x) dx

J a J a

‘M.il)

and c is called the centroid of the region R.

Example 11.3.1 Problem. Compute the centroid of the right circular cone of height H and base radius R. See Figure 11.5

0

Figure 11.5: Centroid of a right circular cone of height H and base radius R. The conical axis lies on the X-axis.

Solution. We picture the cone as the solid of revolution obtained by rotating the graph of y = (R/H) x x, 0 < x < H about the X-axis. Then A(x) = n x ( (R/H) x ) 2 and the centroid c is computed from Equation 11.11 as

rH rH

I x-k x ( (R/H) x ) 2 dx I x 3 dx jj 4 ^ 3

n x ((R/H)x) 2 dx / x 2 dx n /J 0 Jo

The centroid, c, is 3/4 the distance from the vertex of the cone and 1/4 the distance from the base of the cone. ■

Example 11.3.2 Problem. Suppose a horizontal flat plate of thickness 1 and uniform density has a horizontal outline bounded by the graph of y = x 2 , y = 1, and x = 4. Where is the centroid of the plate. See Figure 11.6.

Solution. There are two problems here. The first is, ‘What is the x-coordinate, x, of the centroid’; the second is, ‘What is the y-coordinate, y, of the centroid?’ The z-coordinate of the centroid is one-half the thickness, z — 1/2.

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

494

10 12 14 16

Figure 11.6: Centroid of a horizontal flat plate bounded by the graphs of y = x 2 , y = 0, and x = 4.

For the x-coordinate of the centroid, the cross sectional area of the region in a plane perpendicular to the X-axis at a position x is x 2 x 1 = x 2 for 0 < x < 4. We write

x

x x x 2 dx

0u didC

x 3 dx

4 4 /4 473

For the y-coordinate of the centroid, the cross sectional area of the region in a plane perpendicular to the F-axis at a position y is (1 — ^/y) x 1 = 1 — ^fy for 0 < y < 16. We write

16 _ /-16

y x (1 – y/y)dy / y – y 3/2 dx

y 2 /2 – y 5/2 /(5/2)

16

1 – yfjjdy

16

iy l ‘ 2 dx [y-y 3/2 / ‘(3/2)

16 0

24

Example 11.3.3 Problem. Consider a hemispherical region generated by rotating the graph of y = vl — x 2 , 0 < x < 1 about the x axis that is filled with a substance that has density, 5(x), equal to x. Find the center of mass of the substance.

Solution. At position x, the radius of the cross section perpendicular to the X-axis is y/l — x 2 , the area of the cross section is 7r(l — x 2 ). From Equation 11.10, the

Center of mass

xS(x)A(x) dx / x x x x 7r(l — x 2 ) dx

6(x)A(x) dx

x 2 — x 4 dx x — x 3 dx

x x 7r(l — x ) dx

x 3 /3 – x 5 /5

x 2 /2 – x 4 /4

8

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

495

Exercises for Section 11.3, Center of Mass

Exercise 11.3.1 Find approximately the horizontal coordinate of the center of mass of the potato shown in Figure 11.1 using the data

Slice Position (cm) 2 4 6 8 10 12 14 16 Slice Area (cm 2 ) 11 15 14 16 17 15 13 10

The next two problems require evaluation of some integrals. You may find your calculator or MATLAB useful. The Texas Instrument calculator command “fnlnt” is useful. To integrate 3 * x 1 5 — rr 2 5 from x = 2 to x = 3, for example, you would push 2nd calc and find fnlnt. Then write fnlnt (3*x~ (1.5)-x~ (2.5) ,x,2,3).

Or you may use MATLAB. Write an m-file, say, myfun6.m

function y = myfun6(x) y=3*x.~1.5 – x.~2.5;

Then issue the command, Q = quad(@myfun6,2,3)

Exercise 11.3.2 Find the x-coordinate of the centroids of the areas:

a. The triangle with vertices (0,0), (2,0) and (2,1); 0 < x < 2, 0 < y < 0.5 x x.

b. The semicircle, 0 < x < 1, — x 2 < y < \Jl — x 2 .

c. The parabolic segment, 0 < x < 1, — \fx <y< \fx.

d. The parallelogram with vertices (0,0), (1,1), (3,1), and (2,0).

Exercise 11.3.3 For 1 cm thick plates that have plans in the x-y plane described below, suppose the the density at position x is 2 x y/x. Find the x-coordinates of the centers of mass of the objects. If there is an integral for which you can not find an appropriate antiderivative, use your technology or approximate the integral using 10 subintervals of the interval of integration.

a. The triangle with vertices (0,0), (2,0) and (2,1); 0 < x < 2, 0 < y < 0.5 x x.

b. The semicircle, 0 < x < 1, —y/l — x 2 < y < y/l — x 2 .

c. The parabolic segment, 0 < x < 1, — y/x < y < \fx.

d. The parallelogram with vertices (0,0), (1,1), (3,1), and (2,0). Danger: Evaluation of the six integrals by hand without error is highly improbable. You should write the integrals and accept our answer: 1.6531.

Exercise 11.3.4 Find the centroid of that portion of the sagittal section of the skull shown in Exercise Figure 11.3.4 that lies above a line connecting the two circles. Scale of the figure is 1:4.

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM 496 Figure for Exercise 11.3.4 Sagittal section of a human skull at 1:4 scale, Exercise 11.3.4.

o

o

11.4 Arc length and Surface Area. Arc Length.

Consider the problem of finding the length of the graph of y = f(x) shown in Figure 11.7.

(X -‘ y -> (x,yj

l l l l l l l l_

Figure 11.7: Graph of a function, /, and a polygon that approximates it.

We partition the interval [a, b] into a = x 0 < X\ < ■ ■ ■ < Xk-i < Xk < ■ ■ ■ x n = b. Then the length of / is approximately

Length = \J(x k – x^) 2 + (f(x k ) – f(x k _ l )) 2 k=l

k=l \

j + / f{Xk) -/(gfc-i) V \ X k ~ X k -i J

(x k – X k -i)

By the Mean Value Theorem, for each k there is a number c k between x k -\ and x k such that

f(xk) – f(xk-i)

f'(c k ).

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

497

Then

n .

Length = V 1 + U'( c k)) 2 (x k – x k -i) k=i

This pattern fits Definition 9.4.4, Definition of Integral II, and

£ yf\ + (f'(c k )) 2 (x k – Xfc-x) = / y/l + (f'(x)) i i Jo,

b

2 dx

k=l

Both approximations converge as the norm of the partition decreases to zero and we write

Length of the graph of / is f Jl + (f'(x)) 2 dx (H-12)

J a

Equation 11.12 is excellent in concept but difficult in practice in that there are not many

functions / for which an antiderivative / y 1 + ( f'(t) ) 2 dt can be found. One function for which the antiderivative can be found is y = In cos a;.

Example 11.4.1 Problem. Find the length of the graph of y = In cos a; on 0 < x < 7r/4. We write

fix) = In cos a; f (x) — [lncosxl’ Fcosxl’ = ( — cos a;) = — tan a;

Jy 1 J cosa; L J cosa; v 1

We leave it to you to check that Bolt out of the Blue

[ ln(sec x + tan x) ]’ — sec x

We can write

rn/4 j /”7r/4 / r7v/A

Length = j y 1 + (f'(x)) 2 dx = J \fl+t&n 2 xdx = J sec dx = [ ln(sec x + tan x)

= ln(sec(7r/4)+tan(7r/4))-ln(sec(0)+tan(0)) = 0.881 ■

Surface Area. The surface area to volume ratio limits the size of cells. The surface areas of the lungs and the small intestine determines, respectively, the oxygen absorbance and nutrient absorbance in humans.

We will compute surface areas only for surfaces of revolution. We use the fact that the surface area of the frustum of a cone (illustrated in Figure 11.8A) is

Area of frustum of a cone = n(ri + r 2 ) si

The proof is left to you, and you may be assisted by Figure 11.8B in which the frustum has been cut along a slant side and flattened. The angle 9 = 2irr 1 /(s 1 + s 2 ) = 27rr 2 /s 2 –

Shown in Figure 11.9 is a surface of revolution and a section between x k ^\ and x k . The area of that frustum is

A k = n(f(x k -i + f(x k ))y/(x k – Xk-i) 2 + (f(x k ) – f(x k -i)) 2 = 7r(/(x fc _i + f(x k ))

, ( f( X k) ~ f(X k -l)\ 2 , V

1 + [X k – Xfc_i)

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

498

Figure 11.8: A. The frustum of a cone; ri, r2, and hi determine the cone. B. The same frustum flattened onto a plane. The angle 9 = 2nri/(si + S2) = 27rr2/s2-

f <Vi>

Figure 11.9: A surface of revolution with approximating conical frustum.

By the Mean Value Theorem there is a number, c k between Xk-i and x k such that

The area of the surface of revolution is approximately J2k=i ^-k so that

Surface Area = 7r(/(x fc _i) + f{x k ))\/l + (f'(c k )) 2 (x k – x k -i)

Because x k -i, c k and x k may all three be different, we appeal to an even more general definition of the integral than Definition of the Integral II and conclude that this approximating sum converges

to f a n(f(x) + f(x))yl + ( f'(x) ) 2 dx. as the norm of the partition goes to zero. Therefore we write

Surface Area = t 2irf(x)Jl + (f'(x) ) 2 dx (11.13)

J a

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

499

Again the collection of functions / for which an antiderivative / 271″/(a;) y 1 + ( fix) ) 2 dx can be found is small. Fortunately one such function is fix) = \/R 2 — x 2 and the surface area is that of a sphere, 4tcR 2 , which appears in Exercise 11.4.4.

Exercises for Section 11.4, Arc Length and Surface Area. Exercise 11.4.1 Find the length of the graph of fix) = § x 2 ^ 3 , 1 < x < 8. Note: In order to

evaluate the integral, use a substitution, = x 2//3 + 1, u\x Exercise 11.4.2 Write an integral that is the length of the curve

e x + e~ x

2 -1/3 3 x

y

Kx<l.

Show that the integral is J_ 1 yix) dx and evaluate it.

The graph of y is the shape of a cable suspended between the points (— l,y(— 1)) and (l,y(l)) and is called a catenary.

Exercise 11.4.3 a. Find the length of the spine illustrated in Figure 11.4.3.

b. The spinal chord begins at the occipital bone and extends to the space between the first and second lumbar vertebrae. Find, approximately, the length of the spinal chord.

, -10 cm

-5

Figure for Exercise 11.4.3 H -0

Spinal Chord. This is a figure from Gray’s Anatomy, colored and put into the public domain by Uwe Gille. See http://en.wikipedia.org/wiki/Spinal_cord.

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

500

Exercise 11.4.4 Use Equation 11.13 and f(x) = \JR 2 — x 2 to find the surface area of a sphere of radius R. Archimedes knew this to be AtiR 2 . He first guessed the answer based on the common knowledge among basket weavers that the bowl of a hemispherical basket required twice as much material as its top, which has area nr 2 .

Exercise 11.4.5 Find the area of the surface generated by rotating the graph of y = 2y/x, 0 < x < 1 about the x-axis.

Exercise 11.4.6 How much glaze on a doughnut? Write as a sum of two integrals the surface area of the torus (doughnut) generated by rotating the circle x 2 + (y — b) 2 = a 2 (0 < a < b) about the x-axis. Note: The surface area is Aabrc 2 .

11.5 The improper integral, f%° f(t)dt.

In this section we give examples of problems for which a reasonable answer is of the form

lim / f(t)dt which is denoted by / f(t) dt (H-14)

R^co J a J a

This is called an ‘improper’ integral, but there is nothing improper about it. Another integral

/ -j=dx, Jo \JX

is also said to be improper. The integrand, -4= has an identity crisis at x = 0: the integrand is not

\/x

defined at x = 0 and is unbounded in every interval [0,r], r > 0. The integrand is continuous on every interval (r, 1], r > 0, however, and

1 1 r 1 1

—j= dx is defined to be lim / —= dx = lim

2y/x

1

2.

Example 11.5.1 Problem. Is there an initial vertical speed of a satellite that is sufficient to insure that it will escape the Earth’s gravity field without further propulsion? Solution. The work done along an axis against a variable force F(x) is

W = f b F(x) dx

J a

The acceleration of gravity at an altitude x is given as

R 2

g(x) = 9.8 x -J meters/sec 2

(it + x)

where R = 6370 meters is the radius of Earth. This means a satellite of mass m and altitude x experiences a gravitational force of

R 2

Fix) = m x 9.8 x — Newtons

v ; (R + x) 2

The work required to lift the satellite to an altitude A is

r A R 2 r A 1

W(A) = m x 9.8 x -~dx = 9.8 x m x R 2 / –

v ; Jo (R + x) 2 Jo (R + x)

The integral is readily evaluated.

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

501

Earth

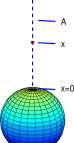
Figure 11.10: Vertical path of a satellite from Earth. The gravitational force on the satellite at height, x, is F(x) = g R 2 / (R + x) 2 m/sec 2 .

Explore 11.5.1 Show that

W(A) = 9.8 x m x R 2

1 1

R ~ (R + A)

How much work must be done to send the satellite ‘out of Earth’s gravity field’, so that it does not fall back to Earth? This is

lim W(A)

lim 9.8 x m x R

A-^oo

R (R + A)

9.8 x m x R

A finite amount of work is sufficient to send the satellite out of the Earth’s gravity field.

Now suppose we neglect the friction of air and ask at what velocity should the satellite be launched in order to escape the Earth? We borrow from physics the formula for kinetic energy of a body of mass m moving at a velocity v.

Kinetic energy = -mv 2 . Then we equate the kinetic energy with the work required

1 9

-mv = 9.8 x m x R, 2

and solve for v. The solution is

v = \/2R x 9.8 = 11,174 meters per second

A satellite in orbit travels about 7,500 m/sec. The muzzle velocity of a rifle is about 1,000 m/sec. ■

Example 11.5.2 The mean and standard deviation of an exponential life table. Consider first a finite life table:

An animal population is established as newborns; 4 tenths of the population die at age 1 (perhaps harvested), 3 tenths of the population die at age 2, 2 tenths of the population die at age 3,

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

502

Figure 11.11: Life table and graph. D(x) is the fraction of the original population that dies at age x and L(x) is the fraction of the original population that live until age x.

and 1 tenth of the population die at age 4. The data may be organized as in Figure 11.11. We define D(x) to be the fraction of the original population that dies at age x and L(x) to be the fraction of the original population that live until age x. The life expectancy, or average age at death, is

A = 0.4×1 + 0.3×2 + 0.2×3 + 0.1×4 = 2

D(x) x x

x=l

1

J2 ~ L{x + 1)) x x

2 = 1

For a general life table, L, with data points xo,x\,X2, ■ ■ ■ ,x n , (and L(x n ) = 0) the life expectancy is

A = xi (L(x 0 ) – L(xi) + x 2 {L{xx) – L(x 2 ) H \-x n (L(x n _i) – L(x n )

If L is a differentiable approximation to a life table defined on an interval [0,6] (with L(b) = 0) and {xk}^ =0 is a partition of [0,6], then

i ti it, pfo

A = Y,{ L { x n-i)-L(x n ))-x n = Y, x n{-L'{c n ))(x n -x n ^ 1 )= / x(-L'(x))dx

k=l k=l J °

where L(x n ^i) — L(x n ) = —L'(c n ) [x n — x n _i) by the mean value theorem. The average age determined by L is

A = – / xL'(x)dx (11.15) Jo

It is often assumed that a life table can be approximated by a negative exponential of the form

L(x) = e~ Xx where b = oo in Equation 11.15

Then

i-R poo

Average age at death =— lim / x (— \e~ Xx ) dx = X / xe~ Xx dx

R^oc Jo Jo

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

503

Explore 11.5.2 Use integration by parts to show that

/

x x e Xx dx = — -xe Xx A

-Aa;

A 2

+ c

Therefore, the average age at death is

= A / xe Xx dx Jo

A lim

R— >oo

xe’ Xx /X – e~ Ax / A

Xx l\2

x=R x=0

A lim

-Re~ XR /\ – e~ XR /\ 2 + 1/A 2 J = 1/A By similar reasoning, the standard deviation of the age at death in the population is

roo

A / (x- 1/A) 2 x e~ Xx dx Jo

Explore 11.5.3 Use two steps of integration by parts to show that

f(x- l/X) 2 eXx dx = -(x- 1/A) 2 (eA 7A) – 2{x – 1/A) e A 7A 2 – 2e” A 7A 3 ■

In Exercise 11.5.8 you are asked to show that

X (x-l/\) 2 xeXx dx = l/\ 2 m Jo

(11.16)

(11.17)

Exercises for Section 11.5, Improper Integrals. Exercise 11.5.1 Show that

roo I [R I

dx

[ —„dx = lim / — Ji x a R^oo Ji x a

is finite if 1 < a and is infinite if 0 < a < 1. Exercise 11.5.2 Show that

r 1 1 f 1 1

/ — dx — lim / —- dx

J0 X r^0+ J r X

is finite if 0 < a < 1 and is infinite if 1 < a.

Exercise 11.5.3 Compare the regions whose areas are

oo I A I

—o dx and / —= dx 1 x Jo \/X

Exercise 11.5.4 a. Show that

111 r°° 1

1 + + + < 1 + / 7 To d*.

2 2 3 2 4 2 ~ Jo (1 + t) 2

See Figure 11.5.4. b. Show that

1111

^t + ^t + ^t + ^tH < 1.5.

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

Figure for Exercise 11.5.4 Graph of y — 1/(1 + t) 2 and boxes of areas 1/2 2 ,1/3 2 ,1/4 2 ,

504

Exercise 11.5.5 a. Show that

See Figure 11.5.5. b. Show that

1 1 1 1

l + 2 + 3 + 4 + — = oo.

Figure for Exercise 11.5.5 Graph of y — 1/(1 + 1) and boxes of areas 1,1/2,1/3, • • •.

Exercise 11.5.6 Consider the infinite horn, H, obtained by rotating the graph of

y = 1/x, 1 < x about the x-axis.

See Exercise Figure 11.5.6.

a. Show that the volume of the interior of H is ir.

b. Show that the surface area of H is greater than.

f°° 1

/ 27T— dx = oo Ji x

c. H, then, has a finite volume and can be filled with paint, but has an infinite surface area and can not be painted! I enjoyed telling a very good class about this one day. The next day Mr. Jacks, a generally casual student, told me he could paint it, and he could. His grade in the course was an A. Can you paint HI

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

505

Figure for Exercise 11.5.6 An infinite horn, H, obtained by rotating the graph of y — 1/x,

1 < x about the x-axis

Exercise 11.5.7 The gamma function, T(n) = x n e x dx is an important function in the study of statistics.

a. Compute

b. Use one step of integration by parts to compute T(2).

c. Use one step of integration by parts and the previous step to compute T(3).

d. Use one step of integration by parts to show that if n is an integer, T(n + 1) = nT(n). Exercise 11.5.8 Use Equation 11.16 to establish Equation 11.17

R^oo 1 — e~ XR Jo Exercise 11.5.9 A linear life table is given by

L(x) = 1 — x/m for 1 < x < m

Find the mean and standard deviation of the life expectancy (age at death) for this life table.

Exercise 11.5.10 Wildlife managers decide to lower the level of water in a lake of 8000 acre feet. They open the gates at the dam and release water at the rate of ^+i) 2 acre_ f ee t/day where t is measured in days. Will they empty the lake?

Exercise 11.5.11 Algae is accumulating in a lake at a rate of e~ omt sin 2 -nt. The factor e~ 0 05 * reflects declining available oxygen and the factor sin 2 nt reflects diurnal oscillation. Is the amount of algae produced infinite? See Exercise Figure 11.5.11.

Figure for Exercise 11.5.11 The amount of algae produced is the area of the shaded region

(extended to t = oo). The upper curve is the graph of y = e

0.05t

Time days

CHAPTER 11. APPLICATIONS OF THE FUNDAMENTAL THEOREM

506

Exercise 11.5.12 Algae is accumulating in a lake at a rate of ^ sin 2 irt. The factor ^ reflects declining available oxygen and the factor sin 2 nt reflects diurnal oscillation. Is the amount of algae produced infinite? See Exercise Figure 11.5.12.

Figure for Exercise 11.5.12 A. The graph of y = 1/(1 + 1). B. The amount of algae produced is the area of the shaded region in B (extended to t = oo). The upper curve is the graph of

y = 1/(1 + 0-

A

B

a. Show that the area of the shaded region (extended to oo) in Exercise Figure 11.5.12 A (— Jo°° i+t dt) is infinite.

b. Show that the sum of the areas of the boxes (extended to oo) in Exercise Figure 11.5.12 A is infinite.

c. Argue that the algae production on day 1 is larger than Jq 1 | sin 2 -irt dt.

d. Argue that the algae production on day 2 is larger than J 2 | sin 2 7ri<ii.

e. Believe that for any positive integer, k,

k+l

sin 2 nt dt =

k Jk

k + l 1 – COS 2-Kt

dt

1 1 l fc+1 1

-t Sill ZTlt

2 4tt

f. Argue that

coo ~\

9 11 11 11 11

sin TTtdt> 1 1 1 h

o 1+t 22 32 42 52

1/1 1 1 1

2\2 + 3 + 4 + 5 +

g. Think of the boxes in part b. and argue that

1111

2 + 3 + 4 + 5 +

‘OO

Exercise 11.5.13 It is a fact that

Compute

[arctan x]’ = —

0 1 +x 2

dx

Chapter 12

The Mean Value Theorem and Taylor Polynomials.

Explore 12.0.4 An eagle flies from its aerie, remains in flight for 30 minutes, and returns to the aerie. Must there have been some instant in which the eagle’s flight was horizontal? ■

12.1 The Mean Value Theorem.

Theorem 12.1.1 Mean Value Theorem. Suppose / is a function defined on a closed interval [a, b] and

1. / is continuous on the interval, [a, b].

2. f'(x) exists for every number a < x < b. Then there is a number, c, with a < c < b such that

/'(c) = Hb l ~ f(a) (12.1)

Explore 12.1.1 Do this. Locate (approximately) a point on each graph in Explore Figure 12.1.1A and B at which the tangent is parallel to the secant. ■

Explore Figure 12.1.1 Graphs with secants; find points at which tangents to the graphs will be

parallel to the secants.

8 I , , , , , , , , , 1 1

The Mean Value Theorem relates an average rate of change to a rate of change. It is surprisingly useful, despite there being uncertainty about the number c asserted to exist.

Uncertainty: Suppose a motorist travels on a turnpike which is 150 miles between the entry and exit, and the ticket records that it was 1:20 pm on entry and 3:20 pm on exit. The operator at the exit observes that the motorist was speeding, and the motorist protests that he never exceeded the 70 mph speed limit. The operator looks the car over and responds, “I see no evidence of possible discontinuous motion (as might occur in extra-terrestrial vehicles) and I am certain that at some time during your trip you were traveling 75 mph.” His reasoning is that the average speed was 75 mph so there must have been an instant at which the speed was 75 mph. He cannot say exactly when that speed was attained, only that it occurred between 1:20 and 3:20 pm.

Example 12.1.1 In special cases, we can actually find the value of c.

The Mean Value Theorem asserts that there is a tangent to the parabola y 2 = x that is parallel to the secant containing (0,0) and (1,1). Let

f(x) = \fx 0 < x < 1.

See Example Figure 12.1.0.2A.

Figure for Example 12.1.0.2 A. Graph of f(x) = ^Jx and the secant through (0,0) and (1,1) B.

The tangent at (1/4, 1/2) is parallel to the secant.

0 0.5 1 o 0.5 1

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

509

The function, / is continuous on the closed interval [0,1] and

/'(*)

1 _1 1

-x 2 = —_ 0 < x < 1

2 2^x

The parabola has a vertical tangent at (0,0) and /'(0) is not defined. Even so, the hypothesis of the Mean Value Theorem is satisfied; the requirement is that f'{x) exist for 0 < x < 1 – only required for points between 0 and 1.

We seek a tangent parallel to the secant through (0,0) and (1,1); the secant has slope

•^^-j _ = 1, so we look for a tangent of slope 1.

The Mean Value Theorem asserts that there is a number c such that f'{c) = 1. We solve for c

in

f'(c) = 1 A= = 1 ~ = Vc c=A . Also, / (-) = –

The tangent to / at (1/4, 1/2) has slope 1 and is parallel to the secant from (0,0) to (1,1) (Example Figure 12.1.0.2B.) ■

We will find good uses for the Mean Value Theorem in the next section. First, though, we tend to its proof. The strategy is to prove a special case where f(a) = f(b) = 0, called Rolle’s Theorem, published by the French mathematician Michel Rolle in 1691. Then a proof of the general theorem is easy.

In Theorem 8.2.1 on page 351 we showed that for an interior local maximum, (c, /(c)), if the graph of / has a tangent at (c, /(c)) then that tangent is horizontal. The same assertion applies to interior local minima. See Figure 12.1

Figure 12.1: The tangents to interior local minimum and maxima are horizontal.

Theorem 12.1.2 Rolle’s Theorem. If a function, /, defined on a closed interval, [a, 6], satisfies

1. f(a) = f(b).

2. / is continuous on [a, b].

3. /'(c) exists for every number c, a < c < b.

then there is a number c between a and b for which /'(c) = 0.

(u,f(u))

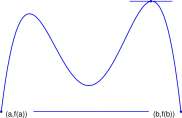
Figure 12.2: Graph with interior maximum (and endpoint minimum).

The proof is seemingly harmless. We are looking for a horizontal tangent and therefore only have to look at a high point (u, f(u)) and a low point (v, f(v)) of / on [a, b].

If a < u < b, as in Figure 12.2, then (u, f(u)) is an interior local maximum and the tangent at (u, f(u)) is horizontal. Choose c = u. Then f\c) = 0.

Similarly, if a < v < b, (v, f(v)) is an interior local minimum, the tangent at (v, f(v)) is horizontal. Choose c = v. Then f'(c) = 0.

If u and v are both end points of [a, b] (meaning u is a or b and v is a or b) then for x in [a, b], because f(a) = fib), the largest value of f(x) is f(a) = fib) and the least value of f(x) is f(a) = fib) so the only value of f(x) is f(a) = f(b). See Figure 12.3. Thus the graph of / is a horizontal interval and every tangent is horizontal. For the conclusion of the theorem we can choose c any point between a and b and f\c) = 0.

u = a c v = b • 1 •

v = a

Figure 12.3: Graph with endpoint minimum, and endpoint maximum, u and v may be the same endpoint or at opposite ends of [a, b}.

A weakness in the preceding discussion is the presumption that the graph of / has a highest point. Under the assumptions of Theorem 12.1.2, / is continuous at every number in [a, b], and there is a theorem that the graphs of such functions have high points (and low points). We ask you to accept the following theorem as true.

Theorem 12.1.3 High Point Theorem. If / is a continuous function defined on a closed interval, [a, b], then there is a number c in [a, b] such that for all x in [a, b], f(x) < /(c).

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

511

We ask that you accept the High Point Theorem as true without proof. It is interesting that the High Point Theorem may be used as an alternative to the Completion Axiom 5.2.1 as an axiom of the number system (see Exercise 12.1.10). With the High Point Theorem accepted as true, the proof of Rolle’s Theorem is complete. End of Proof.

Example 12.1.1 The function, /, defined by

,/ x _ J 0 for x = 0 JW – i i f 0 < x < 1

K x —

is defined on [0,1] but does not have a highest point; nor is / continuous. See Figure 12.4 ■

100

Figure 12.4: The graph of /(0) = 0, f(x) = l/x for 0,x < 1.

Example 12.1.2 Rolle’s Theorem is useful in showing some functions are invertible. Let F be the function defined by F(x) = x + x 3 for all numbers, x. We will show that no horizontal line intersects the graph of F at two distinct points, which means that F is invertible. Observe that

F'(x) = [x + x 3 }’ = 1 + 3x 2 > 0 for all x.

By Rolle’s Theorem, if some horizontal line contains two points of the graph of F then at an intervening point there is a horizontal tangent and at that point F’ = 0. This is impossible because F'(x) = 1 + 3x 2 > 0 for all x. Thus F is an invertible function. ■

Proof of the Mean Value Theorem. Suppose / is a continuous function on an interval [a, b] and f'(t) exists for a < t < b. An equation of the secant line through (a, /(a)) and (b, f(b)) is

L(x) = f(a) + f{b) ~ f{a \ x-a) b — a

Let D(x) = f(x) — L(x). Then D is the difference between two continuous functions, / and L, that have derivatives between a and b, so D is continuous and has a derivative between a and b. Furthermore

D(a) = f(a) – (f(a) + M Z ^ ( a _ a )\ = 0

and

D(b) = f{b) – (f(a) + /( ^” /(Q) (6 -a))=0

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

512

(These zeros are not a surprise because / and the secant intersect at (a, f(a)) and (b, f(b)).)

Therefore D satisfies the hypothesis of Rolle’s Theorem so there is a number c, a < c < b, such that D'(c) = 0. Now

D'(x) =

and D'(c) = 0 leads to

!(x) -{ !{a)+ m^m (x a )

[/(*)]’ -!/(«)]’

b — a

fib) – f(a) b — a

(x — a)

= f'(x)-0

f(b) – M b — a

D'(c) = f(c)-

o = m-

m – m

b — a fib) – f(a)

b — a

f'(c) =

f(P)-M

b — a

which is the conclusion of the Mean Value Theorem. End of proof.

Exercises for Section 12.1, The Mean Value Theorem.

Exercise 12.1.1 For each of the functions, F, draw a graph of F and the secant through (a, F(a)) and (b, F(b)) and a tangent to the graph of F that is parallel to the secant.

a. F(x) = i [a, b] = [1/2,2] b. F(x) = [«,&] = [-1,1]

c. F(x) = e x , [a,b] = [0,2] d. F(x) = sinx, [a,b] = [0,tt/2] Exercise 12.1.2 For f(x) = x 2 + x find a value of c for which

ffl=M and 0<c<2

Locate the point (c,/(c)) on the graph in Ex. Figure 12.1.2 and draw its tangent. Compute f'(c).

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

513

0 12 4 6

Exercise 12.1.3 Find a number c between a and b for which f'{c) = f(b) — f(a)/(b — a).

Exercise 12.1.4 Show that the following functions are invertible.

a. F(t) = e* b. F(t) = tant, -f < t < f

c. F(t) = Int, 0<t d. F(t) = \/5^t, t<5 Exercise 12.1.5 The graph of the function F defined by

F(x) = v^x 2

is shown in Figure 12.1.5 together with the secant to the graph through (-8,4) and (2,4 1//3 ). Is there a tangent to the graph at a point between (-8,4) and (^^A 1 ^ 3 ) that is parallel to the secant between these two points? Does the Mean Value Theorem assert that there is such a tangent? Explain your answer.

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

514

Exercise 12.1.6 The graph of the function / defined by

is shown in Figure Ex. 12.1.6. It does not have a high point. Furthermore, it does not have a horizontal tangent; yet it satisfies all but one of the hypotheses of Rolle’s Theorem. Which hypothesis of Rolle’s Theorem does it not satisfy?

Figure for Exercise 12.1.6 Graph of Equation 12.2.

_ 0 .2 1 1 ‘ 1 1 ‘ 1 1

-0.2 0 0.2 0.4 0.6 0.8 1 1.2

Exercise 12.1.7 . Draw the graph of a continuous function F with domain [1,5] that has a non-negative derivative at every point between 1 and 5, and for which 5 is a local minimum.

The next three exercises demonstrate interesting function equivalents of the Axiom of Completeness 5.2.1 from Section 5.2.

Axiom of Completeness If Si and S2 are two sets of numbers and

1. Every number belongs to either Si or S2, and

2. Every number of Si is less than every number of S2,

then there is a number C such that C is either the largest number of Si or C is the least number of S2.

Exercise 12.1.8 Complete the proof of Theorem 12.1.5.

Theorem 12.1.4 Intermediate Value Theorem If / is a continuous function with domain an interval [a, b], and f(a) < 0 and f(b) > 0 then there is a number c between a and b for which f(c) = 0.

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

515

Theorem 12.1.5 If the usual properties of addition, multiplication and order of the number system are assumed, one may accept the statement of the Intermediate Value Theorem 12.1.4 as an axiom and prove the statement of the Axiom of Completeness Axiom 5.2.1 (repeated above) as a theorem.

Proof. Assume the usual properties of addition, multiplication, and order of the number system and the statement of the Intermediate Value Theorem. Suppose the statement of the Completion Axiom is not true. Then there are sets of numbers, Si and S 2 such that every number is in either Si or S2 and every number of Si is less than every number in S2 and Si does not have a largest number and S2 does not have a least number.

Let a be a number in Si and b be a number in S 2 . Consider the function / defined on [a, b] by

!—1 for a < x and x in Si (12.3) 1 for x < b and x in S 2

Exercise 12.1.9 Prove Theorem 12.1.6:

Theorem 12.1.6 If the usual properties of addition, multiplication and order of the number system are assumed, one may accept the statement of the High Point Theorem 12.1.3 as an axiom and prove the statement of the Completion Axiom 5.2.1 as a theorem.

Exercise 12.1.10 Prove Theorem 12.1.6:

Theorem 12.1.7 If the usual properties of addition, multiplication and order of the number system are assumed, one may accept the statement of Rolle’s Theorem 12.1.2 as an axiom and prove the statement of the Completion Axiom 5.2.1 as a theorem.

12.2 Monotone functions; second derivative test for high points.

With the Mean Value Theorem we can easily prove three results left from Sections 8.1 and 8.2.1. In Section 8.1 we stated that we would prove:

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

516

Theorem 12.2.1 Suppose P is a continuous function denned on an interval [A, B] and at every point * in (A, B) P'(t) exists and P'(i) > 0. Then P is nondecreasing on [A, B].

Proof. Suppose a and b are numbers in [A, B] and a < b. Then by the Mean Value Theorem, there is a number, c, between a and b such that

By hypothesis, P'(c) > 0. Also a < b so that b – a > 0. It follows that P(b) – P(a) > 0, so that P(a) < P{b). Therefore P is nondecreasing on [A, B]. End of proof. We also stated in Section 8.1 that we would prove:

Proof: The argument is the similar to that for Theorem 8.1.1 and is left as Exercise 12.2.3

There are obvious corollaries to Theorem 12.2.1 (P’ < 0 implies P is nonincreasing) and Theorem 12.2.2 (P’ < 0 implies P is decreasing).

Example 12.2.1 Theorems 12.2.2 and its corollary can be used in the following way. Problem. Let P(x) = 3x 4 – 20x 3 – 6x 2 + QOx – 37. On what intervals is P increasing? On what intervals is P decreasing? Solution. We compute

P\x) = I2x 3 – 60x 2 – Ylx + 60 = 12(x 3 – 5x 2 – x + 5) = 12(x + l)(x – l)(x – 5)

Confession. P(x), was selected so that the cubic, P'(x), would factor nicely.

Now P'(— 1) = -P'(l) = P'(5) = 0 which suggests that -1, 1, and 5 might be x-coordinates of local maxima and minima. We form a chart:

P(b) – P(a)

so that P(b) – P(a) = P'(c)(b – a)

b — a

Theorem 12.2.2 Suppose P is a continuous function defined on an interval [A, B] and at every point t in (A, B) P'(t) exists and P'(t) > 0. Then P is increasing on [A, B\.

(-)(-)(-)

(+)(-)(-)

(+))(+)(-)

(+)(+)(+)

-1

1

5

P’ < 0

P’ > 0

P’ < 0

P’ > 0

The chart means that for x < —1 the three binomial factors in P’ = 12(x + l)(x — l){x — 5) are all negative so that P’ is negative for all x < — 1. This means that P is decreasing through out

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

517

(—00, —1). By similar reasoning, P is increasing on (—1,1), decreasing on (1,5) and increasing on (5,oo).

We evaluate P at three (critical) points.

P(-l) = 3(-i) 4 _20(-l) 3 -6(-l) 2 + 60(-l)-37=-80 P(l) = 0 P(5) = -512

These three points are plotted on the graph in Figure 12.2.0.2 and arrows indicate the increasing and decreasing character of P between the data points. A candidate for the graph of P could be drawn with just this information. In fact, the dashed line in Figure 12.2.0.2 is the graph of P ■

Figure for Example 12.2.0.2 The points (-1,-80), (1,0), and (5,-512) are plotted with arrows showing the increasing and decreasing character of P(x) = 3x 4 — 20a; 3 — 6x 2 + 60s — 37 on the intervals between the data points. The dashed line is the graph of P.

-2-1 0 1 2 3 4 5 6

The second derivative test. In Section 8.2.1 we stated the second derivative test:

Theorem 12.2.3 Suppose / is a function with continuous first and second derivatives throughout an interval [a, b] and c is a number between a and b for which f'(c) = 0. Under these conditions:

1. If /”(c) > 0 then c is a local minimum for /.

2. If /”(c) < 0 then c is a local maximum for /.

Proof. We prove case 1, for c to be a local minimum of /. It will be helpful to look at the numbers on the number lines shown in Figure 12.5. Because /” is continuous and positive at c, there is an

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

518

interval, (u,v), containing c so that /” is positive throughout (u, v) 1 . See the top number line in Figure 12.5. Suppose x is in (u,v) (the second number line in Figure 12.5). We must show that

f(c) < /(.<•).

We consider the case x < c.

I

u I

u

I

X

I

u

X

Cl

u

X

Cl

c 2

Figure 12.5: Number lines for the argument to Theorem 12.2.3.

By the Mean Value Theorem, there is a number, c\ between x and c for which f(c) – /(*)

c — X

/'(ci) so that /(c) – /(x) = /'(ci)(c – x)

(12.4)

See the third number line in Figure 12.5.

Watch this! By the Mean Value Theorem applied to the function /’ and its derivative /”, there is a number c 2 between c\ and c so that

f'(c) – /'(d)

C — Ci

= /”(c 2 ) and / / (c)-/'(c 1 ) = /”(c 2 )(c-ci)

(12.5)

See the bottom number line in Figure 12.5.

Remember that /'(c) = 0 so from the last equation (Equation 12.5)

/'(ci) = -/”(c 2 )(c-ci)

and from this and Equation 12.4 we get

f(c)-f(x) = -f”(c 2 )(c-c 1 )(c-x)

Now Ox and c > c\ so that c — x and c — c\ are positive. Furthermore, /”(c 2 ) > 0 because /” is positive throughout (u,v). It follows that /(c) — f(x) is negative, and that /(c) < /(#). The event c < a; is similar.

The argument for Case 2. of Theorem 12.2.3 is similar. End of proof.

Exercises for Section 12.2, Nondecreasing and increasing functions; second derivative

test for high points.

Exercise 12.2.1 Show that the following functions are invertible.

a. fix) = x 2 0 < x b. /(x) = \ 0 < x

c. fix) = sinx —^ < x < ?f d. f(x) = e x —oo < x < oo

e. /(x) = -J?— -\<x<\ f. /(x) = 1 < x

J v 7 + 1 ~ ~ J w x 2 +1

g. /(x) = e t 0 < x h. f(x) = x\x\ — OO < X < oo

i. f{ x ) = x 3 – 6x 2 + 9x – 4 1 < x < 3

Exercise 12.2.2 Find the intervals on which / is increasing. Identify the local minima and local maxima. Plot the local minima and local maxima on a graph, and sketch a candidate graph of the function.

a. fix) = x 2 – 3x + 7 b. /(x) = -x 2 + 5x + 16

c. fix) = 3x 4 + 8x 3 – 6x 2 – 24x + 17 d. /(x) = x 5 – 5x + 2 e. fix) = x 4 + 4x + 8 f. fix) = xlnx

g. fix) = xe~ x h. fix) = x 2 e~ x

Exercise 12.2.3 Prove Theorem 12.2.2. The proof will be similar to that for Theorem 8.1.1 except that by hypothesis P\c) > 0 instead of -P'( c ) — 0> which leads to subsequent changes.

Exercise 12.2.4 Complete the argument for Case 1, of Theorem 12.2.3 by treating the event that c < x.

Exercise 12.2.5 Show that for the function

F(h) = (1 + h) 1/h F’ih) < 0 for 0 < h < 1.

Suggestion:

1 h 2 F’ih) h

Let In F(h) = – ln(l + h), and show that \ ; = –ln(l + /i).

h ^{h) 1 + h

Note that h 2 and F(h) are positive on 0 < h < 1, so that to show that F’ < 0 It is sufficient to show that

G(/iO = ^ – – – ln(l + /i) is negative on 0 < h < 1. Show that G(0) = 0 and < 0 and conclude that G{h) < 0 for 0 < h < 1.

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS 12.3 Approximating functions with quadratic polynomials.

520

Three Questions.

1. Pat is looking for Mike. Sean tells Pat that three minutes ago he saw Mike at the corner of First and Main. Where should Pat go to find Mike?

2. Pat is looking for Mike. Sean tells Pat that three minutes ago he saw Mike at the corner of First and Main and he was jogging North on Main at the rate of 2 blocks per minute. Where should Pat go to find Mike?

3. Pat is looking for Mike. Sean tells Pat that three minutes ago he saw Mike at the corner of First and Main and he was jogging North on Main at the rate of 2 blocks per minute, but Mike looked like he was getting tired. Where should Pat go to find Mike?

The first two questions above have reasonably defensible answers, and you likely worked them out as you read them.

1. If Pat only knows that Mike was at First and Main three minutes ago, it seems the best he could do is to go to First and Main and look for Mike.

2. If in addition, Pat knows that Mike was jogging North at 2 blocks per minute, Pat should look for Mike 6 blocks north of First and Main, which we will take to be Seventh and Main. This assumes that Mike’s jogging remains constant, and that he is not, for example, running laps around the court house at First and Main.

3. If it looked as if Mike was getting tired, we are not sure, but Mike might also be slowing down. Perhaps Pat should look for Mike at about Fifth or Sixth and Main. The question hinges on how rapidly Mike was slowing down as a result of being tired.

Of course there might be other useful information. For example, Mike might be eating a quick energy bar and regaining some of his strength!

To make the questions more specific we pose the following similar questions.

1. Suppose / is a function and /(0) = 1. Ten points of your next examination depends on your estimate of /(3). What is your best estimate?

2. Suppose / is a function and

/(0) = 1 and /’ (0) = 2

What is your best estimate of /(3)? (Another 10 points.)

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

521

3. Suppose / is a function and

/(0) = 1 and /'(())= 2 and /”(0) = ~

What is your best estimate of /(3)? (Good for 15 points.) (Note: The condition, /”(0) = — \ or just /”(0) is negative implies that f'(t) is decreasing (Pat is slowing down).)

Again the first two questions have fairly defensible answers, and we wish to develop a rational approach to the third question,

1. Knowing only that /(0) = 1 our best guess of /(3) is also 1. Without knowledge of how / may change in [0,3], our guess is that it does not change, and for all t between 0 and 3 our guess of f(t) is 1.

2. If we know that /(0) = 1 and /'(0) = 2, clearly the value of / is increasing, but we assume that f'(t) is unchanging from /'(0) (no reason to suppose that it is either higher or lower). If so, then the graph of / is a straight line, L{t), between 1 and 3 and

L(t) = 1 + 2 t so that L(3) = 1 + 2×3 = 7.

Note that the straight line fit) = 1 + 2t is perhaps the simplest function we can find for which /(0) = 1 and f(0) = 2.

3. Now suppose that

/(0) = 1 and /'(())= 2 and /”(0) = -\

We assume that f”(t) — — \ for all 0 < t < 3, and our strategy is to find the most simple function, /, with these properties. We choose polynomials as ‘simple’ and in particular look for a parabola,

P(t) = Po + Pit + P2t 2

with the stated properties. We need to decide what to choose for p 0 , p\ and p-i. In order to match the information about / we will insist that

p(0) = 1 and p'(0) = 2 and p”(0) = ~

It is easy, as the array in Table 12.1 shows. Thus we conclude that

P(t) = Po+Pit + p 2 t 2 = l + 2t~lt 2

o

has the required properties and is simple. Our guess is that

1 7

/(3) should be p(3) = 1 + 2- 3- – 3 2 = 5-

8 8

For future reference, note that

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

522

Table 12.1: Array for matching coefficients of quadratics. Analysis of pit) Value at 0 Required value Coefficient

P(t) =P0+Plt + P2t 2 p(t)\ t=0 =Po p(0) = 1 Po = 1

p'(t) = Pl + 2p 2 t p'(t)\ t=0 = Pl p'(0) = 2 Pl = 2

P”(t) = 2p 2 p”(t)\ t=0 = 2p 2 p”(0) = -l p 2 = -\

Exercises for Section 12.3, Approximating functions with quadratic polynomials.

Exercise 12.3.1 If you know that the temperature range was from a low of 60°F to a high of 84°F on Monday, what is your best estimate for the temperature range on Tuesday?

Exercise 12.3.2 Suppose you are measuring the growth of a corn plant, and observe that

a. The plant is 14 cm tall at 10:00 am Monday and 15.5 cm tall at 10:00 am on Tuesday. What is your best guess for the height of the plant at 10:00 am on Thursday?

b. The plant is 14 cm tall at 10:00 am on Monday, 15.5 cm tall at 10:00 am on Tuesday, and 17.5 cm tall at 10:00 am on Wednesday. What is your best guess for the height of the plant at 10:00 am on Thursday?

Exercise 12.3.3 In Table 12.1 we computed two derivatives, p’ and p”, that you should be sure you understand.

Find p'(t), p”(t) (the derivative of p’), p”‘(t) = p^ (the derivative of p”), p””(t) = p^ and p( 5 \t). In parts f – g it is easiest to retain the binomial form and use

g . p {t) = p(t) = 3 + 4(t-5)-2(t-5) 2 + |(t-5) 3 -|(t-5) 4

h. p(t) = po + piit – 3) + p 2 (t – 3) 2 + p 3 (t – 3) 3

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

523

12.4 Polynomial approximation anchored at 0.

The procedure we introduced in the previous section, Section 12.3, extends to polynomials of all degrees. It is remarkably accurate when used to approximate functions. We use it to find a cubic polynomial that approximates sinx close to the anchor point, a = 0. To do so, we let f(x) = sin a; and compute /(0), f'(0), f”(0), and f”‘(0). Then we seek a cubic polynomial

p(x) = po + pi x + p 2 x 2 + p 3 x 3

that matches these values, meaning that

P (o) = /(o) p'(o) = /'(o) p”(o) = r (o) p”‘(o) = r (o)

The information is organized in Table 12.2.

Table 12.2: Array to show the match of cubic coefficients. . Analysis of f(x) = sin(x) Analysis of p(x) = po + p\ x + p 2 x 2 + x 3

a = 0 a = 0

/(x)=sinx /(0)=sin0 = 0 p(x) = po + p\ x + p 2 x 2 + p% x 3 p(0) = po

f'(x) = cosx / / (0) = cos0 = l p'(x) = p\ + 2p 2 ^ + 3j>3x 2 p'(0) = pi /”(x) = -sinx /”(0) = -sinO = 0 p”(x) = 2p 2 + 3 • 2p 3 x p”(0) = 2p 2

f”(x) = – cos x /'”(0) = – cos 0 = -1 p'”(x) = 3 • 2p 3 p”‘(0) = 3 • 2 p 3

Match at a = 0, Po = 0, pi = 1, P2 = 0, p 3 = g4j

The match of derivatives in the last row of Table 12.2 is obtained by equating boldfaced entries in the rows above; 0,1, 0, and —1 are matched with the po, pi, 2 p 2 and 3 • 2 p 3 , respectively. We conclude that

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

524

p(x) = x — ^ is sa id to be the cubic polynomial that matches f(x) = sinx at the anchor point, a = 0.

To see how well p(x) = x — §^ approximates f(x) = sinx, the graphs of both are drawn in Figure 12.6, for — | < x < |. The graphs are indistinguishable on —| < £ < |. The values at | are

sin ^ = 0.7071 = 0.7047

4 v 4 y

so that

Absolute Error = |0.7047 – 0.70711 = 0.0024

(12.6)

Relative Error = ^ggf^ = 0-0034

‘ :: 7t/2 =i/4 6 i/4 i72″

Figure 12.6: Graphs of f(x) = sinx and p(x) = x — (dashed line), the cubic polynomial that matches the sine graph at the anchor point a = 0.

We can use more information about f(x) = sinx at a = 0 and find a quintic (fifth degree) polynomial that matches / at a = 0 and even more closely approximates /.

Let p(x) = po + Pi x + p 2 x 2 + p 3 x 3 + p 4 x A + p 5 x 5 and find p 0 , pi, p 2 , P3, Pa and p$ so that

P (o) = /(o) P ‘(o) = /’ (o) P “(o) = /” (o)

p (3) (o) = y (3) (Q) p (4) (0) = y (4) (Q) p (5) (o) = J(5) (Q)

We could use /'”, /””, and /”‘”, but this mode of counting is a bit primitive. It is useful to define

f {0) (t) = f(t) /«(*)=/'(f)

and f^(t) is the kth derivative of f(t).

f {2) (t) = f”(t)

Analysis of p(x)

p(x) = p 0 + pi x + p 2 x 2 + p 3 x 3 + p 4 x 4 + p 5 x 5 p(0) = po

p'(x) = pi + 2p 2 x + 3p 3 x 2 + 4p 4 x 3 + 5 J95X 4 p'(0) = pi

p”{x) = 2p 2 + 3-2p 3 x + 4-3p 4 x 2 + 5-4p 5 x 3 p”(0) = 2p 2

p( 3 )(x) = 3-2p 3 + 4-3-2p 4 x + 5-4-3p 5 x 2 p^{0) = 3-2p 3

p( 4 )( x ) =4-3-2p 4 + 5-4-3-2p 5 x p (4) (0) = 4 3-2p 4

Match: p( k )(0) = f( k )(0) Po = 0

Pi = 1

P2 = 0 P3 = ~

Pa = 0

p(V(x) = 5-4-3-2j9 5

p(5)(Q) = 5-4-3-2p 5 p 5

i_

5!

Observe that p 0 — 0, pi — 1, p 2 — 0 and p 3 = — ^ are the same as for the cubic approximation to the sin a;. The new terms are p 4 = 0 and p 5 = ^. Our quintic polynomial approximation to sin a; is

p(x) = x —

3 5

X X

3l + 5f

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS which is the previous cubic polynomial plus two terms, one of which is zero.

p(x) — x — |y + |j- is said to be the fifth degree polynomial that matches f(x) = sin a; at a = 0.

Exercises for Section 12.4, Polynomial approximation anchored at 0. Exercise 12.4.1 Draw the graphs of

f(x) = sinx and p(x) = x – — + — for – 7— < x < 7—

The graphs should be indistinguishable on — f < x < f.

The largest separation on — f < x < f occurs at x — f (and x = — |). Compute /(f), p(f), and the relative error in the approximation /(f) = p(f).

Exercise 12.4.2 Find a cubic polynomial, p(x) = po + Pi x + P2 x 2 + p^ x 3 that matches f(x) = at a = 0. To do so, you should complete the following table.

Analysis of f(x) = e x Analysis of p(x) Match: p( k )(0) = f( k )(0)

f(x) = e x /(0) = e° = 1 p(x) = po +Pi ^ + P2 x 2 + p s x 3 p(0) = po Po = 0

f'(x)=e x f(0) = e° = _ p'(s) =pi +2p 2 x + 3p 3 a; 2 j/(0) = Pi Pi =—

r(x)=_ no)=_=_ p”(x)= p”(o)=_ p 2 =—

/( 3 )(x)=_ /( 3 )(0)=_ = _ p( 3 )(x)= p( 3 )(0)=_ p 3 = —

You should conclude from the table that

9 3

p(x) = 1 + x + — + —

is the cubic polynomial that matches f(x) = e x at a = 0.

Draw the graphs of f(x) = e x and p(x) = 1 + x + a; 2 /2 + a; 3 /6 on — 1 < x < 1.

You should find a pretty good match. The maximum separation occurs at x — 1 with a maximum

II+ 1 + 1/2 +1/6-e 1 ! 12.6666 — 2.718281 Relative error = l – ‘— ‘- l – = l – l – = 0.02

e 1 e 1

There is about a 2% relative error at x — 1.

Compute the relative error in the approximation, e _1 = p(—1).

Exercise 12.4.3 Find a fourth degree polynomial, p(x) = po + Pi x + P2 x 2 + ps x 3 + p 4 x 4 , that matches f(x) = e x at the anchor point, a = 0. You did most of the work in the previous exercise Compute the relative errors in the approximations, e 1 = p(l) and e _1 = p{— 1).

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

527

Exercise 12.4.4 Find the quadratic polynomial, p(x) = po + p±x + P2X 2 , that matches fix) = cosx at the anchor point, a = 0. Draw the graphs of /(x) and p(x) and discuss the accuracy of the approximation, cos(|) = p(f).

Exercise 12.4.5 Find the fourth degree polynomial, p(x) = po + pi x + P2 x 2 + p^ x 3 + £>4 x 4 , that matches /(x) = cosx at the anchor point, a = 0. Draw the graphs of f(x) and p(x) and discuss the accuracy of the approximation, cos(|) = p(f )•

Exercise 12.4.6 Find a cubic polynomial, p(x) = p 0 + pi x + p 2 x 2 + p 3 x 3 that matches /(x) = e~ x at a = 0.

Exercise 12.4.7 Assume that the sixth degree polynomials, S(x), C(x), and E(x) that match, respectively, sin a;, cosx, and e x , are

S{x) = x-C{x) = 1-

z,: u:

a. Compute S”(x) and compare it with C(x).

b. Compute C'(x) and compare it with S(x).

c. Compute -E”(x) and compare it with E(x).

d. (Only for the adventurous.) Let i = Note that i 2 = —1, i 3 = i 2 ■ i = —i, and i A = i 2 ■ i 2 = 1, and continue this sequence. Compute E{i ■ x) and write it in terms of S(x) and C(x).

12.5 Polynomial approximations to solutions of differential equations.

You can find polynomials that approximate solutions to differential equations and we illustrate this for some simple equations for which you either already know or soon will know exact solutions.

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

528

Example 12.5.1 Problem: Find a polynomial, pit) = p 0 + p\ t + p 2 1 2 + p 3 t 3 + p A t 4 that approximates the solution to

y'(t)=y(t), 2/(0) = 1.

Solution: We need to find po, p±, p 2 , p 3 , and p^. We will insist that ‘p(t) matches y(t) at t — 0’ meaning that

p(0) = i/(0), p'(0) = y'(0), p< 2 >(0) = 2/ (2) (0), p( 3 )(0) = 2/ (3) (0) and p( 4 )(0) = 2/ (4) (0), Because

p(0)=po, p'(0)=Pi, p”(0) = 2p 2 , p^(0) = 3 • 2p 3 , and p (4) (0) =4-3-2-p 4 , it is sufficient to find values for

2/(0), y'(0), 2/ {2) (0), 2/ (3) (0), and 2/ (4) (0)-

We are given 2/(0) = 1.

Because y'(t)=y(t), y'(0) = y(0) = 1. Because y'(i) = y(*), 2/ (2) W = ?/'(*), and y^(0) = y'(0) = 1. Continuing we get

^(t) = y'(*) 1/ {3) W = 1/ (2) W y (3) (0) = 2/ (2) (0) = l

(f) = y^it) y W(t) = 2/ (3) W 2/ (4) (0) = 2/ (3) (0) = 1

By insisting that

p(0) = !/(0), p'(0)=y'(0), p( 2 )(0)=2/ (2) (0), ^(0) = 2/ {3) (0) and p^(0) = y^(0), we conclude that

1 1,1

Po = 1, pi = 1, p 2 = g» P3 = T^y, and p 4 = —,

and that

p(t) = l + t+V + ^ 3 + ^ 4 .

You know from Chapter 5 that y = e l solves y'(i) = y(t), y(0) = 1. The polynomial that we have found is the polynomial approximation to e* that you (may have) found in Exercise 12.4.3. Furthermore, we are usually interested in

y'(t) = ky(t), 2/(0) =j/o or y'(t) = -ky(t) y(0) = y 0

for which the solution is

y(t) = y 0 e kt or y(t) = y 0 e~ kt

In the first case

P(t) = p(kt) = 1 + kt + l -{ktf + ^{ktf + i(H) 4 approximates the solution and in the second case

Pit) = p(-kt) = 1 – kt + \{ktf – i(fct) 3 + i(H) 4 approximates the solution, h

Example 12.5.2 Problem: Find a polynomial, pit) = Po + pt + P2t 2 + p 3 t 3 + p 4 t 4 that approximates the solution to

y”(t) + y(t) = 0, y(0) = l, y'(0) = 0. (12.7)

Solution: We need to find po, p±, P2, P3, and p 4 . We will insist that ‘p(t) match at t — 0’ meaning that

p(0) = i/(0), p'(0) = j/(0), ^(0) = ^^(0), p^(0) = / 3 \0) and p<*>(0) = y (4) (0), Because

p(0)=Po, p'(0)=Pi, p”(0) = 2p 2 , p( 3 )(0) =3-2p 3 , and p^(0) = 4 • 3 • 2p 4 , it is sufficient to find values for

1/(0), y'(0), t/ 2 )(0), j/ 3 )(0), and j/ 4 )(0). We are given y(0) = 1 and y'(0) = 0.

Because t/ {2) (t) + y(t) = 0, y (2) (t) = -y(t), and y (2) (0) = -y(0) = -1. Furthermore,

j,(3)( t ) = y (3) (0) = _^( 0 )=0

yW(t) = -yP)(t) yW(0) = -y( 2 )(0) = l

By matching p(t) to y(t) at t = 0 we get

Po = 1, Pi = 0, p 2 = -1/2, p 3 = 0, and p 4 = -1/4!

so that

The solution to Equation 12.7 is y = cost and pit) is a close approximation to y(t) on the interval [-7r/2,7r/2]. For

y”(t)+u 2 y(t) = 0, 2/(0) = 1, j/(0) = 0, the solution is y(t) = cos cut and is approximated by

P(«)=p( U i) = l-^ + ^. –

Example 12.5.3 If your stomach turns queazy when dissecting a frog, you should skip this example.

Problem: Find a polynomial, pit) = Po + Pit + p 2 t 2 + p 3 t 3 + p 4 t 4 + p 5 ,t 5 that approximates the solution to the logistic equation

y'(t)=y(t)(l-y(t)), 2/(0) = 1/2. (12.8)

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

530

Solution: As in Examples 12.5.1 and 12.5.2 we will match derivatives at t — 0 to find the coefficients of p.

y'(t) y {2) (t)

,(3)

V

y

(4)

,(5)

By insisting that

we get

y(t)-y 2 (t)

y/(t)-2y(t)y'(t)

y m -2yy^ -2y’yW – Ay’y^

y

(3)_ 6

y y

(2)

%yy

(3)

y (4) _ 6 y / y (3) _ 6 ( y (2))2 _ 2 y y (4) _ 2 y > y (3)

yW(0)

p(*)

fc!

1 1

– + -t

2 4

A; = 0,1, 2, • • •, 5

1 o 1 5 t -\ t 5

48 480

1/(0) = | 2/ (2) (0) = 0

z/ (3) (o) = – J

2/ (4) (0) = 0 Z/ (5) (0) = \

The actual solution to Equation 12.8 is y(t) = e*/(l + e*) and graphs of y and p are shown in Figure 12.5.3.3. Equation 12.8 is an equation for logistic growth with the initial population size equal to one-half the maximum supportable population (equal to 1), and (0,1/2) is an inflection point of the curve. Polynomials do not have horizontal asymptotes and must eventually increase without bound or decrease without bound, m

Figure for Example 12.5.3.3 Graphs of y(t) = e*/(l + e*) and p(t) = \ + \ t ~

!*3

r + 48TJ t •

Time

Exercises for Section 12.5, Polynomial approximation to solutions of differential

equations.

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

531

Exercise 12.5.1 Find polynomials of degree specified that approximate solutions to the equations shown.

Degree

Exercise 12.5.2 Suppose y(t) solves

y’ = k y(t) (1 – y(t)) and z(t) = M y(kt).

Show that z(t) solves

z(ty

z'(t) = kz(t) (l –

M

12.6 Polynomial approximation at anchor a ^ 0.

All of the polynomials approximations we have found so far have matched data at the anchor point, a = 0. If we wish to find a polynomial approximation to f(x) = In re, because InO is not defined, we will have to choose an anchor point other than a = 0. We can choose a = 1 as our anchor point, and as before, look for p(x) = po + Vi x + P2X 2 that matches f(x) = In x at the anchor point, a = 1, as follows.

Analysis of / Analysis of p(x) = po + p\ x + P2 x 2 Match

p(k)(i) = f (k)( 1 )

f(x) = lnx /(l)=lnl = 0 p(x) = po + p! x + p 2 x 2 = Po + Pi + P2 Po + Pi + Vi = 0

f[x) = \ /'(1) = I = 1 p'(x)=p 1+ 2p 2 x p'(l) = Pl + 2p 2 Pl +2p 2 = l

f”(x) = £ /»(l) = -£ = -l p”{x) = 2p 2 P”(l) = 2p 2 2p2 = -l

Now we solve a system of equations (from bottom to top), Po + Pi + P2 = 0

Pi+2p 2 = 1 y , i + 2.(-i) = I p , = 2

2p 2 = -1

They are easy to solve, from the ‘bottom up’. That is, find p 2 = —\ from the last equation. Substitute — \ for p 2 in the second equation and compute p\ = 2. Then use these two values in the

first equation to solve pi = 3

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

532

Now our quadratic polynomial is

p(x) = — + 2x- l -x 2 (12.9)

and it can be seen in Figure 12.7 that it gives a fair fit on the interval — \ < x < |.

Without showing the arithmetic, we claim that the cubic that matches f(x) = Inx at the anchor a = 1 is

(12.10)

_ 2 i—i 1 1 1 1 1 1 1 1 1—i

0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

Figure 12.7: Graphs of f(x) = Inx and p(x) = — | + 2x — \x 2 . (dashed line), the quadratic polynomial that matches the natural logarithm graph at the anchor point a = 1.

Observe that the terms of the cubic in Equation 12.10 have no obvious relation to the terms of the quadratic in Equation 12.9, contrary to our experience when the anchor point was a = 0. When the anchor of the data is a = 1, the polynomial form

p(x) = 7T 0 + TTi (X – 1) + 7T 2 (x – l) 2

is preferred for two reasons. First equations for the coefficients each involve only one unknown coefficient and are very easy to solve. More importantly, after a quadratic approximation has been obtained, if later we wish to compute a cubic approximation, its first three terms are the terms of the quadratic and we only have to compute one new coefficient. We illustrate this idea. Compute 7r 0 , 7ri, and 7r 2 so that the quadratic

p(x) = 7T 0 + TTi (X – 1) + 7T 2 (x – l) 2

matches f(x) = Inx at the anchor point, a = 1. Analysis of f(x) = Inx f(x) = \nx /(l) = lnl = 0 fix) = A /'(l) = i = 1

Analysis of p(x) = n 0 + 7Ti(x — 1) + 7r 2 (x — l) 2 Match

pW(l) = fW(l)

p(x) = 7T 0 + 7Ti (x – 1) + 7T 2 (x – l) 2 = 7T 0 7T 0 = 0

p'(x) = 7Ti + 2 7T 2 (X – 1) = 7Ti 7Ti = 1

p( 2 )(x)=2 7T 2 P ( 2 )(1) = 27T 2 7T2 = -|

Then

p(x) = 0 + 1 • (x – 1) – 1 • (x – l) 2

2

is the quadratic polynomial that matches /(x) = lnx at the anchor point, a — 1. This is the same quadratic polynomial as first computed. We expand (x — l) 2 and collect terms.

p(x) = ( x – 1) – *(x – l) 2

= x – 1 – ^(x 2 – 2x + 1)

1 2 1

= +x–

3 o 1 2

= -2 +2x -2 X

which is the earlier quadratic form.

It is relatively easy now to compute a cubic

p(x) = 7T 0 + 7Ti(x – 1) + 7T 2 (X – l) 2 + 7T 3 (x – l) 3

that matches /(x) = lnx at the anchor point, a = 1. Analysis of /(x) = lnx /(x) = lnx /(l)=lnl = 0

/'(*) = I /'(I) = 1 = 1

Z (2) (*) = -^ /^(i) = -^ = -i

/ (3) (*) = ^ / (3) (l) = ^ = l

CHAPTER 12. THE MEAN VALUE THEOREM; TAYLOR POLYNOMIALS

Analysis of p(x) = n 0 + 7Ti (x — 1) + 7r 2 (x — l) 2 + n 3 (x — l) 3 Match