In the following exercises, use the limit laws to evaluate each limit. Justify each step by indicating the appropriate limit law(s).
83) \(\displaystyle \lim_{x→0}(4x^2−2x+3)\)
- Answer:
-
Use constant multiple law and difference law:
\(\displaystyle \lim_{x→0}(4x^2−2x+3)=4 \displaystyle \lim_{x→0}x^2−2 \displaystyle \lim{x→0}x+ \displaystyle \lim_{x→0}3=3\)
84) \(\displaystyle \lim_{x→1}\frac{x^3+3x^2+5}{4−7x}\)
85) \(\displaystyle \lim_{x→−2}\sqrt{x^2−6x+3}\)
- Answer:
-
Use root law: \(\displaystyle \lim_{x→−2}\sqrt{x^2−6x+3}=\sqrt{ \displaystyle \lim_{x→−2}(x2−6x+3)}=\sqrt{19}\)
86) \(\displaystyle \lim_{x→−1}(9x+1)^2\)
In the following exercises, use direct substitution to evaluate each limit.
87) \(\displaystyle \lim_{x→7}x^2\)
- Answer:
- 49
88) \(\displaystyle \lim_{x→−2}(4x^2−1)\)
89) \(\displaystyle \lim_{x→0}\frac{1}{1+\sin x}\)
- Answer:
- 1
90) \(\displaystyle \lim_{x→2}e^{2x−x^2}\)
91) \(\displaystyle \lim_{x→1}\frac{2−7x}{x+6}\)
- Answer:
- \(−\frac{5}{7}\)
92) \(\displaystyle \lim_{x→3}\ln e^{3x}\)
In the following exercises, use direct substitution to show that each limit leads to the indeterminate form \(0/0\). Then, evaluate the limit.
93) \(\displaystyle \lim_{x→4}\frac{x^2−16}{x−4}\)
- Answer:
- \(\displaystyle \lim_{x→4}\frac{x^2−16}{x−4}=\frac{16−16}{4−4}=\frac{0}{0}; then, \displaystyle \lim_{x→4}\frac{x^2−16}{x−4}= \displaystyle \lim_{x→4}\frac{(x+4)(x−4)}{x−4}=8\)
94) \(\displaystyle \lim_{x→2}\frac{x−2}{x^2−2x}\)
95) \(\displaystyle \lim_{x→6}\frac{3x−18}{2x−12}\)
- Answer:
- \( \displaystyle \lim_{x→6}\frac{3x−18}{2x−12}=\frac{18−18}{12−12}=\frac{0}{0}\)
then, \(\displaystyle \lim_{x→6}\frac{3x−18}{2x− 12}=\displaystyle \lim_{x→6}\frac{3(x−6)}{2(x−6)}=\frac{3}{2}\)
96) \(\displaystyle \lim_{h→0}\frac{(1+h)^2−1}{h}\)
97) \( \displaystyle \lim _{t→9}\frac{t−9}{\sqrt{t}−3}\)
- Answer:
- \(\displaystyle \lim_{x→9}\frac{t−9}{\sqrt{t}−3}=\frac{9−9}{3−3}=\frac{0}{0}; then, \displaystyle \lim_{t→9}\frac{t−9}{\sqrt{t}−3} =\displaystyle \lim_{t→9}\frac{t−9}{\sqrt{t}−3}\frac{\sqrt{t}+3}{\sqrt{t}+3}=\displaystyle \lim_{t→9}(\sqrt{t}+3)=6\)
98) \(\displaystyle \lim_{h→0}\frac{\frac{1}{a+h}−\frac{1}{a}}{h}\), where a is a real-valued constant
99) \(\displaystyle \lim_{θ→π}\frac{\sin θ}{\tan θ}\)
- Answer:
- \(\displaystyle \lim_{θ→π}\frac{\sin θ}{\tan θ}=\frac{\sin π}{\tan π}=\frac{0}{0}; then, \displaystyle \lim_{θ→π}\frac{\sin θ}{\tan θ}=\displaystyle \lim_{θ→ π}\frac{\sin θ}{\frac{\sin θ}{\cos θ}}=\displaystyle \lim_{θ→π}\cos θ=−1\)
100) \(\displaystyle \lim_{x→1}\frac{x^3−1}{x^2−1}\)
101) \(\displaystyle \lim_{x→1/2}\frac{2x^2+3x−2}{2x−1}\)
- Answer:
- \(\displaystyle \lim_{x→1/2}\frac{2x^2+3x−2}{2x−1}=\frac{\frac{1}{2}+\frac{3}{2}−2}{1−1}=\frac{0}{0}; then, \displaystyle \lim_{x→ 1/2}\frac{2x^2+3x−2}{2x−1}=\displaystyle \lim_{x→1/2}frac{(2x−1)(x+2)}{2x−1}=\frac{5}{2}\)
102) \(\displaystyle \lim_{x→−3}\frac{\sqrt{x+4}−1}{x+3}\)
In the following exercises, use direct substitution to obtain an undefined expression. Then, use the method of Example to simplify the function to help determine the limit.
103) \(\displaystyle \lim_{x→−2^−}\frac{2x^2+7x−4}{x^2+x−2}\)
- Answer:
- −∞
104) \( \displaystyle \lim _{x→−2^+}\frac{2x^2+7x−4}{x^2+x−2}\)
105) \( \displaystyle \lim _{x→1^−}\frac{2x^2+7x−4}{x^2+x−2}\)
- Answer:
- −∞
106) \(\displaystyle \lim_{x→1^+}\frac{2x^2+7x−4}{x^2+x−2}\)
In the following exercises, assume that \(\displaystyle \lim_{x→6}f(x)=4,\displaystyle \lim_{x→6}g(x)=9\), and \(\displaystyle \lim_{x→6}h(x)=6\). Use these three facts and the limit laws to evaluate each limit
107) \(\displaystyle \lim_{x→6}2f(x)g(x)\)
- Answer:
- \(\displaystyle \lim_{x→6}2f(x)g(x)=2\displaystyle \lim_{x→6}f(x)\displaystyle \lim_{x→6}g(x)=72\)
108) \(\displaystyle \lim_{x→6}\frac{g(x)−1}{f(x)}\)
109) \(\displaystyle \lim_{x→6}(f(x)+\frac{1}{3}g(x))\)
- Answer:
- \(\displaystyle \lim_{x→6}(f(x)+\frac{1}{3}g(x))=\displaystyle \lim_{x→6}f(x)+\frac{1}{3}\displaystyle \lim_{x→6}g(x)=7\)\
110) \(\displaystyle \lim_{x→6}\frac{(h(x))^3}{2}\)
111) \(\displaystyle \lim_{x→6}\sqrt{g(x)−f(x)}\)
- Answer:
- \(\displaystyle \lim_{x→6}\sqrt{g(x)−f(x)}=\sqrt{\displaystyle \lim_{x→6}g(x)−\displaystyle \lim_{x→6}f(x)}=\sqrt{5}\)
112) \(\displaystyle \lim_{x→6}x⋅h(x)\)
113) \(\displaystyle \lim_{x→6}[(x+1)⋅f(x)]\)
- Answer:
- \(\displaystyle \lim_{x→6}[(x+1)f(x)]=(\displaystyle \lim_{x→6}(x+1))(\displaystyle \lim_{x→6}f(x))=28\)
114) \(\displaystyle \lim_{x→6}(f(x)⋅g(x)−h(x))\)
[T] In the following exercises, use the definition of the piecewise-defined function to evaluate the given limits (you may want to draw the graph).
115) \(f(x)=\begin{cases}x^2 & x≤3,\\ x+4 & x>3\end{cases}\)
- a. \(\displaystyle \lim_{x→3^−}f(x)\)
- b. \(\displaystyle \lim_{x→3^+}f(x)\)
- c. \(\displaystyle \lim_{x→3}f(x)\)
- Answer:
-
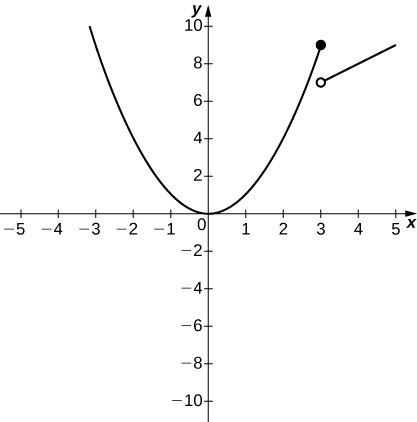
a. 9; b. 7; c. DNE
.
116) \(g(x)=\begin{cases}x^3−1 & x≤0\\1 & x>0\end{cases}\)
- a. \(\displaystyle \lim_{x→0^−}g(x)\)
- b. \(\displaystyle \lim_{x→0^+}g(x)\)
- c. \(\displaystyle \lim_{x→0}g(x)\)
117) \(h(x)=\begin{cases}x^2−2x+1 & x<2\\3−x & x≥2\end{cases}\)
- a. \(\displaystyle \lim_{x→2^−}h(x)\)
- b. \(\displaystyle \lim_{x→2^+}h(x)\)
- c. \(\displaystyle \lim_{x→2}h(x)\)
- Answer:
- a. 1; b. 1; c. 1
In the following exercises, use the following graphs and the limit laws to evaluate each limit.
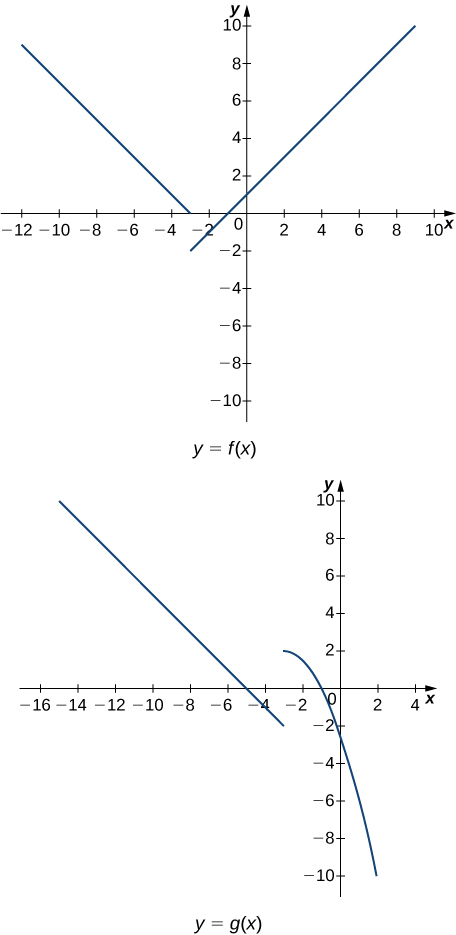
118) \(\displaystyle \lim_{x→−3^+}(f(x)+g(x))\)
119) \(\displaystyle \lim_{x→−3^−}(f(x)−3g(x))\)
- Answer:
- \(\displaystyle \lim_{x→−3^−}(f(x)−3g(x))=\displaystyle \lim_{x→−3^−}f(x)−3\displaystyle \lim_{x→−3^−}g(x)=0+6=6\)
120) \(\displaystyle \lim_{x→0}\frac{f(x)g(x)}{3}\)
121) \(\displaystyle \lim_{x→−5}\frac{2+g(x)}{f(x)}\)
- Answer:
- \(\displaystyle \lim_{x→−5}\frac{2+g(x)}{f(x)}=\frac{2+(\displaystyle \lim_{x→−5}g(x))}{\displaystyle \lim_{x→−5}f(x)}=\frac{2+0}{2}=1\)
122) \(\displaystyle \lim_{x→1}(f(x))^2\)
123) \(\displaystyle \lim_{x→1}\sqrt{f(x)−g(x)}\)
- Answer:
- \(\displaystyle \lim_{x→1}\sqrt[3]{f(x)−g(x)}=\sqrt[3]{\displaystyle \lim_{x→1}f(x)−\displaystyle \lim_{x→1}g(x)}=\sqrt[3]{2+5}=\sqrt[3]{7}\)
124) \(\displaystyle \lim_{x→−7}(x⋅g(x))\)
125) \(\displaystyle \lim_{x→−9}[x⋅f(x)+2⋅g(x)]\)
- Answer:
- \( \displaystyle \lim _{x→−9}(xf(x)+2g(x))=( \displaystyle \lim _{x→−9}x)( \displaystyle \lim _{x→−9}f(x))+2 \displaystyle \lim _{x→−9}(g(x))=(−9)(6)+2(4)=−46\)
For the following problems, evaluate the limit using the squeeze theorem. Use a calculator to graph the functions \(f(x),g(x)\), and \(h(x)\) when possible.
126) [T] True or False? If \(2x−1≤g(x)≤x^2−2x+3\), then \( \displaystyle \lim _{x→2}g(x)=0\).
127) [T] \( \displaystyle \lim _{θ→0}θ^2\cos(\frac{1}{θ})\)
- Answer:
-
The limit is zero.
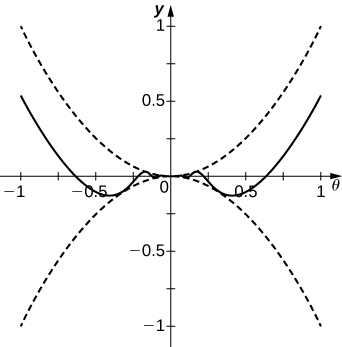
128) \( \displaystyle \lim _{x→0}f(x)\), where \(f(x)=\begin{cases}0 & x rational\\ x^2 & x irrrational\end{cases}\)
129) [T] In physics, the magnitude of an electric field generated by a point charge at a distance r in vacuum is governed by Coulomb’s law: \(E(r)=\frac{q}{4πε0_r^2}\), where E represents the magnitude of the electric field, q is the charge of the particle, r is the distance between the particle and where the strength of the field is measured, and \frac{1}{4πε_0} is Coulomb’s constant: \(8.988×109\,\text{N⋅m}^2/\text{C}^2\).
a. Use a graphing calculator to graph \(E(r)\) given that the charge of the particle is \(q=10^{−10}\).
b. Evaluate \( \displaystyle \lim _{r→0^+}E(r)\). What is the physical meaning of this quantity? Is it physically relevant? Why are you evaluating from the right?
- Answer:
-
a
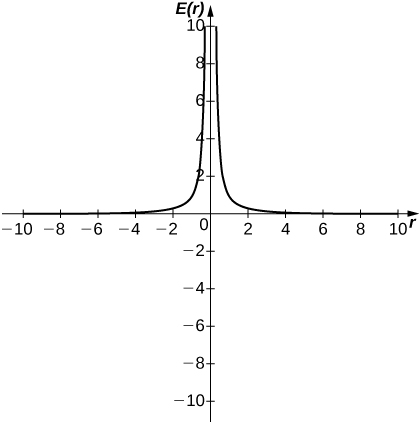
b. ∞. The magnitude of the electric field as you approach the particle q becomes infinite. It does not make physical sense to evaluate negative distance.
130) [T] The density of an object is given by its mass divided by its volume: \(ρ=m/V.\)
a. Use a calculator to plot the volume as a function of density \((V=m/ρ)\), assuming you are examining something of mass 8 kg (\(m=8\)).
b. Evaluate \( \displaystyle \lim _{x→0^+}V(\rho)\) and explain the physical meaning.
Chapter Review Exercises
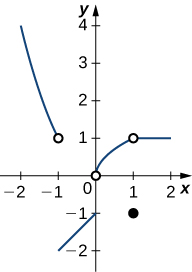
212) Using the graph, find each limit or explain why the limit does not exist.
a. \(\displaystyle \lim_{x→−1}f(x)\)
b. \(\displaystyle \lim_{x→1}f(x)\)
c. \(\displaystyle \lim_{x→0^+}f(x)\)
d. \(\displaystyle \lim_{x→2}f(x)\)
In the following exercises, evaluate the limit algebraically or explain why the limit does not exist.
213) \(\displaystyle \lim_{x→2}\frac{2x^2−3x−2}{x−2}\)
- Answer:
- 5
214) \(\displaystyle \lim_{x→0}3x^2−2x+4\)
215) \(\displaystyle \lim_{x→3}\frac{x^3−2x^2−1}{3x−2}\)
- Answer:
- 8/7
216) \(\displaystyle \lim_{x→π/2}\frac{cotx}{cosx}\) This is covered in section 2.4
217) \(\displaystyle \lim_{x→−5}\frac{x^2+25}{x+5}\)
- Answer:
- DNE
218) \(\displaystyle \lim_{x→2}\frac{3x^2−2x−8}{x^2−4}\)
219) \(\displaystyle \lim_{x→1}\frac{x^2−1}{x^3−1}\)
- Answer:
- 2/3
220) \(\displaystyle \lim_{x→1}\frac{x^2−1}{\sqrt{x}−1}\)
221) \\displaystyle \(lim_{x→4}\frac{4−x}{\sqrt{x}−2}\)
- Answer:
- −4
222) \(\displaystyle \lim_{x→4}\frac{1}{\sqrt{x}−2}\)
In the following exercises, use the squeeze theorem to prove the limit.
223) \(\displaystyle \lim_{x→0}x^2cos(2πx)=0\)
- Answer:
- Since \(−1≤cos(2πx)≤1\), then \(−x^2≤x^2cos(2πx)≤x^2\). Since \(lim_{x→0}x^2=0=lim_{x→0}−x^2\), it follows that \(lim_{x→0}x^2cos(2πx)=0\).
224) \(\displaystyle \lim_{x→0}x^3sin(\frac{π}{x})=0\)






