2.5E: Limits at Infinity EXERCISES

Last updated
Save as PDF

Page ID: 20573

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

2.5E: Limits at Infinity EXERCISES

For the following exercises, examine the graphs. Identify where the vertical asymptotes are located.

251)

Answer:: $x=1$

252)

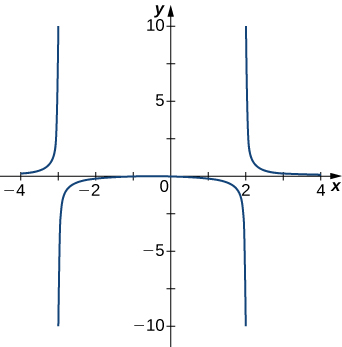
$CNX_Calc_Figure_04_06_202.jpeg$

253)

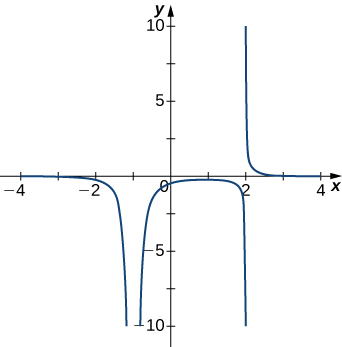
$CNX_Calc_Figure_04_06_203.jpeg$

Answer:: $x=−1,x=2$

254)

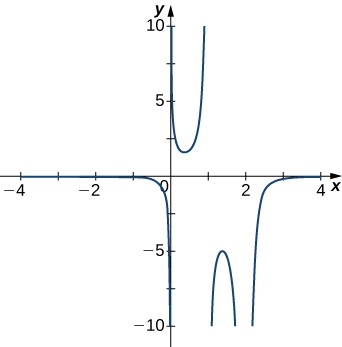
$CNX_Calc_Figure_04_06_204.jpeg$

255)

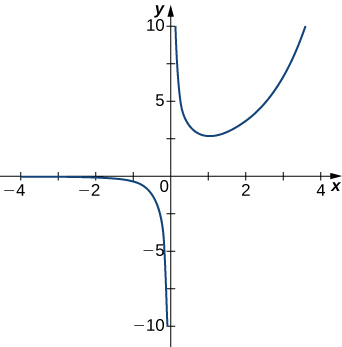
$CNX_Calc_Figure_04_06_205.jpeg$

Answer:: $x=0$

For the following functions $f(x)$, determine whether there is an asymptote at $x=a$. Justify your answer without graphing on a calculator.

256) $f(x)=\frac{x+1}{x^2+5x+4},a=−1$

257) $f(x)=\frac{x}{x−2},a=2$

Answer:: Yes, there is a vertical asymptote

258) $f(x)=(x+2)^{3/2},a=−2$

259) $f(x)=(x−1)^{−1/3},a=1$

Answer:: Yes, there is vertical asymptote

260) $f(x)=1+x^{−2/5},a=1$

For the following exercises, evaluate the limit.

261) $\displaystyle \lim_{x→∞}\frac{1}{3x+6}$

Answer:: $0$

262) $\displaystyle \lim_{x→∞}\frac{2x−5}{4x}$

263) $\displaystyle \lim_{x→∞}\frac{x^2−2x+5}{x+2}$

Answer:: $∞$

264) $\displaystyle \lim_{x→−∞}\frac{3x^3−2x}{x^2+2x+8}$

265) $\displaystyle \lim_{x→−∞}\frac{x^4−4x^3+1}{2−2x^2−7x^4}$

Answer:: $−\frac{1}{7}$

266) $\displaystyle \lim_{x→∞}\frac{3x}{\sqrt{x^2+1}}$

267) $\displaystyle \lim_{x→−∞}\frac{\sqrt{4x^2−1}}{x+2}$

Answer:: $−2$

268) $\displaystyle \lim_{x→∞}\frac{4x}{\sqrt{x^2−1}}$

269) $\displaystyle \lim_{x→−∞}\frac{4x}{\sqrt{x^2−1}}$

Answer:: $−4$

270) $\displaystyle \lim_{x→∞}\frac{2\sqrt{x}}{x−\sqrt{x}+1}$

For the following exercises, find the horizontal and vertical asymptotes.

271) $f(x)=x−\frac{9}{x}$

Answer:: Horizontal: none, vertical: $x=0$

272) $f(x)=\frac{1}{1−x^2}$

273) $f(x)=\frac{x^3}{4−x^2}$

Answer:: Horizontal: none, vertical: $x=±2$

274) $f(x)=\frac{x^2+3}{x^2+1}$

275) $f(x)=sin(x)sin(2x)$

Answer:: Horizontal: none, vertical: none

276) $f(x)=cosx+cos(3x)+cos(5x)$

277) $f(x)=\frac{xsin(x)}{x^2−1}$

Answer:: Horizontal: $y=0,$ vertical: $x=±1$

278) $f(x)=\frac{x}{sin(x)}$

279) $f(x)=\frac{1}{x^3+x^2}$

Answer:: Horizontal: $y=0,$ vertical: $x=0$ and $x=−1$

280) $f(x)=\frac{1}{x−1}−2x$

281) $f(x)=\frac{x^3+1}{x^3−1}$

Answer:: Horizontal: $y=1,$ vertical: $x=1$

282) $f(x)=\frac{sinx+cosx}{sinx−cosx}$

283) $f(x)=x−sinx$

Answer:: Horizontal: none, vertical: none

284) $f(x)=\frac{1}{x}−\sqrt{x}$

For the following exercises, construct a function $f(x)$ that has the given asymptotes.

285) $x=1$ and $y=2$

Answer:: Answers will vary, for example: $y=\frac{2x}{x−1}$

286) $x=1$ and $y=0$

287) $y=4, x=−1$

Answer:: Answers will vary, for example: $y=\frac{4x}{x+1}$

288) $x=0$

CHAPTER REVIEW EXERCISES

CR 1) $\displaystyle \lim_{x→∞}\frac{3x\sqrt{x^2+1}}{\sqrt{x^4−1}}$

Answer:: $3$

CR 2) $\displaystyle \lim_{x→∞}cos(\frac{1}{x})$

CR 3) $\displaystyle \lim_{x→1}\frac{x−1}{sin(πx)}$

Answer:: $−\frac{1}{π}$

CR 4) $\displaystyle \lim_{x→∞}(3x)^{1/x}$