8.4: Integration of Elementary Functions

In Chapter 5, integration was treated as antidifferentiation. Now we adopt another, measure-theoretical approach.

Lebesgue's original theory was based on Lebesgue measure (Chapter 7, §8). The more general modern treatment develops the integral for functions $f : S \rightarrow E$ in an arbitrary measure space. Henceforth, $(S, \mathcal{M}, m)$ is fixed, and the range space $E$ is $E^{1}, E^{*}, C, E^{n},$ or another complete normed space. Recall that in such a space, $\sum_{i}\left|a_{i}\right|<\infty$ implies that $\sum a_{i}$ converges and is permutable (Chapter 7, §2).

We start with elementary maps, including simple maps as a special case.

Definition

Let $f : S \rightarrow E$ be elementary on $A \in \mathcal{M};$ so $f=a_{i}$ on $A_{i}$ for some $\mathcal{M}$-partition

$$A=\bigcup_{i} A_{i} \text { (disjoint).}$$

(Note that there may be many such partitions.)

We say that $f$ is integrable (with respect to $m$), or $m$-integrable, on $A$ iff

$$\sum\left|a_{i}\right| m A_{i}<\infty.$$

(The notation "$|a_{i}| m A_{i}$" always makes sense by our conventions (2*) in Chapter 4, §4.) If $m$ is Lebesgue measure, then we say that $f$ is Lebesgue integrable, or L-integrable.

We then define $\int_{A} f,$ the $m$-integral of $f$ on $A,$ by

$$\int_{A} f=\int_{A} f d m=\sum_{i} a_{i} m A_{i}.$$

(The notation "$dm$" is used to specify the measure $m$.)

The "classical" notation for $\int_{A} f d m$ is $\int_{A} f(x) d m(x)$.

Note 1. The assumption

$$\sum\left|a_{i}\right| m A_{i}<\infty$$

implies

$$(\forall i) \quad\left|a_{i}\right| m A_{i}<\infty;$$

so $a_{i}=0$ if $m A_{i}=\infty,$ and $m A_{i}=0$ if $|a_{i}|=\infty.$ Thus by our conventions, all "bad" terms $a_{i} m A_{i}$ vanish. Hence the sum in (1) makes sense and is finite.

Note 2. This sum is also independent of the particular choice of $\{A_{i}\}.$ For if $\{B_{k}\}$ is another $\mathcal{M}$-partition of $A,$ with $f=b_{k}$ on $B_{k},$ say, then $f=a_{i}=b_{k}$ on $A_{i} \cap B_{k}$ whenever $A_{i} \cap B_{k} \neq \emptyset.$ Also,

$$(\forall i) \quad A_{i}=\bigcup_{k}\left(A_{i} \cap B_{k}\right) \text { (disjoint);}$$

so

$$(\forall i) \quad a_{i} m A_{i}=\sum_{k} a_{i} m(A_{i} \cap B_{k}),$$

and hence (see Theorem 2 of Chapter 7, §2, and Problem 11 there)

$$\sum_{i} a_{i} m A_{i}=\sum_{i} \sum_{k} a_{i} m\left(A_{i} \cap B_{k}\right)=\sum_{k} \sum_{i} b_{k} m\left(A_{i} \cap B_{k}\right)=\sum_{k} b_{k} m B_{k}.$$

(Explain!)

This makes our definition (1) unambiguous and allows us to choose any $\mathcal{M}$-partition $\{A_{i}\},$ with $f$ constant on each $A_{i},$ when forming integrals (1).

Corollary $\PageIndex{1}$

Let $f : S \rightarrow E$ be elementary and integrable on $A \in \mathcal{M}.$ Then the following statements are true.

(i) $|f|<\infty$ a.e. on $A.$

(ii) $f$ and $|f|$ are elementary and integrable on any $\mathcal{M}$-set $B \subseteq A,$ and

$$\left|\int_{B} f\right| \leq \int_{B}|f| \leq \int_{A}|f|.$$

(iii) The set $B=A(f \neq 0)$ is $\sigma$-finite (Definition 4 in Chapter 7, §5), and

$$\int_{A} f=\int_{B} f.$$

(iv) If $f=a$ (constant) on $A$,

$$\int_{A} f=a \cdot m A.$$

(v) $\int_{A}|f|=0$ iff $f=0$ a.e. on $A$.

(vi) If $m Q=0,$ then

$$\int_{A} f=\int_{A-Q} f$$

(so we may neglect sets of measure 0 in integrals).

(vii) For any $k$ in the scalar field of $E, k f$ is elementary and integrable, and

$$\int_{A} k f=k \int_{A} f.$$

Note that if $f$ is scalar valued, $k$ may be a vector. If $E=E^{*},$ we assume $k \in E^{1}.$

Proof

(i) By Note 1, $|f|=|a_{i}|=\infty$ only on those $A_{i}$ with $m A_{i}=0.$ Let $Q$ be the union of all such $A_{i}.$ Then $m Q=0$ and $|f|<\infty$ on $A-Q,$ proving (i).

(ii) If $\{A_{i}\}$ is an $\mathcal{M}$-partition of $A,\{B \cap A_{i}\}$ is one for $B.$ (Verify!) We have $f=a_{i}$ and $|f|=|a_{i}|$ on $B \cap A_{i} \subseteq A_{i}$.

Also,

$$\sum\left|a_{i}\right| m\left(B \cap A_{i}\right) \leq \sum\left|a_{i}\right| m A_{i}<\infty.$$

(Why?) Thus $f$ and $|f|$ are elementary and integrable on $B,$ and (ii) easily follows by formula (1).

(iii) By Note 1, $f=0$ on $A_{i}$ if $m A_{i}=\infty.$ Thus $f \neq 0$ on $A_{i}$ only if $m A_{i}<\infty$. Let $\{A_{i_{k}}\}$ be the subsequence of those $A_{i}$ on which $f \neq 0;$ so

$$(\forall k) \quad m A_{i_{k}}<\infty.$$

Also,

$$B=A(f \neq 0)=\bigcup_{k} A_{i_{k}} \in \mathcal{M} \text{ (}\sigma \text {-finite!).}$$

By (ii), $f$ is elementary and integrable on $B.$ Also,

$$\int_{B} f=\sum_{k} a_{i_{k}} m A_{i_{k}},$$

while

$$\int_{A} f=\sum_{i} a_{i} m A_{i}.$$

These sums differ only by terms with $a_{i}=0.$ Thus (iii) follows.

The proof of (iv)-(vii) is left to the reader.$\quad \square$

Note 3. If $f : S \rightarrow E^{*}$ is elementary and sign-constant on $A,$ we also allow that

$$\int_{A} f=\sum_{i} a_{i} m A_{i}=\pm \infty.$$

Thus here $\int_{A} f$ exists even if $f$ is not integrable. Apart from claims of integrability and $\sigma$-finiteness, Corollary 1(ii)-(vii) hold for such $f$, with the same proofs.

Example

Let $m$ be Lebesgue measure in $E^{1}.$ Define $f=1$ on $R$ (rationals) and $f=0$ on $E^{1}-R ;$ see Chapter 4, §1, Example (c). Let $A=[0,1].$

By Corollary 1 in Chapter 7, §8, $A \cap R \in \mathcal{M}^{*}$ and $m(A \cap R)=0.$ Also, $A-R \in \mathcal{M}^{*}$.

Thus $\{A \cap R, A-R\}$ is an $\mathcal{M}^{*}$-partition of $A,$ with $f=1$ on $A \cap R$ and $f=0$ on $A-R.$

Hence $f$ is elementary and integrable on $A,$ and

$$\int_{A} f=1 \cdot m(A \cap R)+0 \cdot m(A-R)=0.$$

Thus $f$ is L-integrable (even though it is nowhere continuous).

Theorem $\PageIndex{1}$ (additivity)

(i) If $f : S \rightarrow E$ is elementary and integrable or elementary and nonnegative on $A \in \mathcal{M},$ then

$$\int_{A} f=\sum_{k} \int_{B_{k}} f$$

for any $\mathcal{M}$-partition $\left\{B_{k}\right\}$ of $A$.

(ii) If $f$ is elementary and integrable on each set $B_{k}$ of a finite $\mathcal{M}$-partition

$$A=\bigcup_{k} B_{k},$$

it is elementary and integrable on all of $A,$ and (2) holds again.

Proof

(i) If $f$ is elementary and integrable or elementary and nonnegative on $A=\bigcup_{k} B_{k},$ it is surely so on each $B_{k}$ by Corollary 2 of §1 and Corollary 1(ii) above.

Thus for each $k,$ we can fix an $\mathcal{M}$-partition $B_{k}=\bigcup_{i} A_{k i},$ with $f$ constant $(f=a_{k i})$ on $A_{k i}, i=1,2, \ldots$. Then

$$A=\bigcup_{k} B_{k}=\bigcup_{k} \bigcup_{i} A_{k i}$$

is an $\mathcal{M}$-partition of $A$ into the disjoint sets $A_{k i} \in \mathcal{M}$.

Now, by definition,

$$\int_{B_{k}} f=\sum_{i} a_{k i} m A_{k i}$$

and

$$\int_{A} f=\sum_{k, i} a_{k i} m A_{k i}=\sum_{k}\left(\sum_{i} a_{k i} m A_{k i}\right)=\sum_{k} \int_{B_{k}} f$$

by rules for double series. This proves formula (2).

(ii) If $f$ is elementary and integrable on $B_{k}(k=1, \ldots, n),$ then with the same notation, we have

$$\sum_{i}\left|a_{k i}\right| m A_{k i}<\infty$$

(by integrability); hence

$$\sum_{k=1}^{n} \sum_{i}\left|a_{k i}\right| m A_{k i}<\infty.$$

This means, however, that $f$ is elementary and integrable on $A,$ and so clause (ii) follows.$\quad \square$

Caution. Clause (ii) fails if the partition $\{B_{k}\}$ is infinite.

Theorem $\PageIndex{2}$

(i) If $f, g : S \rightarrow E^{*}$ are elementary and nonnegative on $A,$ then

$$\int_{A}(f+g)=\int_{A} f+\int_{A} g.$$

(ii) If $f, g : S \rightarrow E$ are elementary and integrable on $A,$ so is $f \pm g,$ and

$$\int_{A}(f \pm g)=\int_{A} f \pm \int_{A} g.$$

Proof

Arguing as in the proof of Theorem 1 of §1, we can make $f$ and $g$ constant on sets of one and the same $\mathcal{M}$-partition of $A,$ say, $f=a_{i}$ and $g=b_{i}$ on $A_{i} \in \mathcal{M};$ so

$$f \pm g=a_{i} \pm b_{i} \text { on } A_{i}, \quad i=1,2, \ldots.$$

In case (i), $f, g \geq 0;$ so integrability is irrelevant by Note 3, and formula (1) yields

$$\int_{A}(f+g)=\sum_{i}\left(a_{i}+b_{i}\right) m A_{i}=\sum_{i} a_{i} m A_{i}+\sum b_{i} m A_{i}=\int_{A} f+\int_{A} g.$$

In (ii), we similarly obtain

$$\sum_{i}\left|a_{i} \pm b_{i}\right| m A_{i} \leq \sum\left|a_{i}\right| m A_{i}+\sum_{i}\left|b_{i}\right| m A_{i}<\infty.$$

(Why?) Thus $f \pm g$ is elementary and integrable on $A.$ As before, we also get

$$\int_{A}(f \pm g)=\int_{A} f \pm \int_{A} g,$$

simply by rules for addition of convergent series. (Verify!)$\quad \square$

Note 4. As we know, the characteristic function $C_{B}$ of a set $B \subseteq S$ is defined

$$C_{B}(x)=\left\{\begin{array}{ll}{1,} & {x \in B,} \\ {0,} & {x \in S-B.}\end{array}\right.$$

If $g : S \rightarrow E$ is elementary on $A,$ so that

$$g=a_{i} \text { on } A_{i}, 1,2, \ldots,$$

for some $\mathcal{M}$-partition

$$A=\bigcup A_{i},$$

then

$$g=\sum_{i} a_{i} C_{A_{i}} \text { on } A.$$

(This sum always exists for disjoint sets $A_{i}.$ Why?) We shall often use this notation.

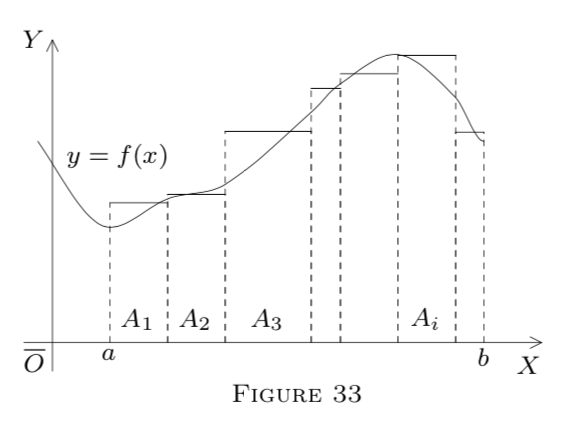
If $m$ is Lebesgue measure in $E^{1},$ the integral

$$\int_{A} g=\sum_{i} a_{i} m A_{i}$$

has a simple geometric interpretation; see Figure 33. Let $A=[a, b] \subset E^{1};$ let $g$ be bounded and nonnegative on $E^{1}.$ Each product $a_{i} m A_{i}$ is the area of a rectangle with base $A_{i}$ and altitude $a_{i}.$ (We assume the $A_{i}$ to be intervals here.) The total area,

$$\int_{A} g=\sum_{i} a_{i} m A_{i},$$

can be treated as an approximation to the area under some curve $y=f(x)$, where $f$ is approximated by $g$ (Theorem 3 in §1). Integration historically arose from such approximations.

Integration of elementary extended-real functions. Note 3 can be extended to sign-changing functions as follows.

Definition

If

$$f=\sum_{i} a_{i} C_{A_{i}} \quad\left(a_{i} \in E^{*}\right)$$

on

$$A=\bigcup_{i} A_{i} \quad\left(A_{i} \in \mathcal{M}\right),$$

we set

$$\int_{A} f=\int_{A} f^{+}-\int_{A} f^{-},$$

with

$$f^{+}=f \vee 0 \geq 0 \text { and } f^{-}=(-f) \vee 0 \geq 0;$$

see §2.

By Theorem 2 in §2, $f^{+}$ and $f^{-}$ are elementary and nonnegative on $A;$ so

$$\int_{A} f^{+} \text { and } \int_{A} f^{-}$$

are defined by Note 3, and so is

$$\int_{A} f=\int_{A} f^{+}-\int_{A} f^{-}$$

by our conventions (2*) in Chapter 4, §4.

We shall have use for formula (3), even if

$$\int_{A} f^{+}=\int_{A} f^{-}=\infty;$$

then we say that $\int_{A} f$ is unorthodox and equate it to $+\infty,$ by convention; cf. Chapter 4, §4. (Other integrals are called orthodox.) Thus for elementary and (extended) real functions, $\int_{A} f$ is always defined. (We further develop this idea in §5.)

Note 5. With $f$ as above, we clearly have

$$f^{+}=a_{i}^{+} \text { and } f^{-}=a_{i}^{-} \text { on } A_{i},$$

where

$$a_{i}^{+}=\max \left(a_{i}, 0\right) \text { and } a_{i}^{-}=\max \left(-a_{i}, 0\right).$$

Thus

$$\int_{A} f^{+}=\sum a_{i}^{+} \cdot m A_{i} \text { and } \int_{A} f^{-}=\sum a_{i}^{-} \cdot m A_{i},$$

so that

$$\int_{A} f=\int_{A} f^{+}-\int_{A} f^{-}=\sum_{i} a_{i}^{+} \cdot m A_{i}-\sum_{i} a_{i}^{-} \cdot m A_{i}.$$

If $\int_{A} f^{+}<\infty$ or $\int_{A} f^{-}<\infty,$ we can subtract the two series termwise (Problem 14 of Chapter 4, §13) to obtain

$$\int_{A} f=\sum_{i}\left(a_{i}^{+}-a_{i}^{-}\right) m A_{i}=\sum_{i} a_{i} m A_{i}$$

for $a_{i}^{+}-a_{i}^{-}=a_{i}.$ Thus formulas (3) and (4) agree with our previous definitions.