1.4: Complex Numbers

Our number system can be subdivided in many different ways. The most basic form of mathematics is counting and almost all human cultures have words to represent numbers (the Pirahã of South America are a notable exception). Thus the most basic set of numbers is the set of counting numbers represented by the double barred $\mathrm{N}: \mathbb{N}=\{1,2,3,4,5,6,7, \ldots\}$ (we will set aside the debate as to whether or not zero should be included in this set).

If we try to subtract a larger counting number from a smaller counting number we find that there are no members in the set of counting numbers to represent the answer in this situation. This extends the set of natural numbers to the set of integers: $\mathbb{Z}=\{\ldots,-3,-2,-1,0,1,2,3, \ldots\} .$ The integers are represneted by the double barred $Z$, for the German word for numbers-"zahlen." In the earliest appearances of negative numbers in the Chinese and Indian mathematical systems, negative values were often used to represent debt. Because Greek mathematics was based on Geometry, they did not use negative numbers.

Moving to multiplication and division, if we question the value of $8 \div 2=4$ versus $8 \div 3=?,$ we once again must expand our conception of numbers to allow for an answer to the second question $8 \div 3=?$. Understanding ratios of whole numbers or Rational numbers allows solutions to such problems. The set of Rational numbers is represented by the double barred $Q$, to represent a quotient:
$\mathbb{Q}=\left\{\frac{a}{b}: a, b \in \mathbb{Z}\right\}$

The Greek understanding of numbers mostly stopped here. They felt that all quantities could be represented as the ratio of whole numbers. The length of the diagonal of a square whose sides are of length 1 produced considerable consternation among the Pythagoreans as a result of this. Using the Pythagorean Theorem for the diagonal of a square whose sides are of length 1 shows that the diagonal would be $c^{2}=1^{2}+1^{2}=2,$ thus $c=\sqrt{2} .$ This number cannot be represented as a ratio of whole numbers. This new class of numbers adds the set
of irrational numbers to the existing set of rational numbers to create the Real numbers, represented with a double barred $\mathrm{R}$ : $\mathbb{R}$.

This hierarchy of numbers is often represented in the following diagram:

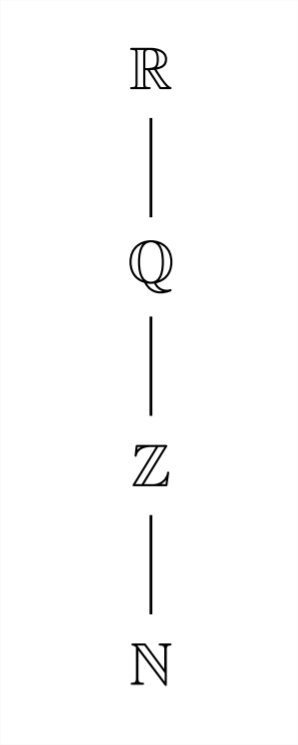
One of the best ways to conceptualize the Real number system is on the number line - every point on the number line corresponds to a unique Real number and every Real number corresponds to a unique position on the Real number line.

After the development of the printing press in the 15 th century, Fibonacci's Liber Abaci was translated into Italian from Latin and read throughout Italy. As a result, Italy became a thriving center of mathematics until the 17 th century, when the center of European mathematics moved north to France, Germany and England.

Throughout the 1500 's Italian mathematicians such as Girolamo Cardano, Raphael Bombelli and Niccolo Fontana Tartaglia worked to extend the ideas in Fibonacci's book. They produced formulas to solve cubic ( $x^{3}$ ), and quartic ( $x^{4}$ ) degree equations. In solving some of these equations they found that their formulas sometimes produced negative values under a square root. None of the known number systems could accomodate this possibility. In Cardano's book on algebra Ars Magna, he encounters a problem which involves the square root of a negative number. He says, "It is clear that this case is impossible. Nevertheless we will work thus..." and he proceeds to compute a valid complex solution to the problem. Mathematicians eventually defined the complex unit $\sqrt{-1}=i$ and then

devised a system in which all complex numbers are a combination of a Real part
$(a)$ and an "imaginary" part (bi).
The complex numbers are a two dimensional number system represented by the double barred $C: \mathbb{C}=\{a+b i: a, b \in \mathbb{R}\},$ where $i$ is the complex unit defined as $i=\sqrt{-1} .$ Throughout the late 1700 's and early 1800 's mathematicians gradually moved towards a geometrical interpretation of the two-dimensional complex numbers. What is today known as the "Argand diagram" represents the real valued portion of a complex number along a horizontal axis and the multiple of the complex unit along the vertical axis.

Expressing square roots of negative numbers

Square roots of negative quantities are generally expressed as a multiple of $i$

Example $\PageIndex{1}$

$$\begin{array}{c} \sqrt{-4}=2 i \\ \sqrt{-25}=5 i \\ \sqrt{-7} \approx 2.646 i \end{array}$$

Adding, subtracting and multiplying with complex numbers

Calculating with complex numbers has many similarities to working with variables. The real part and imginary part are treated separately for addition and subtraction, but can be multiplied and divided.

Example $\PageIndex{2}$

Compute the following:

$$\begin{array}{c} (6-4 i)+(-2+7 i)=4+3 i \\ (-9+2 i)-(-4+6 i)=-9+2 i+4-6 i=-5-4 i \\ 3(10+i)=30+3 i \\ -7 i(-5+8 i)=35 i-56 i^{2} \end{array}$$

Now we encounter an interesting fact about complex numbers and, in particular, the complex unit $i .$ By definition, $i=\sqrt{-1} .$ Therefore, if we square $i$ we should get $-1 .$ In the last example problem above, we can replace the $i^{2}$ with -1 to finish the problem.

$$\begin{aligned} -7 i(-5+8 i) &=35 i-56 i^{2} \\ &=35 i-56(-1) \\ &=35 i+56 \\ &=56+35 i \end{aligned}$$

Example $\PageIndex{3}$

Compute the following:

$$\begin{aligned} (8-5 i)(1-4 i) &=8-32 i-5 i+20 i^{2} \\ &=8-37 i+20(-1) \\ &=8-37 i-20 \\ &=-12-37 i \\ \\ (9+2 i)^{2} &=(9+2 i)(9+2 i) \\ &=81+18 i+18 i+4 i^{2} \\ &=81+36 i+4(-1) \\ &=81+36 i-4 \\ &=77+36 i \end{aligned}$$

Powers of $i$

The powers of $i$ follow an interesting pattern based on the definition that $i^{2}=-1$
We can see that $i^{1}=i$ and that $i^{2}=-1,$ as a result, $i^{3}=i^{2} * i^{1}=-1 * i=-i$
In a similar fashion, $i^{4}=i^{2} * i^{2}=(-1)(-1)=1$
This means that $i^{5}=i^{4} * i=1 * i=i$
If we put all of this information together we get the following:
$i^{1}=i$
$i^{2}=-1$
$i^{3}=-i$
$i^{4}=1$
$i^{5}=i^{1}=i$
$i^{6}=i^{2}=-1$
$i^{7}=i^{3}=-i$
$i^{8}=i^{4}=1$
In other words, every power of $i$ is equivalent to either $i,-1,-i,$ or $1 .$ To determine which of these values a power of $i$ is equivalent to, we need to find the remainder of the exponent when it is divided by 4

Example $\PageIndex{4}$

Simplify $i^{38}$

Solution

since every $i^{4}=1,$ then $i^{38}=i^{36} * i^{2}=\left(i^{4}\right)^{9} * i^{2}=1^{9} * i^{2}=i^{2}=-1$
since 38 is 2 more than a multiple of $4,$ then $i^{38}=i^{2}=-1$

Exercise $\PageIndex{1}$

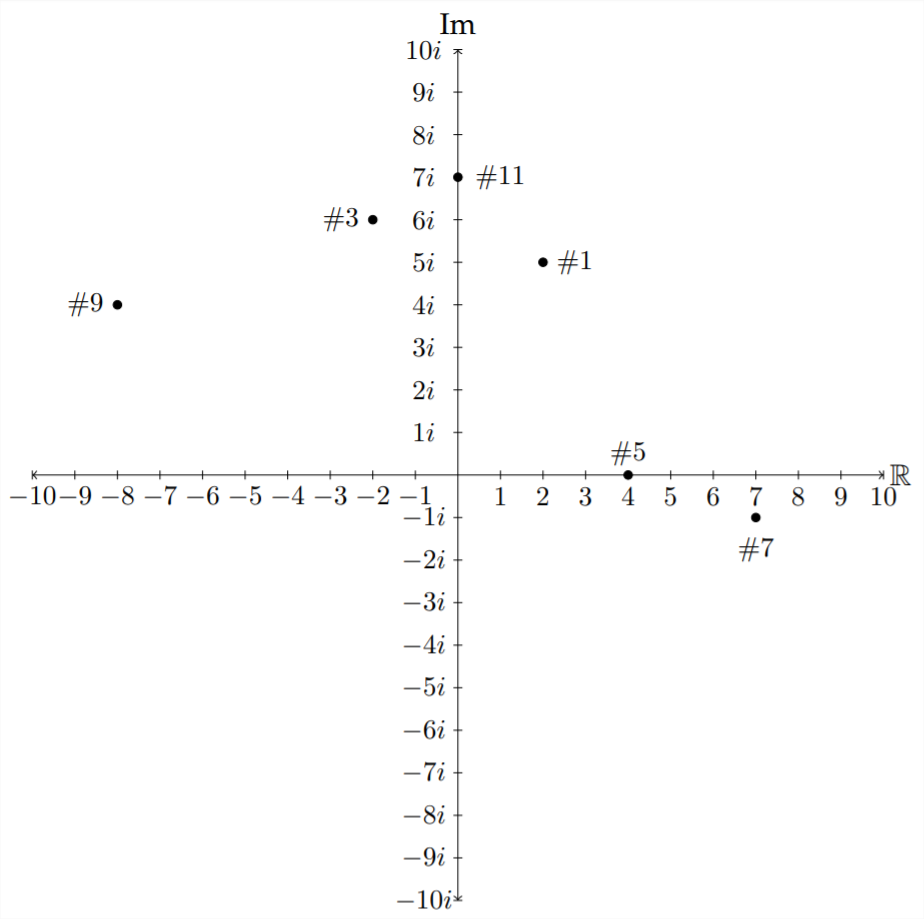
Graph the following complex numbers:

1) $\quad 2+5 i$
2) $\quad 4-3 i$
3) $\quad -2+6 i$
4) $\quad -3-5 i$
5)$\quad 4$
6) $\quad -2 i$
7) $\quad 7-i$
8) $\quad -1+i$
9) $\quad -8+4 i$
10)$\quad 8+3 i$
11) $\quad 7 i$
12) $\quad -5-9 i$

Express each quantity in terms of $i .$ Round irrational values to the nearest 1000 th.
13) $\quad \sqrt{-36}$
14) $\quad \sqrt{-81}$
15) $\quad \sqrt{-100}$
16) $\quad \sqrt{-49}$
17) $\quad \sqrt{-4}$
18) $\quad \sqrt{-25}$
19) $\quad \sqrt{-2}$
20)$\quad \sqrt{-6}$
21) $\quad \sqrt{-10}$
22) $\quad \sqrt{-31}$
23) $\quad \sqrt{-5}$
24) $\quad \sqrt{-3}$

Perform the indicated operation and simplify
25) $\quad(6+7 i)+(5+3 i)$
26) $\quad(4-5 i)+(3+9 i)$
27) $\quad(9+8 i)-(1-2 i)$
28) $\quad(2+i)-(6-4 i)$
29) $\quad(7-4 i)-(5-3 i)$
30) $\quad(8+i)-(4+3 i)$
31) $\quad(7 i)(6 i)$
32) $\quad(4 i)(-8 i)$
33) $\quad(-2 i)(5 i)$
34) $\quad(12 i)(3 i)$
35) $\quad(1+i)(3+2 i)$
36) $\quad(1+5 i)(4+3 i)$
37) $\quad(6-5 i)(2-3 i)$
38) $\quad(8-3 i)(2+i)$
39) $\quad(-3+4 i)(-1-2 i)$
40) $\quad(-7-i)(3-5 i)$
41) $\quad(4-2 i)^{2}$
42) $\quad(-5+i)^{2}$
43) $\quad(3+i)(3-i)$
44) $\quad(2+6 i)(2-6 i)$
45) $\quad(9-4 i)(9+4 i)$
46) $\quad(5+2 i)(5-2 i)$

Express as either $i,-1,-i,$ or 1
47)$\quad i^{3}$
48)$\quad i^{7}$
49) $\quad i^{21}$
50)$\quad i^{13}$
51) $\quad i^{29}$
52) $\quad i^{56}$
53) $\quad i^{72}$
54)$\quad i^{35}$
55) $\quad i^{66}$
56)$\quad i^{103}$
57)$\quad i^{16}$
58)$\quad i^{53}$
59)$\quad i^{11}$
60)$\quad i^{42}$
61) $\quad i^{70}$
62)$\quad i^{9}$

Answer

13) $\quad 6 i$
15) $\quad 10 i$
17) $\quad 2 i$
19) $\quad 1.414 i$
21) $\quad 3.162 i$
23) $\quad 2.236 i$
25) $\quad 11+10 i$
27) $\quad 8+10 i$
29) $\quad 2-i$
31) $\quad-42$
33) $\quad 10$
35) $\quad 1+5 i$
37) $\quad-3-28 i$
39) $\quad 11+2 i$
41)$\quad 12-16 i$
43) $\quad 10$
45) $\quad 97$
47)$\quad -i$
49)$\quad i$
51) $\quad i$
53) $\quad 1$
55) $\quad -1$
57) $\quad 1$
59) $\quad -i$
61) $\quad -1$