7.2: Graphing Linear Equations and Inequalities in One Variable
( \newcommand{\kernel}{\mathrm{null}\,}\)
Graphs
We have, thus far in our study of algebra, developed and used several methods for obtaining solutions to linear equations in both one and two variables. Quite often it is helpful to obtain a picture of the solutions to an equation. These pictures are called graphs and they can reveal information that may not be evident from the equation alone.
The geometric representation (picture) of the solutions to an equation is called the graph of the equation.
Axes, Coordinate Systems, and Dimension
Axis
The basic structure of the graph is the axis. It is with respect to the axis that all solutions to an equation are located. The most fundamental type of axis is the number line.
The Number Line is an Axis

We have the following general rules regarding axes.
Number of Variables and Number of Axes
- An equation in one variable requires one axis.
- An equation in two variables requires two axes.
- An equation in three variables requires three axes.
- ... An equation in nn variables requires nn axes.
We shall always draw an axis as a straight line, and if more than one axis is required, we shall draw them so they are all mutually perpendicular (the lines forming the axes will be at 90° angles to one another).
A system of axes constructed for graphing an equation is called a coordinate system.
The Phrase, Graphing an EquationThe phrase graphing an equation is used frequently and should be interpreted as meaning geometrically locating the solutions to an equation.
Relating the Number of Variables and the Number of Axes
We will not start actually graphing equations until Section 7.3, but in the following examples, we will relate the number of variables in an equation to the number of axes in the coordinate system.
1. One-Dimensional Graphs:
- If we wish to graph the equation 5x+2=17, we would need to construct a coordinate system consisting of a single axis (a single number line) since the equation consists of only one variable. We label the axis with the variable that appears in the equation.
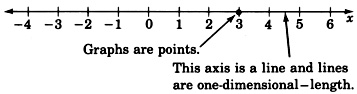
- We might interpret an equation in one variable as giving information in one-dimensional space. Since we live in three-dimensional space, one-dimensional space might be hard to imagine. Objects in one-dimensional space would have only length, no width or depth.
2. Two-Dimensional Graphs:
To graph an equation in two variables such as y=2x–3y, we would need to construct a coordinate system consisting of two mutually perpendicular number lines (axes). We call the intersection of the two axes the origin and label it with a 0. The two axes are simply number lines; one drawn horizontally, one drawn vertically.
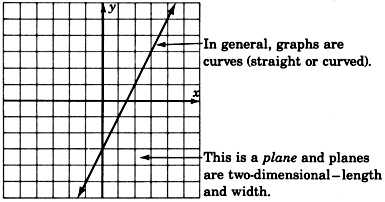
Recall that an equation in two variables requires a solution to be a pair of numbers. The solutions can be written as ordered pairs (x,y). Since the equation y=2x–3 involves the variables x and y, we label one axis x and the other axis y. In mathematics, it is customary to label the horizontal axis with the independent variable and the vertical axis with the dependent variable.
We might interpret equations in two variables as giving information in two-dimensional space. Objects in two-dimensional space would have length and width, but no depth.
3. Three-Dimensional Graphs:
An equation in three variables, such as 3x2–4y2+5z=0, requires three mutually perpendicular axes, one for each variable. We would construct the following coordinate system and graph.
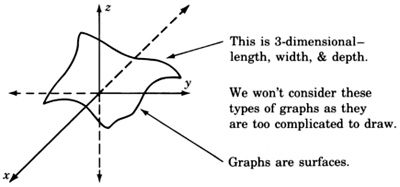
We might interpret equations in three variables as giving information about three-dimensional space.
4. Four-Dimensional Graphs
To graph an equation in four variables, such as 3x–2y+8x–5w=–7, would require four mutually perpendicular number lines. These graphs are left to the imagination.
We might interpret equations in four variables as giving information in four-dimensional space. Four-dimensional objects would have length, width, depth, and some other dimension.
Black Holes
These other spaces are hard for us to imagine, but the existence of “black holes” makes the possibility of other universes of one-, two-, four-, or n-dimensions not entirely unlikely. Although it may be difficult for us “3-D” people to travel around in another dimensional space, at least we could be pretty sure that our mathematics would still work (since it is not restricted to only three dimensions)!
Graphing in One Dimension
Graphing a linear equation in one variable involves solving the equation, then locating the solution on the axis (number line), and marking a point at this location. We have observed that graphs may reveal information that may not be evident from the original equation. The graphs of linear equations in one variable do not yield much, if any, information, but they serve as a foundation to graphs of higher dimension (graphs of two variables and three variables).
Sample Set A
Graph the equation 3x–5=10.
Solve the equation for x and construct an axis. Since there is only one variable, we need only one axis. Label the axis x.
3x−5=103x=15x=5
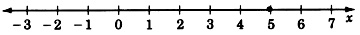
Graph the equation 3x+4+7x−1+8=31.
Solving the equation we get,
10x+11=3110x+20x=2
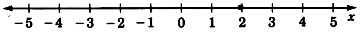
Practice Set A
Graph the equation 4x+1=−7

- Answer
-
x=−2
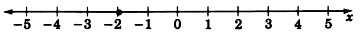
Sample Set B
Graph the linear inequality 4x/ge12.
We proceed by solving the inequalioty.
4x≥12Divide each side by 4x≥3
As we know, any value greater than or equal to 3 will satisfy the original inequality. Hence we have infinitely many solutions and, thus, infinitely many points to mark off on our graph.
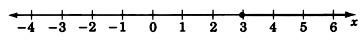
The closed circle at 3 means that 3 is included as a solution. All the points beginning at 3 and in the direction of the arrow are solutions.
Graph the linear inequality −2y−1>3.
We first solve the inequality.
−2y−1>3−2y>4y<−2 The inequality symbol reversed direction because we divided by −2
Thus, all numbers strictly less than −2 will satisfy the inequality and are thus solutions.
Since −2 itself is not to be included as a solution, we draw an open circle at −2. The solutions are to the left of −2 so we draw an arrow pointing to the left of −2 to denote the region of solutions.
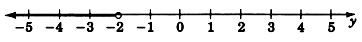
Graph the inequality −2≤y+1<1.
We recognize this inequality as a compound inequality and solve it by subtracting 1 from all three parts.
−2≤y+1<1−3≤y<0
Thus, the solution is all numbers between −3 and 0, more precisely, all numbers greater than or equal to −3 but strictly less than 0.

Graph the linear equation 5x=−125.
The solution is x=−25. Scaling the axis by units of 5 rather than 1, we obtain
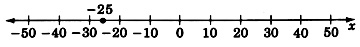
Practice Set B
Graph the inequality 3x≤18

- Answer
-
x≤6

Graph the inequality −3m+1<13.

- Answer
-
m>−4
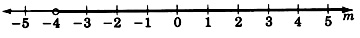
Graph the inequality −3≤x−5<5.

- Answer
-
2≤x<10

Graph the linear equation −6y=480.

- Answer
-
y=−80
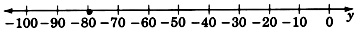
Exercises
For problems 1 - 25, graph the linear equations and inequalities.
4x+7=19

- Answer
-
x=3
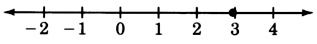
8x−1=7

2x+3=4

- Answer
-
x=12

x+3=15

6y+3=y+8

- Answer
-
y=1

2x=0

4+1−4=3z

- Answer
-
z=13

x+12=43

7r=14

- Answer
-
r=128

2x−6=25

x+7≤12

- Answer
-
x≤5
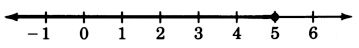
y−5<3

x+19>2

- Answer
-
x>−17
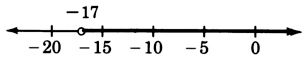
z+5>11

3m−7≤8

- Answer
-
m≤5
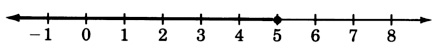
−5t≥10

−8x−6≥34

- Answer
-
x≤−5
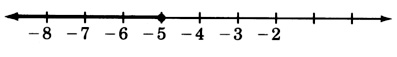
x4<2

y7≤3

- Answer
-
y≤21
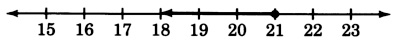
2y9≥4

−5y8≤4

- Answer
-
y≥−325
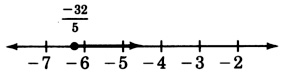
−6a7<−4

−1≤x−3<0

- Answer
-
2≤x<3

6≤x+4≤7

−12<−2x−2≤−8

- Answer
-
3≤x<5

Exercises for Review
Simplify (3x8y2)3.
List, if any should appear, the common factors in the expression 10x4−15x2+5x6.
- Answer
-
5x2
Solve the inequality −4(x+3)<−3x+1.
Solve the equation y=−5x+8 if x=−2.
- Answer
-
(−2,18)
Solve the equation 2y=5(3x+7) if x=−1.


