7.5: The Slope-Intercept Form of a Line
- Page ID
- 49384
The General Form of a Line
We have seen that the general form of a linear equation in two variables is ax+by=c (Section 7.4). When this equation is solved for y, the resulting form is called the slope-intercept form. Let's generate this new form.
\(\begin{aligned}
ax + by &=c&\text{Subtract } ax \text{ from both sides. }\\
by &= -ax + c&\text{ Divide both sides by } b\\
\dfrac{by}{b} &= \dfrac{-ax}{b} + \dfrac{c}{b}\\
\dfrac{\not{b}y}{\not{b}}&= \dfrac{-ax}{b} + \dfrac{c}{b}\\
y&=\dfrac{-ax}{b} + \dfrac{c}{b}\\
\end{aligned}\)
This equation is of the form \(y = mx + b\) if we replace \(\dfrac{-a}{b}\) with \(m\) and constant \(\dfrac{c}{b}\) with \(b\). (Note The fact that we let \(b = \dfrac{c}{b}\) is unfortunate and occurs because of the letters we have chosen to use in the general form. The letter \(b\) occurs on both sides of the equal sign and may not represent the same value at all. This problem is one of the historical convention and, fortunately, does not occur very often.)
The following examples illustrate this procedure.
Solve \(3x + 2y = 6\) for \(y\).
\(\begin{aligned}
3x + 2y&= 6& \text{ Subtract } 3x \text{ from both sides }\\
2y&= -3x + 6& \text{ Divide both sides by } 2\\
y &= -\dfrac{3}{2}x + 3
\end{aligned}\)
The equation is of the form \(y = mx + b\). In this case, \(m = -\dfrac{3}{2}\) and \(b = 3\).
Solve \(-15x + 5y = 20\) for \(y\).
\(\begin{aligned}
-15x + 5y&=20\\
5y&=15x + 20\\
y&=3x+4
\end{aligned}\)
This equation is of the form \(y = mx + b\). In this case, \(m = 3\) and \(b = 4\).
Solve \(4x-y = 0\) for \(y\).
\(\begin{aligned}
4x-y&=0\\
-y&=-4x\\
y&=4x
\end{aligned}\)
This equation is of the form \(y = mx + b\). In this case, \(m=4\) and \(b=0\). Notice that we can write \(y=4x\) as \(y = 4x + 0\)
The Slope-Intercept Form of a Line
The Slope-Intercept Form of a Line \(y=mx+b\)
A linear equation in two variables written in the form \(y=mx+b\) is said to be in slope-intercept form.
Sample Set A
The following equations are in slope-intercept form:
\(y = 6x - 7\). In this case \(m = 6\) and \(b = -7\)
\(y = -2x + 9\). In this case \(m = -2\) and \(b = 9\)
\(y = \dfrac{1}{5}x + 4.8\). In this case \(m = \dfrac{1}{5}\) and \(b = 4.8\)
\(y = 7x\). In this case \(m = 7\) and \(b = 0\) since we can write \(y = 7x\) as \(y = 7x + 0\).
The following equations are not in slope-intercept form.
\(2y = 4x - 1\). The coefficient of \(y\) is \(2\). To be in slope-intercept form, the coefficient of \(y\) must be \(1\).
\(y + 4x = 5\). The equation is not solved for \(y\). THe \(x\) and \(y\) appear on the same side of the equal sign.
\(y + 1 = 2x\). The equation is not solved for \(y\)
Practice Set A
The following equation are in slope-intercept form. In each case, specify the slope and \(y\)-intercept.
\(y=2x+7; m=?, b=?\)
- Answer
-
\(m=2, b=7\)
\(y=−4x+2; m=?, b=?\)
- Answer
-
\(m=−4,b=2\)
\(y=−5x−1; m=?, b=?\)
- Answer
-
\(m=−5,b=−1\)
\(y=\dfrac{2}{3}x−10; m=?, b=?\)
- Answer
-
\(m = \dfrac{2}{3}, b = -10\)
\(y = \dfrac{-5}{8}x + \dfrac{1}{2}; m=?, b=?\)
- Answer
-
\(m = \dfrac{-5}{8}, b=\dfrac{1}{2}\)
\(y=−3x; m=?, b=?\)
- Answer
-
\(m=−3, b=0\)
Slope and Intercept
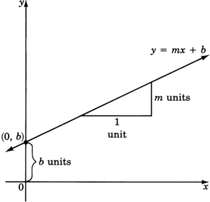
When the equation of a line is written in slope-intercept form, two important properties of the line can be seen: the slope and the intercept. Let's look at these two properties by graphing several lines and observing them carefully.
Sample Set B
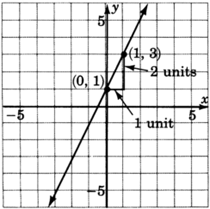
Graph the line \(y=x−3\).
| \(x\) | \(y\) | \((x, y)\) |
| \(0\) | \(−3\) | \((0, −3)\) |
| \(4\) | \(1\) | \((4, 1)\) |
| \(−2\) | \(−5\) | \((−2, −5)\) |
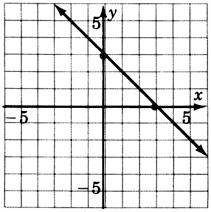
Looking carefully at this line, answer the following two questions.
At what number does this line cross the y-axis? Do you see this number in the equation?
The line crosses the y-axis at −3.
Place your pencil at any point on the line. Move your pencil exactly one unit horizontally to the right. Now, how many units straight up or down must you move your pencil to get back on the line? Do you see this number in the equation?
After moving horizontally one unit to the right, we must move exactly one vertical unit up. This number is the coefficient of \(x\).
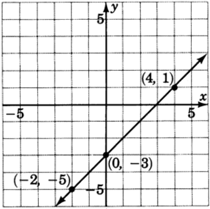
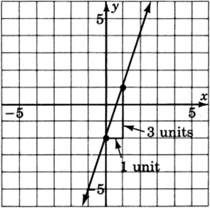
Graph the line \(y = \dfrac{2}{3}x + 1\)
| \(x\) | \(y\) | \((x, y)\) |
| \(0\) | \(1\) | \((0, 1)\) |
| \(3\) | \(3\) | \((3, 3)\) |
| \(−3\) | \(−1\) | \((−3, −1)\) |
Looking carefully at this line, answer the following two questions.
At what number does this line cross the \(y\)-axis? Do you see this number in the equation?
The line crosses the \(y\)-axis at \(+1\).
Place your pencil at any point on the line. Move your pencil exactly one unit horizontally to the right. Now, how many units straight up or down must you move your pencil to get back on the line? Do you see this number in the equation?
After moving horizontally one unit to the right, we must move exactly \(\dfrac{2}{3}\) unit upward. This number is the coefficient of \(x\).
Practice Set B
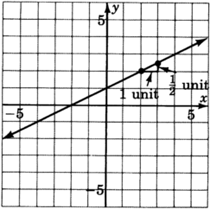
Graph the line \(y = -3x + 4\)
| \(x\) | \(y\) | \((x, y)\) |
| \(0\) | - | - |
| \(3\) | - | - |
| \(2\) | - | - |
Looking carefully at this line, answer the following two questions.
At what number does the line cross the \(y\)-axis? Do you see this number in the equation?
- Answer
-
The line crosses the \(y\)-axis at \(+4\). After moving horizontally \(1\) unit to the right, we must move exactly \(3\) units downward.
Place your pencil at any point on the line. Move your pencil exactly one unit horizontally to the right. Now, how many units straight up or down must you move your pencil to get back on the line? Do you see this number in the equation?
- Answer
-
In the graphs constructed in Sample Set B and Practice Set B, each equation had the form \(y=mx+b\). We can answer the same questions by using this form of the equation (shown in the diagram).
\(y\)-Intercept
At what number does the line cross the \(y\)-axis? Do you see this number in the equation?
- Answer
-
In each case, the line crosses the \(y\)-axis at the constant \(b\). The number \(b\) is the number at which the line crosses the \(y\)-axis, and it is called the \(y\)-intercept. The ordered pair corresponding to the \(y\)-intercept is \((0, b)\).
Place your pencil at any point on the line. Move your pencil exactly one unit horizontally to the right. Now, how many units straight up or down must you move your pencil to get back on the line? Do you see this number in the equation?
- Answer
-
To get back on the line, we must move our pencil exactly \(m\) vertical units.
Slope
The number \(m\) is the coefficient of the variable \(x\). The number \(m\) is called the slope of the line and it is the number of units that \(y\) changes when \(x\) is increased by \(1\) unit. Thus, if \(x\) changes by \(1\) unit, \(y\) changes by \(m\) units.
Since the equation \(y=mx+b\) contains both the slope of the line and the \(y\)-intercept, we call the form \(y=mx+b\) the slope-intercept form.
The slope-intercept form of a straight line is \(y=mx+b\)
The slope of the line is \(m\), and the \(y\)-intercept is the point \((0 , b)\).
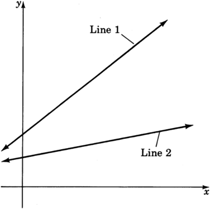
The Slope is a Measure of the Steepness of a Line
The word slope is really quite appropriate. It gives us a measure of the steepness of the line. Consider two lines, one with slope \(\dfrac{1}{2}\) and the other with slope \(3\). The line with slope \(3\) is steeper than is the line with slope \(\dfrac{1}{2}\). Imagine your pencil being placed at any point on the lines. We make a \(1\)-unit increase in the \(x\)-value by moving the pencil one unit to the right. To get back to one line we need only move vertically \(\dfrac{1}{2}\) unit, whereas to get back onto the other line we need to move vertically \(3\) units.
Sample Set C
Find the slope and the y-intercept of the following lines.
\(y = 2x + 7\)
The line is in the slope-intercept form \(y=mx+b\). The slope is \(m\), the coefficient of \(x\). Therefore, \(m=2\). The \(y\)-intercept is the point \((0, b)\). Since \(b=7\), the \(y\)-intercept is \((0, 7)\).
Slope:\(2\)
\(y\)-intercept: \((0, 7)\)
\(y = -4x + 1\)
The line is in the slope-intercept form \(y=mx+b\). The slope is \(m\), the coefficient of \(x\). Therefore, \(m=-4\). The \(y\)-intercept is the point \((0, b)\). Since \(b=1\), the \(y\)-intercept is \((0, 1)\).
Slope:\(-4\)
\(y\)-intercept: \((0, 1)\)
\(3x + 2y = 5\).
This equation is written in general form. We can put the equation in slope-intercept form by solving for \(y\).
\(\begin{aligned}
3x+2y&=5\\
2y&=-3x+5\\
y&=-\dfrac{3}{2}x + \dfrac{5}{2}
\end{aligned}\)
Now the equation is in slope-intercept form.
Slope:\(-\dfrac{3}{2}\)
\(y\)-intercept: \((0, \dfrac{5}{2})\)
Practice Set C
Find the slope and \(y\)-intercept of the line \(2x+5y=15\).
- Answer
-
Solving for \(y\) we get \(y = \dfrac{-2}{5}x + 3\). Now \(m = \dfrac{-2}{5}\) and \(b = 3\).
The Formula for the Slope of a Line
We have observed that the slope is a measure of the steepness of a line. We wish to develop a formula for measuring this steepness.
It seems reasonable to develop a slope formula that produces the following results:
Steepness of line \(1>\) steepness of line 2.
Consider a line on which we select any two points. We’ll denote these points with the ordered pairs \((x_1, y_1 )\) and \((x_2, y_2 )\). The subscripts help us to identify the points.
\((x_1, y_1)\) is the first point. Subscript \(1\) indicates the first point.
\((x_2, y_2)\) is the second point. Subscript \(2\) indicates the second point.
The difference in \(x\) values \((x_2−x_1)\) gives us the horizontal change, and the difference in \(y\) values \((y_2−y_1)\) gives us the vertical change. If the line is very steep, then when going from the first point to the second point, we would expect a large vertical change compared to the horizontal change. If the line is not very steep, then when going from the first point to the second point, we would expect a small vertical change compared to the horizontal change.
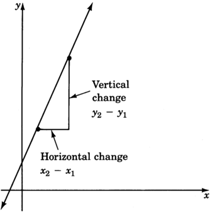
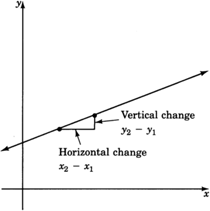
We are comparing changes. We see that we are comparing:
\(\begin{aligned}
\text{The vertical change}&\text{ to }&\text{ the horizontal change}\\
\text{The change in }y&\text{ to }&\text{ the change in }x\\
y_1-y_1&\text{ to }&x_2-x_1
\end{aligned}\)
This is a comparison and is therefore a ratio. Ratios can be expressed as fractions. Thus, a measure of the steepness of a line can be expressed as a ratio.
The slope of a line is defined as the ratio
\(\text{Slope } = \dfrac{\text{ change in } y}{\text{ change in } x}\)
Mathematically, we can write these changes as
\(\text{Slope } = \dfrac{y_2-y_1}{x_2-x_1}\)
The slope of a nonvertical line passing through the points \((x_1, y_1)\) and \((x_2, y_2)\) is found by the formula:
\(m = \dfrac{y_2 - y_1}{x_2 - x_1}\)
Sample Set D
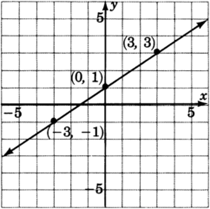
For the two given points, find the slope of the line that passes through them.
\((0,1)\) and \((1,3)\).
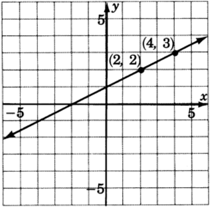
Looking left to right on the line we can choose \((x_1, y_1)\) to be \((0,1)\), and \((x_2, y_2)\) to be \((1, 3)\). Then,
\(m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{3-1}{1-0} = \dfrac{2}{1} = 2\)
This line has slope \(2\). It appears fairly steep. When the slope is written in fraction form, \(2 = \dfrac{2}{1}\), we can see, by recalling the slope formula, that as \(x\) changes \(1\) unit to the right (because of the \(+1\)) \(y\) changes \(2\) units upward (because of the \(+2\).
\(m = \dfrac{\text{ change in } y}{\text{ change in } x} = \dfrac{2}{1}\).
Notice that as we look left to right, the line rises.
\((2,2)\) and \((4,3)\).
Looking left to right on the line we can choose \((x_1, y_1)\) to be \((2,2)\), and \((x_2, y_2)\) to be \((4, 3)\). Then,
\(m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{3-2}{4-2} = \dfrac{1}{2}\)
This line has slope \(\dfrac{1}{2}\). Thus, as \(x\) changes \(2\) units to the right (because of the \(+2\), \(y\) changes \(1\) unit upward (because of the \(+1\)).
\(m = \dfrac{\text{ change in } y}{\text{ change in } x} = \dfrac{1}{2}\).
Notice that in examples 16 and 17, both lines have positive slopes, \(+2\) and \(+\dfrac{1}{2}\), and both lines rise as we look left to right.
\((-2, 4)\) and \((1,1)\).
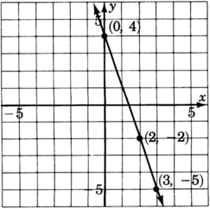
Looking left to right on the line we can choose \((x_1, y_1)\) to be \((-2,4)\), and \((x_2, y_2)\) to be \((1,1)\). Then,
\(m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{1-4}{1-(-2)} = \dfrac{-3}{1 + 2} = \dfrac{-3}{3} = -1\)
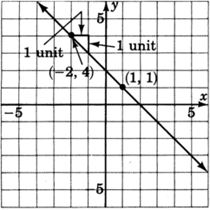
This line has slope \(-1\).
When the slope is written in fraction form, \(m = -1 = \dfrac{-1}{+1}\), we can see that as \(x\) changes \(1\) unit to the right (because of the \(+1\), \(y\) changes \(1\) unit downward (because of the \(-1\)).
Notice also that this line has a negative slope and declines as we look left to right.
\((1, 3)\) and \((5, 3)\).
\(m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{3-3}{5-1} = \dfrac{0}{4} = 0\)
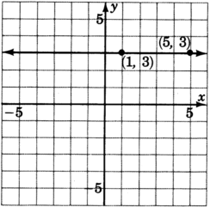
This line has \(0\) slope. This means it has no rise and, therefore, is a horizontal line. This does not mean that the line has no slope, however.
\((4,4)\) and \((4,0)\).
\(m = \dfrac{y_2-y_1}{x_2-x_1} = \dfrac{0-4}{4-4} = \dfrac{-4}{0}\)
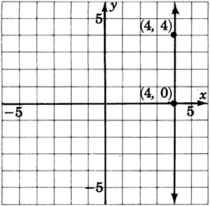
Since division by \(0\) is undefined, we say that vertical lines have undefined slope. Since there is no real number to represent the slope of this line, we sometimes say that vertical lines have undefined slope, or no slope.
Practice Set D
Find the slope of the line passing through \((2,1)\) and \((6,3)\). Graph this line on the graph of problem 2 below.
- Answer
-
\(m = \dfrac{3-1}{6-2} = \dfrac{2}{4} = \dfrac{1}{2}\)
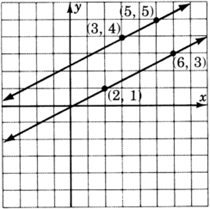
Find the slope of the line passing through \((3,4)\) and \((5,5)\). Graph this line.
- Answer
-
The line has slope \(\dfrac{1}{2}\)
Compare the lines of the following problems. Do the lines appear to cross? What is it called when lines do not meet (parallel or intersecting)? Compare their slopes. Make a statement about the condition of these lines and their slopes.
- Answer
-
The lines appear to be parallel. Parallel lines have the same slope, and lines that have the same slope are parallel
Before trying some problems, let’s summarize what we have observed.
- The equation \(y=mx+b\) is called the slope-intercept form of the equation of a line. The number \(m\) is the slope of the line and the point \((0,b)\) is the \(y\)-intercept.
- The slope, \(m\), of a line is defined as the steepness of the line, and it is the number of units that \(y\) changes when \(x\) changes \(1\) unit.
- The formula for finding the slope of a line through any two given points \((x_1,y_1)\) and \((x_2,y_2)\) is:
- \(m = \dfrac{y_2-y_1}{x_2-x_1}\)
- The fraction \(\dfrac{y_2-y_1}{x_2-x_1}\) represents the \dfrac{\text{ change in } y}{\text{ change in } x}
- As we look at a graph from left to right, lines with positive slope rise and lines with negative slope decline.
- Parallel lines have the same slope.
- Horizontal lines have 0 slope.
- Vertical lines have undefined slope (or no slope).
Exercises
For the following problems, determine the slope and y-intercept of the lines.
\(y=3x+4\)
- Answer
-
slope = \(3\); \(y\)-intercept= \((0,4)\)
\(y=2x+9\)
\(y=9x+1\)
- Answer
-
slope = \(9\); \(y\)-intercept= \((0,1)\)
\(y=7x+10\)
\(y=−4x+5\)
- Answer
-
slope = \(-4\); \(y\)-intercept= \((0,5)\)
\(y=−2x+8\)
\(y=−6x−1\)
- Answer
-
slope = \(-6\); \(y\)-intercept= \((0,-1)\)
\(y=−x−6\)
\(y=−x+2\)
- Answer
-
slope = \(-1\); \(y\)-intercept= \((0,2)\)
\(2y=4x+8\)
\(4y=16x+20\)
- Answer
-
slope = \(4\); \(y\)-intercept= \((0,5)\)
\(−5y=15x+55\)
\(−3y=12x−27\)
- Answer
-
slope = \(-4\); \(y\)-intercept= \((0,9)\)
\(y = \dfrac{3}{5} - 8\)
\(y = \dfrac{2}{7} - 12\)
- Answer
-
slope = \(\dfrac{2}{7}\); \(y\)-intercept= \((0,-12)\)
\(y = \dfrac{-1}{8}x + \dfrac{2}{3}\)
\(y = \dfrac{-4}{5} - \dfrac{4}{7}\)
- Answer
-
slope = \(-\dfrac{4}{5}\); \(y\)-intercept= \((0,-\dfrac{4}{7})\)
\(−3y=5x+8\)
\(−10y=−12x+1\)
- Answer
-
slope = \(\dfrac{6}{5}\); \(y\)-intercept= \((0,-\dfrac{1}{10})\)
\(−y=x+1\)
\(−y=−x+3\)
- Answer
-
slope = \(1\); \(y\)-intercept= \((0,-3)\)
\(3x−y=7\)
\(5x+3y=6\)
- Answer
-
slope = \(-\dfrac{5}{3}\); \(y\)-intercept= \((0,2)\)
\(−6x−7y=−12\)
\(−x+4y=−1\)
- Answer
-
slope = \(\dfrac{1}{4}\); \(y\)-intercept= \((0,-\dfrac{1}{4})\)
For the following problems, find the slope of the line through the pairs of points.
\((1, 6), (4,9)\)
\((1, 3), (4,7)\)
- Answer
-
\(m = \dfrac{4}{3}\)
\((3, 5), (4,7)\)
\((6, 1), (2,8)\)
- Answer
-
\(m = -\dfrac{7}{4}\)
\((0, 5), (2,−6)\)
\((−2, 1), (0,5)\)
- Answer
-
\(m=2\)
\((3, −9), (5,1)\)
\((4, −6), (−2,1)\)
- Answer
-
\(m = -\dfrac{7}{6}\)
\((−5, 4), (−1,0)\)
\((−3, 2), (−4,6)\)
- Answer
-
\(m=−4\)
\((9, 12), (6,0)\)
\((0, 0), (6,6)\)
- Answer
-
\(m=1\)
\((−2, −6), (−4,−1)\)
\((−1, −7), (−2,−9)\)
- Answer
-
\(m=2\)
\((−6, −6), (−5,−4)\)
\((−1, 0), (−2,−2)\)
- Answer
-
\(m=2\)
\((−4, −2), (0,0)\)
\((2, 3), (10,3)\)
- Answer
-
\(m=0\) (horizontal line \(y=3\))
Make a statement about the slopes of parallel lines.
\((4, −2), (4,7)\)
\((8, −1), (8,3)\)
- Answer
-
No slope (vertical line at \(x=8\))
\((4, 2), (6,2)\)
\((5, −6), (9,−6)\)
- Answer
-
\(m=0\) (horizontal line at \(y=−6\))
Do lines with a positive slope rise or decline as we look left to right?
Do lines with a negative slope rise or decline as we look left to right?
- Answer
-
decline
For the following problems, determine the slope and y-intercept of the lines. Round to two decimal places.
\(3.8x+12.1y=4.26\)
- Answer
-
slope=\(−0.31\)
\(y\)−intercept=\((0,0.35)\)
\(8.09x+5.57y=−1.42\)
\(10.813x−17.0y=−45.99\)
- Answer
-
slope=\(0.64\)
\(y\)−intercept=\((0,2.71)\)
\(−6.003x−92.388y=0.008\)
For the following problems, find the slope of the line through the pairs of points. Round to two decimal places.
\((5.56, 9.37), (2.16, 4.90)\)
- Answer
-
\(m=1.31\)
\((33.1, 8.9), (42.7, −1.06)\)
\((155.89, 227.61), (157.04,227.61)\)
- Answer
-
\(m=0\) (horizontal line at \(y=227.61\))
\((0.00426, −0.00404), (−0.00191, −0.00404)\)
\((88.81, −23.19), (88.81, −26.87)\)
- Answer
-
No slope (vertical line \(x=88.81\))
\((−0.0000567, −0.0000567), (−0.00765, 0.00764)\)
Exercises for Review
Simplify \((x^2y^3w^4)^0\).
- Answer
-
\(1\) if \(xyw≠0\)
Solve the equation \(3x−4(2−x)−3(x−2)+4=0\).
When four times a number is divided by five, and that result is decreased by eight, the result is zero. What is the original number?
- Answer
-
\(10\)
Solve \(−3y+10=x+2\) if \(x=−4\).
Graph the linear equation \(x+y=3\).
- Answer
-
