10.11: Proficiency Exam
- Page ID
- 60076
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Proficiency Exam
For the quadratic equations in the following problems, specify the values of \(a, b\), and \(c\).
\(2y^2 - 3y + 10 = 0\)
- Answer
-
\(a=2,b=−3,c=10\)
\(10b^2 = 3b\)
- Answer
-
\(a=10,b=−3,c=0\)
For the following problems, use the zero-factor property to solve each quadratic equation.
\((3x+5)(x−1)=0\)
- Answer
-
\(x = -\dfrac{5}{3}, 1\)
\(3b(2b−1)=0\)
- Answer
-
\(b = 0, \dfrac{1}{2}\)
\((a - 8)^2 = 0\)
- Answer
-
\(a=8\)
For the following problems, solve each quadratic equation by factoring.
\(4x^2 - 16 = 0\)
- Answer
-
\(x=−2,2\)
\(y^2 - 12y + 32 = 0\)
- Answer
-
\(y=4,8\)
\(a^2 - 5a = 14\)
- Answer
-
\(−2,7\)
\(6a^2 = 10 - 11a\)
- Answer
-
\(a = -\dfrac{5}{2}, \dfrac{2}{3}\)
\(2x^2 = -2 - 5x\)
- Answer
-
\(x = -2, -\dfrac{1}{2}\)
\(x^3 - 25x = 0\)
- Answer
-
\(x=0,−5,5\)
For the following problems, solve each quadratic equation by extraction of roots.
\(c^2 = 81\)
- Answer
-
\(c=−9,9\)
\(x^2 = 15\)
- Answer
-
\(x = -\sqrt{15}, \sqrt{15}\)
\(3a^2 - 18 = 0\)
- Answer
-
\(a = -\sqrt{6}, \sqrt{6}\)
\((x - 5)^2 = 1\)
- Answer
-
\(x=4,6\)
\((y + 11)^2 - 9 = 0\)
- Answer
-
\(y=−8,−14\)
\(y^2 - 25z^2 = 0\) for \(y\).
- Answer
-
\(y=−5z,5z\)
\(6a^2 - 18b^2c^2\) for \(a\)
- Answer
-
\(a = \pm bc\sqrt{3}\)
For the following problems, solve each quadratic equation using the quadratic formula.
\(x^2 - 6x - 16 = 0\)
- Answer
-
\(x=−2,8\)
\(y^2 - 2y - 7 = 0\)
- Answer
-
\(y = 1 + 2\sqrt{2}\)
\((m + 2)^2 - 5 = 0\)
- Answer
-
\(m = -2 \pm \sqrt{5}\)
\((x + b)^2 = c^2\)
- Answer
-
\(x = -b \pm c\)
\((x+1)(x+4)=6\)
- Answer
-
\(x = \dfrac{-5 \pm \sqrt{33}}{2}\)
\(5z^2 - 5z - 5 = 2z^2 - z\)
- Answer
-
\(z = \dfrac{2 \pm \sqrt{19}}{3}\)
\(2m^2 = 5m\)
- Answer
-
\(m = 0, \dfrac{5}{2}\)
For the following problems, solve each quadratic equation by completing the square.
\(x^2 + 6x - 8 = 0\)
- Answer
-
\(x = -3 \pm \sqrt{17}\)
\(2x^2 + 7x - 12 = 0\)
- Answer
-
\(x = \dfrac{-7 \pm \sqrt{145}}{4}\)
The product of two consecutive odd integers is 143. What are they?
- Answer
-
11 and 13 or −11 and −13
A study of the air quality by an environmental group suggests that t years from now the level of carbon monoxide in the air, in parts per million, will be given by the quadratic equation
\(A = 0.4t^2 + 0.1t + 3.1\)
where \(A\) represents the amount of carbon monoxide in the air.
a) What is the level, in parts per million, of carbon monoxide in the air now?
b) How many years from now will the level of carbon monoxide be at 18.1 parts per million?
- Answer
-
(a) 3.1
(b) 6 years from now
The length of a rectangle is 6 inches longer than the width of the rectangle. Find the dimensions of the rectangle if the area is 112 square feet.
- Answer
-
width: \(\dfrac{-1 + \sqrt{1793}}{4}\)
length: \(\dfrac{1 + \sqrt{1793}}{4}\)
For the following problems, construct the graphs of the following equations.
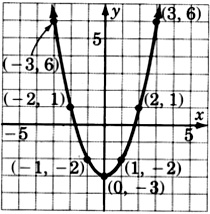
\(y = x^2 - 3\)
- Answer
-
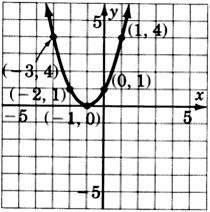
\(y = (x + 1)^2\)
- Answer
-
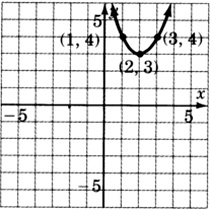
\(y = (x-2)^2 + 3\)
- Answer
-
For the following problems, write the equation that corresponds to each graph.
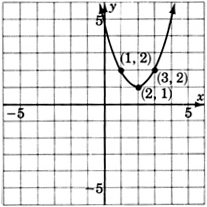
- Answer
-
\(y = (x-2)^2 + 1\) or \(y = x^2 - 4x + 5\)
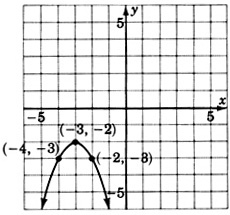
- Answer
-
\(y = -(x + 3)^2 - 2\) or \(y = -x^2 - 6x - 11\)