4.7: Graphs of Linear Inequalities

Last updated
Save as PDF

Page ID: 15149

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

By the end of this section, you will be able to:

Verify solutions to an inequality in two variables
Recognize the relation between the solutions of an inequality and its graph
Graph linear inequalities

Note

Before you get started, take this readiness quiz.

Solve: $4x+3>23.$
If you missed this problem, review Exercise 2.7.22.
Translate from algebra to English: $x<5.$
If you missed this problem, review Exercise 1.3.1.
Evaluate $3x−2y$ when $x=1, \, y=−2.$
If you missed this problem, review Exercise 1.5.28.

Verify Solutions to an Inequality in Two Variables

We have learned how to solve inequalities in one variable. Now, we will look at inequalities in two variables. Inequalities in two variables have many applications. If you ran a business, for example, you would want your revenue to be greater than your costs—so that your business would make a profit.

LINEAR INEQUALITY

A linear inequality is an inequality that can be written in one of the following forms:

\[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C \nonumber\]

where $A$ and $B$ are not both zero.

Do you remember that an inequality with one variable had many solutions? The solution to the inequality $x>3$ is any number greater than $3$. We showed this on the number line by shading in the number line to the right of $3$, and putting an open parenthesis at $3$. See Figure $\PageIndex{1}$.

The figure shows a number line extending from negative 5 to 5. A parenthesis is shown at positive 3 and an arrow extends form positive 3 to positive infinity. — Figure $\PageIndex{1}$

Similarly, inequalities in two variables have many solutions. Any ordered pair $ (x, y)$ that makes the inequality true when we substitute in the values is a solution of the inequality.

Solution OF A LINEAR INEQUALITY

An ordered pair $ (x, y)$ is a solution of a linear inequality if the inequality is true when we substitute the values of $x$ and $y$.

Example $\PageIndex{1}$

Determine whether each ordered pair is a solution to the inequality $y>x+4$:

$(0,0)$
$(1,6)$
$(2,6)$
$(−5,−15)$
$(−8,12)$

Solution

$(0,0)$		$.$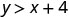
$.$		$.$
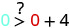Simplify.		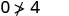$.$ So, $(0,0)$ is not a solution to $y>x+4$.

$(1,6)$		$.$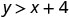
$.$		$.$
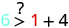Simplify.		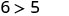$.$ So, $(1,6)$ is a solution to $y>x+4$.

$(2,6)$		$.$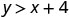
$.$		$.$
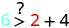Simplify.		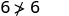$.$ So, $(2,6)$ is not a solution to $y>x+4$.

$(−5,−15)$		$.$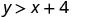
$.$		$.$
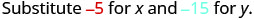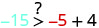Simplify.		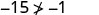$.$ So, $(−5,−15)$ is not a solution to $y>x+4$.

(−8,12)		$.$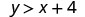
$.$		$.$
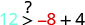Simplify.		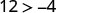$.$ So, $(−8,12)$ is a solution to $y>x+4$.

Try It $\PageIndex{2}$

Determine whether each ordered pair is a solution to the inequality $y>x−3$:

$(0,0)$
$(4,9)$
$(−2,1)$
$(−5,−3)$
$(5,1)$

Answer

Try It $\PageIndex{3}$

Determine whether each ordered pair is a solution to the inequality $y<x+1$:

$(0,0)$
$(8,6)$
$(−2,−1)$
$(3,4)$
$(−1,−4)$

Answer

Recognize the Relation Between the Solutions of an Inequality and its Graph

Now, we will look at how the solutions of an inequality relate to its graph.

Let’s think about the number line in Figure $\PageIndex{1}$ again. The point $x=3$ separated that number line into two parts. On one side of $3$ are all the numbers less than $3$. On the other side of $3$ all the numbers are greater than $3$. See Figure $\PageIndex{2}$.

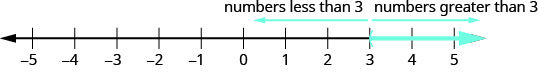
The solution to $x>3$ is the shaded part of the number line to the right of $x=3$.

Similarly, the line $y=x+4$ separates the plane into two regions. On one side of the line are points with $y<x+4$. On the other side of the line are the points with $y>x+4$. We call the line $y=x+4$ a boundary line.

BOUNDARY LINE

The line with equation $Ax+By=C$ is the boundary line that separates the region where $Ax+By>C$ from the region where $Ax+By<C$.

For an inequality in one variable, the endpoint is shown with a parenthesis or a bracket depending on whether or not aa is included in the solution:

$The figure shows two number lines. The number line on the left is labeled x is less than a. The number line shows a parenthesis at a and an arrow that points to the left. The number line on the right is labeled x is less than or equal to a. The number line shows a bracket at a and an arrow that points to the left.$

Similarly, for an inequality in two variables, the boundary line is shown with a solid or dashed line to indicate whether or not it the line is included in the solution. This is summarized in Table $\PageIndex{1}$.

Table $\PageIndex{1}$
$Ax+By<C$	$Ax+By\leq C$
$Ax+By>C$	$Ax+By\geq C$
Boundary line is not included in solution.	Boundary line is included in solution.
Boundary line is dashed.	Boundary line is solid.

Now, let’s take a look at what we found in Example $\PageIndex{1}$. We’ll start by graphing the line $y=x+4$, and then we’ll plot the five points we tested. See Figure $\PageIndex{3}$.

The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The line y equals x plus 4 is plotted as an arrow extending from the bottom left toward the upper right. The following points are plotted and labeled (negative 8, 12), (1, 6), (2, 6), (0, 0), and (negative 5, negative 15). — Figure $\PageIndex{3}$

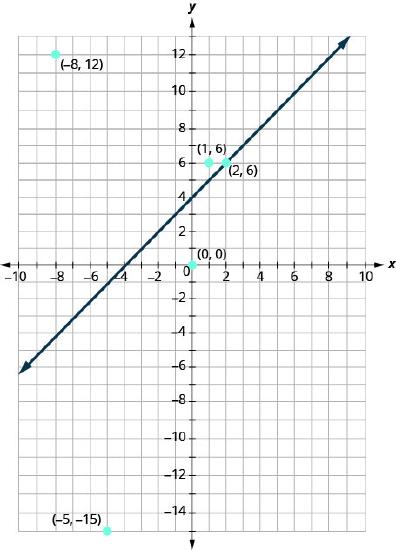
In Example $\PageIndex{1}$ we found that some of the points were solutions to the inequality $y>x+4$ and some were not.

Which of the points we plotted are solutions to the inequality $y>x+4$? The points $(1,6)$ and $(−8,12)$ are solutions to the inequality $y>x+4$. Notice that they are both on the same side of the boundary line $y=x+4$.

The two points $(0,0)$ and $(−5,−15)$ are on the other side of the boundary line $y=x+4$, and they are not solutions to the inequality $y>x+4$. For those two points, $y<x+4$.

What about the point $(2,6)$? Because $6=2+4$, the point is a solution to the equation $y=x+4$. So the point $(2,6)$ is on the boundary line.

Let’s take another point on the left side of the boundary line and test whether or not it is a solution to the inequality $y>x+4$. The point $(0,10)$ clearly looks to be to the left of the boundary line, doesn’t it? Is it a solution to the inequality?

\[\begin{array}{l}{y>x+4} \\ {10\stackrel{?}{>}0+4} \\ {10>4} &{\text{So, }(0,10)\text{ is a solution to }y>x+4.}\end{array}\]

Any point you choose on the left side of the boundary line is a solution to the inequality $y>x+4$. All points on the left are solutions.

Similarly, all points on the right side of the boundary line, the side with $(0,0)$ and $(−5,−15)$, are not solutions to $y>x+4$. See Figure $\PageIndex{4}$.

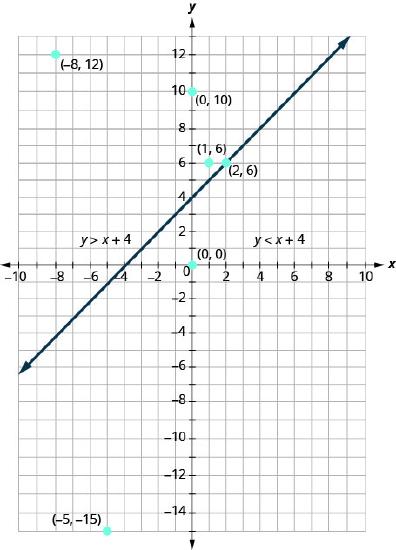
The graph of the inequality $y>x+4$ is shown in Figure $\PageIndex{5}$ below. The line $y=x+4$ divides the plane into two regions. The shaded side shows the solutions to the inequality $y>x+4$.

The points on the boundary line, those where $y=x+4$, are not solutions to the inequality $y>x+4$, so the line itself is not part of the solution. We show that by making the line dashed, not solid.

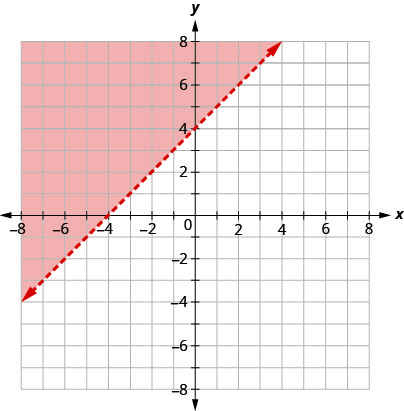
The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The line y equals x plus 4 is plotted as a dashed arrow extending from the bottom left toward the upper right. The coordinate plane to the upper left of the line is shaded. — Figure $\PageIndex{5}$: The graph of the inequality y>x+4.

Example $\PageIndex{4}$

The boundary line shown is $y=2x−1$. Write the inequality shown by the graph.

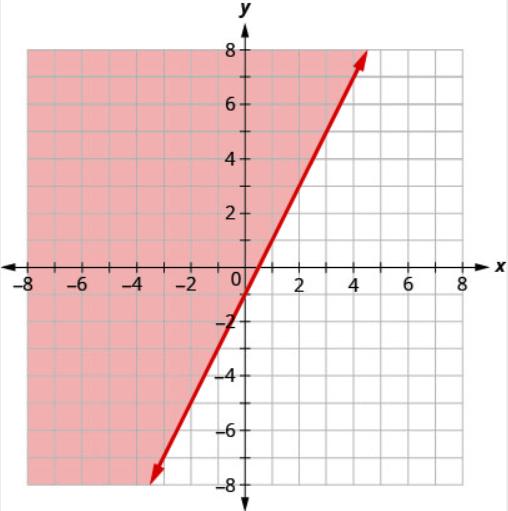
$example 4.7.4.png and y-axes each run from negative 10 to 10. The line y equals 2 x minus 1 is plotted as a solid arrow extending from the bottom left toward the upper right. The coordinate plane to the left of the line is shaded$

Solution

The line $y=2x−1$ is the boundary line. On one side of the line are the points with $y>2x−1$ and on the other side of the line are the points with $y<2x−1$.

Let’s test the point $(0,0)$ and see which inequality describes its side of the boundary line.

At $(0,0)$, which inequality is true:

\[\begin{array}{ll}{y>2 x-1} & {\text { or }} & {y<2 x-1 ?} \\ {y>2 x-1} && {y<2 x-1} \\ {0>2 \cdot 0-1} && {0<2 \cdot 0-1} \\ {0>-1 \text { True }} && {0<-1 \text { False }}\end{array}\]

Since $y>2x−1$ is true, the side of the line with $(0,0)$, is the solution. The shaded region shows the solution of the inequality $y>2x−1$.

Since the boundary line is graphed with a solid line, the inequality includes the equal sign.

The graph shows the inequality $y\geq 2x−1$.

We could use any point as a test point, provided it is not on the line. Why did we choose $(0,0)$? Because it’s the easiest to evaluate. You may want to pick a point on the other side of the boundary line and check that $y<2x−1$.

Try It $\PageIndex{5}$

Write the inequality shown by the graph with the boundary line $y=−2x+3$.

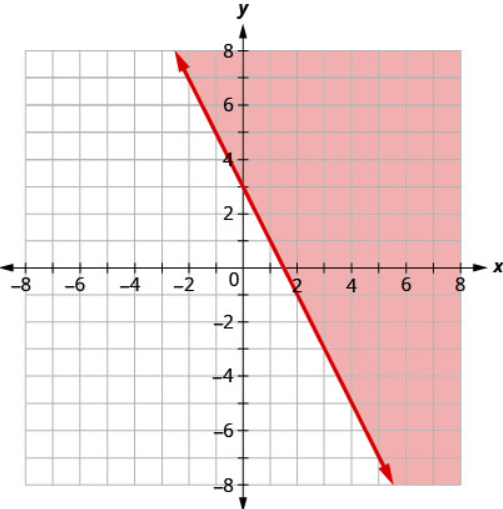
$example 4.7.5.png and y-axes each run from negative 10 to 10. The line y equals negative 2 x plus 3 is plotted as a solid arrow extending from the top left toward the bottom right. The coordinate plane to the right of the line is shaded.$

Answer: $y\geq −2x+3$

Try It $\PageIndex{6}$

Write the inequality shown by the graph with the boundary line $y=\frac{1}{2}x−4$.

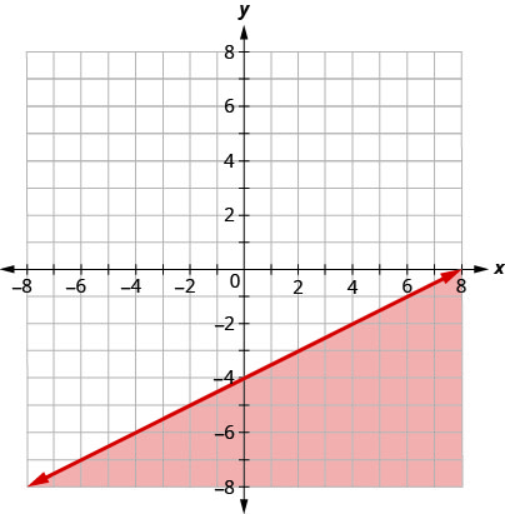
$example 4.7.6.png x and y-axes each run from negative 10 to 10. The line y equals one half x minus 4 is plotted as a solid arrow extending from the bottom left toward the top right. The coordinate plane to the bottom right of the line is shaded.$

Answer: $y \leq \frac{1}{2}x - 4$

Example $\PageIndex{7}$

The boundary line shown is $2x+3y=6$. Write the inequality shown by the graph.

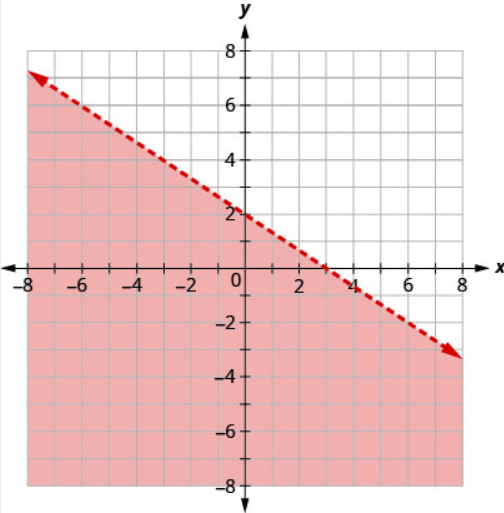
$example 4.7.7.png x and y-axes each run from negative 10 to 10. The line 2 x plus 3 y equals 6 is plotted as a dashed arrow extending from the top left toward the bottom right. The coordinate plane to the bottom of the line is shaded.$

Solution

The line $2x+3y=6$ is the boundary line. On one side of the line are the points with $2x+3y>6$ and on the other side of the line are the points with $2x+3y<6$.

Let’s test the point $(0,0)$ and see which inequality describes its side of the boundary line.

At $(0,0)$, which inequality is true:

\[\begin{array}{rr}{2 x+3 y>6} && {\text { or } \quad 2 x+3 y<6 ?} \\ {2 x+3 y>6} && {2 x+3 y<6} \\ {2(0)+3(0)>6} & & {2(0)+3(0)<6} \\ {0} >6 & {\text { False }} & {0<6}&{ \text { True }}\end{array}\]

So the side with $(0,0)$ is the side where $2x+3y<6$.

(You may want to pick a point on the other side of the boundary line and check that $2x+3y>6$.)

Since the boundary line is graphed as a dashed line, the inequality does not include an equal sign.

The graph shows the solution to the inequality $2x+3y<6$.

Try It $\PageIndex{8}$

Write the inequality shown by the shaded region in the graph with the boundary line $x−4y=8$.

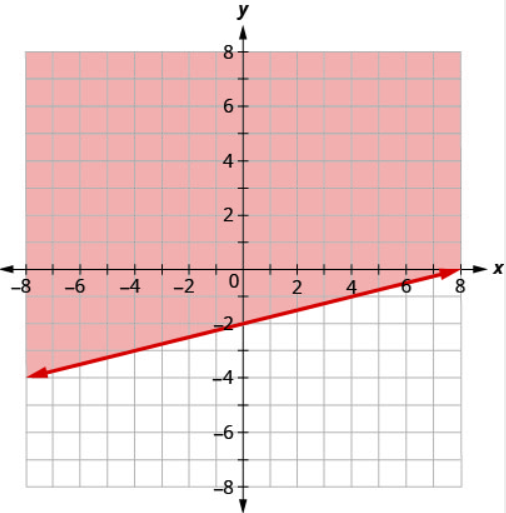
$example 4.7.8.png x and y-axes each run from negative 10 to 10. The line x minus 4 y equals 8 is plotted as a solid arrow extending from the bottom left toward the top right. The coordinate plane to the top of the line is shaded.$

Answer: $x-4 y \leq 8$

Try It $\PageIndex{9}$

Write the inequality shown by the shaded region in the graph with the boundary line $3x−y=6$.

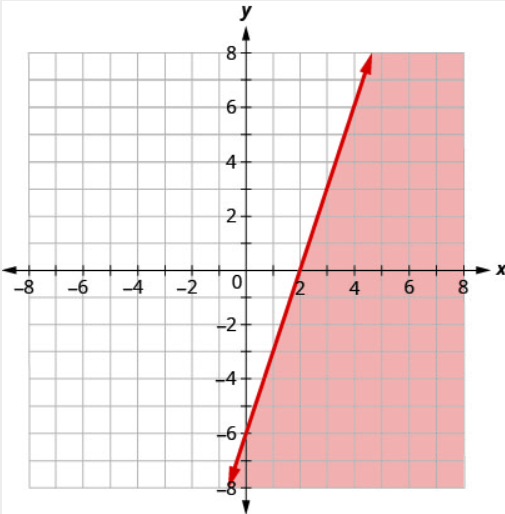
$example 4.7.9.pngx and y-axes each run from negative 10 to 10. The line 3 x minus y equals 6 is plotted as a solid arrow extending from the bottom left toward the top right. The coordinate plane to the right of the line is shaded.$

Answer: $3 x-y \leq 6$

Graph Linear Inequalities

Now, we’re ready to put all this together to graph linear inequalities.

Example $\PageIndex{10}$: How to Graph Linear Inequalities

Graph the linear inequality $y \geq \frac{3}{4} x-2$.

Solution

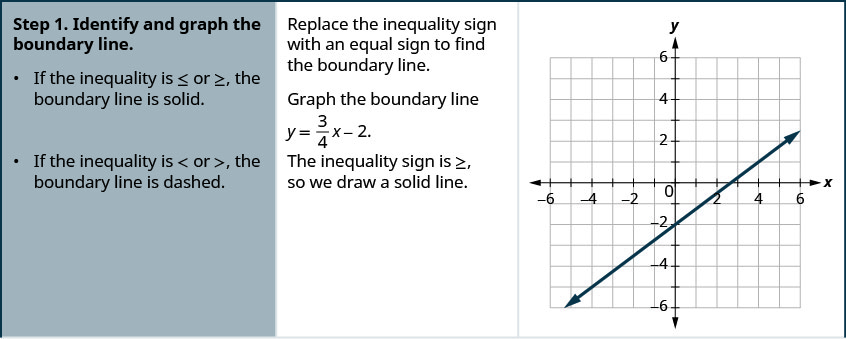
$This figure is a table that has three columns and three rows. The first column is a header column, and it contains the names and numbers of each step. The second column contains further written instructions. The third column contains math. On the top row of the table, the first cell on the left reads: “Step 1. Identify and graph the boundary line. If the inequality is less than or equal to or greater than or equal to, the boundary line is solid. If the inequality is less than or greater than, the boundary line is dashed. The text in the second cell reads: “Replace the inequality sign with an equal sign to find the boundary line. Graph the boundary line y equals three-fourths x minus 2. The inequality sign is greater than or equal to, so we draw a solid line. The third cell contains the graph of the line three-fourths x minus 2 on a coordinate plane.$ $In the second row of the table, the first cell says: “Step 2. Test a point that is not on the boundary line. Is it a solution of the inequality? In the second cell, the instructions say: “We’ll test (0, 0). Is it a solution of the inequality?” The third cell asks: At (0, 0), is y greater than or equal to three-fourths x minus 2? Below that is the inequality 0 is greater than or equal to three-fourths 0 minus 2, with a question mark above the inequality symbol. Below that is the inequality 0 is greater than or equal to negative 2. 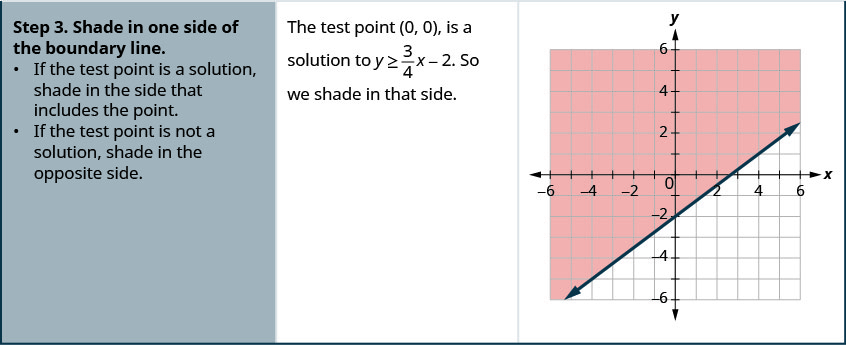Below that is: “So (0, 0) is a solution.$ $In the third row of the table, the first cell says: “Step 3. Shade in one side of the boundary line. If the test point is a solution, shade in the side that includes the point. If the test point is not a solution, shade in the opposite side. In the second cell, the instructions say: The test point (0, 0) is a solution to y is greater than or equal to three-fourths x minus 2. So we shade in that side.” In the third cell is the graph of the line three-fourths x minus 2 on a coordinate plane with the region above the line shaded.$

Try It $\PageIndex{11}$

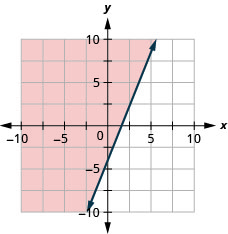
Graph the linear inequality $y \geq \frac{5}{2} x-4$.

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The line y equals five-halves x minus 4 is plotted as a solid arrow extending from the bottom left toward the top right. The region above the line is shaded.$

Try It $\PageIndex{12}$

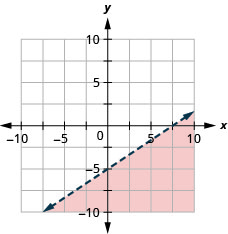
Graph the linear inequality $y<\frac{2}{3} x-5$.

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The line y equals two-thirds x minus 5 is plotted as a dashed arrow extending from the bottom left toward the top right. The region below the line is shaded.$

The steps we take to graph a linear inequality are summarized here.

GRAPH A LINEAR INEQUALITY.

Identify and graph the boundary line.
- If the inequality is $≤$ or $≥$, the boundary line is solid.
- If the inequality is $<$ or $>$, the boundary line is dashed.
Test a point that is not on the boundary line. Is it a solution of the inequality?
Shade in one side of the boundary line.
- If the test point is a solution, shade in the side that includes the point.
- If the test point is not a solution, shade in the opposite side.

Example $\PageIndex{13}$

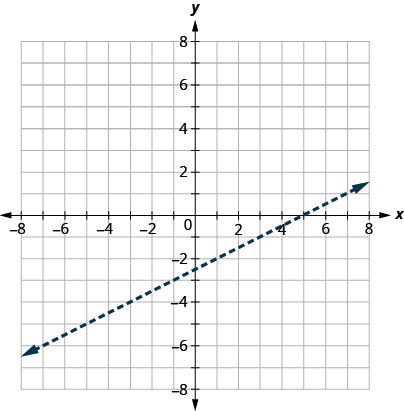
Graph the linear inequality $x−2y<5$.

Solution

First we graph the boundary line $x−2y=5$. The inequality is $<$ so we draw a dashed line.

$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The line x minus 2 y equals 5 is plotted as a dashed arrow extending from the bottom left toward the top right.$

Then we test a point. We’ll use $(0,0)$ again because it is easy to evaluate and it is not on the boundary line.

Is $(0,0)$ a solution of $x−2y<5$?

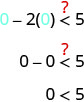
$The figure shows the inequality 0 minus 2 times 0 in parentheses is less than 5, with a question mark above the inequality symbol. The next line shows 0 minus 0 is less than 5, with a question mark above the inequality symbol. The third line shows 0 is less than 5.$

The point $(0,0)$ is a solution of $x−2y<5$, so we shade in that side of the boundary line.

Try It $\PageIndex{14}$

Graph the linear inequality $2x−3y\leq 6$.

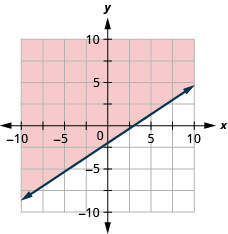
Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The line 2 x minus 3 y equals 6 is plotted as a solid arrow extending from the bottom left toward the top right. The region above the line is shaded.$

Try It $\PageIndex{15}$

Graph the linear inequality $2x−y>3$.

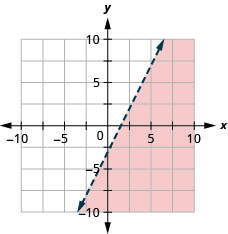
Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The line 2 x minus y equals 3 is plotted as a dashed arrow extending from the bottom left toward the top right. The region below the line is shaded.$

What if the boundary line goes through the origin? Then we won’t be able to use $(0,0)$ as a test point. No problem—we’ll just choose some other point that is not on the boundary line.

Example $\PageIndex{16}$

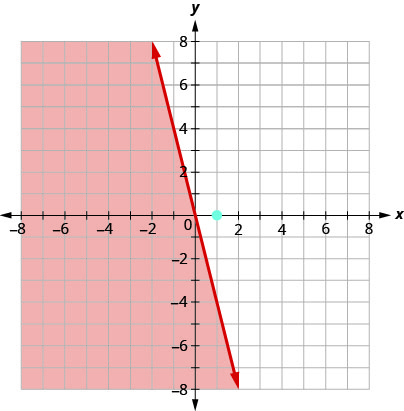
Graph the linear inequality $y\leq −4x$.

Solution

First we graph the boundary line $y=−4x$. It is in slope–intercept form, with $m=−4$ and $b=0$. The inequality is $≤$ so we draw a solid line.

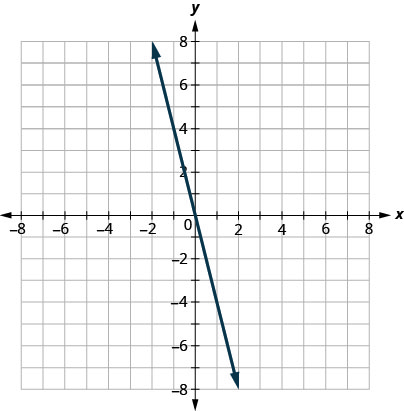
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The line s y equals negative 4 x is plotted as a solid arrow extending from the top left toward the bottom right.$

Now, we need a test point. We can see that the point $(1,0)$ is not on the boundary line.

Is $(1,0)$ a solution of $y≤−4x$?

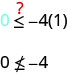
$The figure shows 0 is less than or equal to negative 4 times 1 in parentheses, with a question mark above the inequality symbol. The next line shows 0 is not less than or equal to negative 4.$

The point $(1,0)$ is not a solution to $y≤−4x$, so we shade in the opposite side of the boundary line. See Figure $\PageIndex{6}$.

The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The line y equals negative 4 x is plotted as a solid arrow extending from the top left toward the bottom right. The point (1, 0) is plotted, but not labeled. The region to the left of the line is shaded. — Figure $\PageIndex{6}$

Try It $\PageIndex{17}$

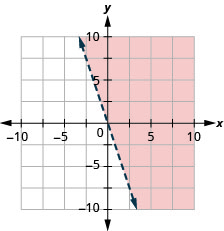
Graph the linear inequality $y>−3x$.

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The line y equals negative 3 x is plotted as a dashed arrow extending from the top left toward the bottom right. The region to the right of the line is shaded.$

Try It $\PageIndex{18}$

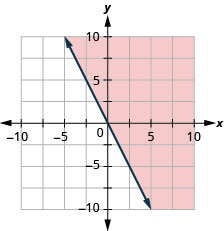
Graph the linear inequality $y\geq −2x$.

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The line y equals negative 2 x is plotted as a solid arrow extending from the top left toward the bottom right. The region to the right of the line is shaded.$

Some linear inequalities have only one variable. They may have an $x$ but no $y$, or a $y$ but no $x$. In these cases, the boundary line will be either a vertical or a horizontal line. Do you remember?

$\begin{array}{ll}{x=a} & {\text { vertical line }} \\ {y=b} & {\text { horizontal line }}\end{array}$

Example $\PageIndex{19}$

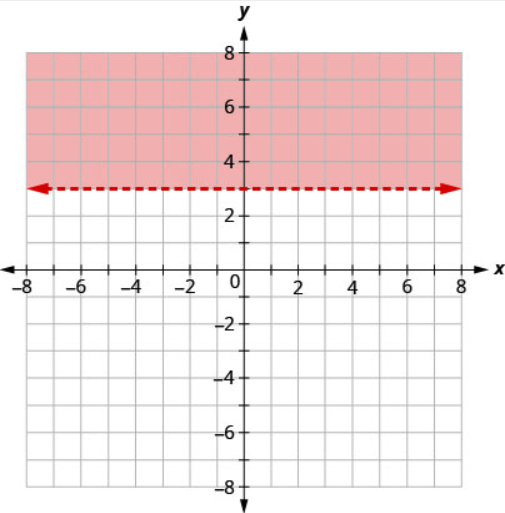
Graph the linear inequality $y>3$.

Solution

First we graph the boundary line $y=3$. It is a horizontal line. The inequality is $>$ so we draw a dashed line.

We test the point $(0,0)$.

\[y>3 \\ 0\not>3\]

$(0,0)$ is not a solution to $y>3$.

So we shade the side that does not include $(0,0)$.

$example 4.7.19.pngx and y-axes each run from negative 10 to 10. The line y equals 3 is plotted as a dashed arrow horizontally across the plane. The region above the line is shaded.$

Try It $\PageIndex{20}$

Graph the linear inequality $y<5$.

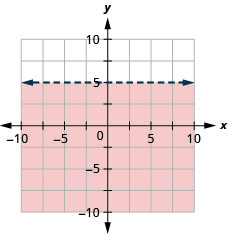
Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The line y equals 5 is plotted as a dashed arrow horizontally across the plane. The region above the line is shaded.$

Try It $\PageIndex{21}$

Graph the linear inequality $y \leq-1$.

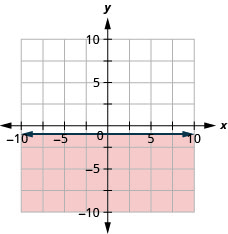
Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 10 to 10. The line y equals negative 1 is plotted as a dashed arrow horizontally across the plane. The region below the line is shaded.$

Key Concepts

To Graph a Linear Inequality
1. Identify and graph the boundary line.
  If the inequality is $≤$ or $≥$, the boundary line is solid.
  If the inequality is $<$ or $>$, the boundary line is dashed.
2. Test a point that is not on the boundary line. Is it a solution of the inequality?
3. Shade in one side of the boundary line.
  If the test point is a solution, shade in the side that includes the point.
  If the test point is not a solution, shade in the opposite side.

Glossary

boundary line: The line with equation $A x+B y=C$ that separates the region where $A x+B y>C$ from the region where $A x+B y<C$.

linear inequality: An inequality that can be written in one of the following forms:
\[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C\]
where $A$ and $B$ are not both zero.

solution of a linear inequality: An ordered pair $(x,\,y)$ is a solution to a linear inequality the inequality is true when we substitute the values of $x$ and $y$.

Search

Text Color

Text Size

Margin Size

Font Type

LINEAR INEQUALITY

Solution OF A LINEAR INEQUALITY

Example \(\PageIndex{1}\)

Try It \(\PageIndex{2}\)

Try It \(\PageIndex{3}\)

BOUNDARY LINE

Example \(\PageIndex{4}\)

Try It \(\PageIndex{5}\)

Try It \(\PageIndex{6}\)

Example \(\PageIndex{7}\)

Try It \(\PageIndex{8}\)

Try It \(\PageIndex{9}\)

Example \(\PageIndex{10}\): How to Graph Linear Inequalities

Try It \(\PageIndex{11}\)

Try It \(\PageIndex{12}\)

GRAPH A LINEAR INEQUALITY.

Example \(\PageIndex{13}\)

Try It \(\PageIndex{14}\)

Try It \(\PageIndex{15}\)

Example \(\PageIndex{16}\)

Try It \(\PageIndex{17}\)

Try It \(\PageIndex{18}\)

Example \(\PageIndex{19}\)

Try It \(\PageIndex{20}\)

Try It \(\PageIndex{21}\)

\((0,0)\)		$.$
$.$		$.$
Simplify.		$.$ So, \((0,0)\) is not a solution to \(y>x+4\).

\((1,6)\)		$.$
$.$		$.$
Simplify.		$.$ So, \((1,6)\) is a solution to \(y>x+4\).

\((2,6)\)		$.$
$.$		$.$
Simplify.		$.$ So, \((2,6)\) is not a solution to \(y>x+4\).

\((−5,−15)\)		$.$
$.$		$.$
Simplify.		$.$ So, \((−5,−15)\) is not a solution to \(y>x+4\).

(−8,12)		$.$
$.$		$.$
Simplify.		$.$ So, \((−8,12)\) is a solution to \(y>x+4\).

\(Ax+By<C\)	\(Ax+By\leq C\)
\(Ax+By>C\)	\(Ax+By\geq C\)
Boundary line is not included in solution.	Boundary line is included in solution.
Boundary line is dashed.	Boundary line is solid.