Chapter 4 Review Exercises

Last updated
Save as PDF

Page ID: 30235

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Chapter 4 Review Exercises

Rectangular Coordinate System

Plot Points in a Rectangular Coordinate System

In the following exercises, plot each point in a rectangular coordinate system.

Exercise $\PageIndex{1}$

(−1,−5)
(−3,4)
(2,−3)
$\left(1, \frac{5}{2}\right)$

Exercise $\PageIndex{2}$

(4,3)
(−4,3)
(−4,−3)
(4,−3)

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 6 to 6. The point (4, 3) is plotted and labeled "a". The point (negative 4, 3) is plotted and labeled "b". The point (negative 4, negative 3) is plotted and labeled "c". The point (4, negative 3) is plotted and labeled “d”.$

Exercise $\PageIndex{3}$

(−2,0)
(0,−4)
(0,5)
(3,0)

Exercise $\PageIndex{4}$

$\left(2, \frac{3}{2}\right)$
$\left(3, \frac{4}{3}\right)$
$\left(\frac{1}{3},-4\right)$
$\left(\frac{1}{2},-5\right)$

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 6 to 6. The point (2, three halves) is plotted and labeled "a". The point (3, four thirds) is plotted and labeled "b". The point (one third, negative 4) is plotted and labeled "c". The point (one-half, negative 5) is plotted and labeled “d”.$

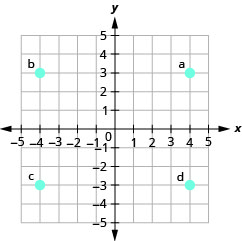
Identify Points on a Graph

In the following exercises, name the ordered pair of each point shown in the rectangular coordinate system.

Exercise $\PageIndex{5}$

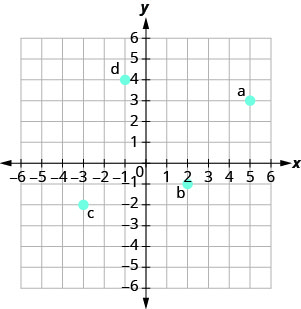
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 6 to 6. The point (5, 3) is plotted and labeled "a". The point (2, negative 1) is plotted and labeled "b". The point (negative 3, negative 2) is plotted and labeled "c". The point (negative 1, 4) is plotted and labeled “d”.$

Exercise $\PageIndex{6}$

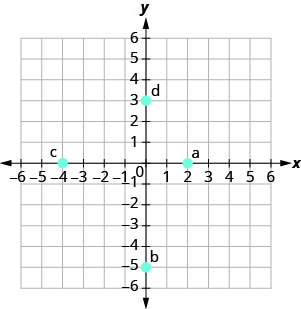
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 6 to 6. The point (2, 0) is plotted and labeled "a". The point (0, negative 5) is plotted and labeled "b". The point (negative 4, 0) is plotted and labeled "c". The point (0, 3) is plotted and labeled “d”.$

Answer

a. (2,0)

b (0,−5)

c (−4.0)

d (0,3)

Verify Solutions to an Equation in Two Variables

In the following exercises, which ordered pairs are solutions to the given equations?

Exercise $\PageIndex{7}$

$5x+y=10$

(5,1)
(2,0)
(4,−10)

Exercise $\PageIndex{8}$

$y=6x−2$

(1,4)
$\left(\frac{1}{3}, 0\right)$
(6,−2)

Answer: 1, 2

Complete a Table of Solutions to a Linear Equation in Two Variables

In the following exercises, complete the table to find solutions to each linear equation.

Exercise $\PageIndex{9}$

$y=4 x-1$

x	y	(x,y)
0
1
-2

Exercise $\PageIndex{10}$

$y=-\frac{1}{2} x+3$

x	y	(x,y)
0
4
-2

Answer

x	y	(x,y)
0	3	(0,3)
4	1	(4, 1)
−2	4	(−2,4)

Exercise $\PageIndex{11}$

$x+2 y=5$

x	y	(x,y)
	0
1
-1

Exercise $\PageIndex{12}$

$3x+2y=6$

x	y	(x,y)
0
	0
-2

Answer

x	y	(x,y)
0	−3	(0,−3)
2	0	(2,0)
−2	−6	(−2,−6)

Find Solutions to a Linear Equation in Two Variables

In the following exercises, find three solutions to each linear equation.

Exercise $\PageIndex{13}$

$x+y=3$

Exercise $\PageIndex{14}$

$x+y=-4$

Answer: Answers will vary.

Exercise $\PageIndex{15}$

$y=3 x+1$

Exercise $\PageIndex{16}$

$y=-x-1$

Answer: Answers will vary.

Graphing Linear Equations

Recognize the Relation Between the Solutions of an Equation and its Graph

In the following exercises, for each ordered pair, decide:

Is the ordered pair a solution to the equation?
Is the point on the line?

Exercise $\PageIndex{17}$

$y=−x+4$

(0,4) (−1,3)

(2,2) (−2,6)

$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals negative x plus 4 is plotted as an arrow extending from the top left toward the bottom right.$

Exercise $\PageIndex{18}$

$y=\frac{2}{3} x-1$
$(0,-1) (3,1)$
$(-3,-3) (6,4)$

$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals two-thirds x minus 1 is plotted as an arrow extending from the bottom left toward the top right.$

Answer

yes; yes
yes; no

Graph a Linear Equation by Plotting Points

In the following exercises, graph by plotting points.

Exercise $\PageIndex{19}$

$y=4x-3$

Exercise $\PageIndex{20}$

$y=-3x$

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals negative 3 x is plotted as an arrow extending from the top left toward the bottom right.$

Exercise $\PageIndex{21}$

$y=\frac{1}{2} x+3$

Exercise $\PageIndex{22}$

$x-y=6$

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line x minus y equals 6 is plotted as an arrow extending from the bottom left toward the top right.$

Exercise $\PageIndex{23}$

$2x+y=7$

Exercise $\PageIndex{24}$

$3x-2y=6$

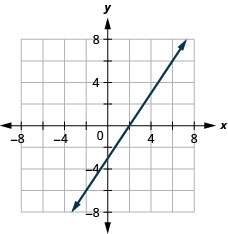
Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line 3 x minus 2 y equals 6 is plotted as an arrow extending from the bottom left toward the top right.$

Graph Vertical and Horizontal lines

In the following exercises, graph each equation.

Exercise $\PageIndex{25}$

$y=-2$

Exercise $\PageIndex{26}$

$x=3$

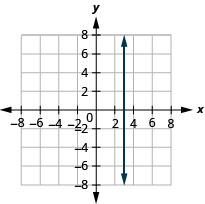
Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line x equals 3 is plotted as a vertical line.$

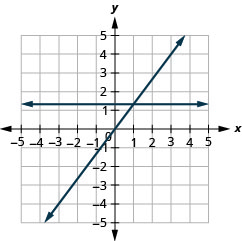
In the following exercises, graph each pair of equations in the same rectangular coordinate system.

Exercise $\PageIndex{27}$

$y=-2 x$ and $y=-2$

Exercise $\PageIndex{28}$

$y=\frac{4}{3} x$ and $y=\frac{4}{3}$

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals four-thirds x is plotted as an arrow extending from the bottom left toward the top right. The line y equals four-thirds is plotted as a horizontal line.$

Graphing with Intercepts

Identify the $x$- and $y$-Intercepts on a Graph

In the following exercises, find the $x$- and $y$-intercepts.

Exercise $\PageIndex{29}$

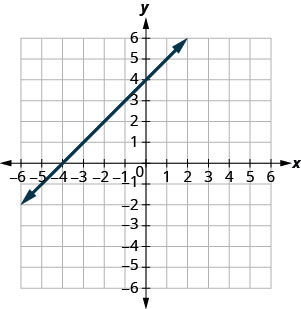
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. A line passing through the points (negative 4, 0) and (0, 4) is plotted.$

Exercise $\PageIndex{30}$

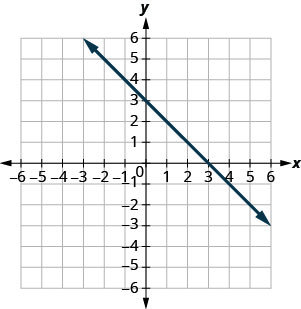
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. A line passing through the points (3, 0) and (0, 3) is plotted.$

Answer: $(3,0)$ and $(0,3)$

Find the$x$- and $y$-Intercepts from an Equation of a Line

In the following exercises, find the intercepts of each equation.

Exercise $\PageIndex{31}$

$x+y=5$

Exercise $\PageIndex{32}$

$x-y=-1$

Answer: $(-1,0),(0,1)$

Exercise $\PageIndex{33}$

$x+2y=6$

Exercise $\PageIndex{34}$

$2x+3y=12$

Answer: $(6,0),(0,4)$

Exercise $\PageIndex{35}$

$y=\frac{3}{4} x-12$

Exercise $\PageIndex{36}$

$y=3x$

Answer: $(0,0)$

Graph a Line Using the Intercepts

In the following exercises, graph using the intercepts.

Exercise $\PageIndex{37}$

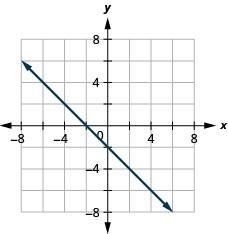
$-x+3y=3$

Exercise $\PageIndex{38}$

$x+y=-2$

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line x plus y equals negative 2 is plotted as an arrow extending from the top left toward the bottom right.$

Exercise $\PageIndex{39}$

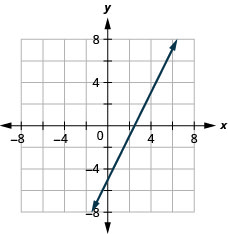
$x-y=4$

Exercise $\PageIndex{40}$

$2x-y=5$

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line 2 x minus y equals 5 is plotted as an arrow extending from the bottom left toward the top right.$

Exercise $\PageIndex{41}$

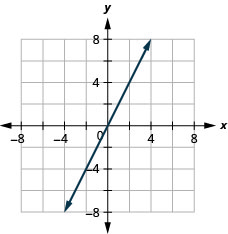
$2x-4y=8$

Exercise $\PageIndex{42}$

$y=2x$

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals 2 x is plotted as an arrow extending from the bottom left toward the top right.$

Slope of a Line

Use Geoboards to Model Slope

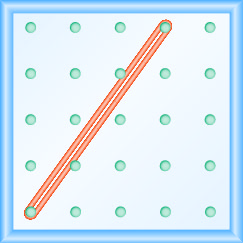
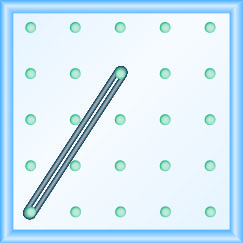
In the following exercises, find the slope modeled on each geoboard.

Exercise $\PageIndex{43}$

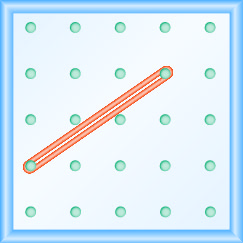
$The figure shows a grid of evenly spaced dots. There are 5 rows and 5 columns. There is a rubber band style loop connecting the point in column 1 row 4 and the point in column 4 row 2.$

Exercise $\PageIndex{44}$

$The figure shows a grid of evenly spaced dots. There are 5 rows and 5 columns. There is a rubber band style loop connecting the point in column 1 row 5 and the point in column 4 row 1.$

Answer: $\frac{4}{3}$

Exercise $\PageIndex{45}$

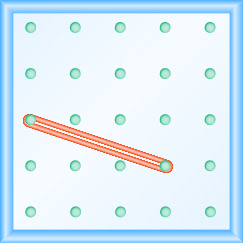
$The figure shows a grid of evenly spaced dots. There are 5 rows and 5 columns. There is a rubber band style loop connecting the point in column 1 row 3 and the point in column 4 row 4.$

Exercise $\PageIndex{46}$

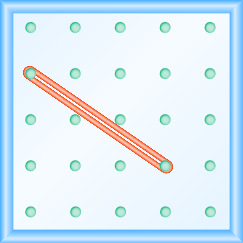
$The figure shows a grid of evenly spaced dots. There are 5 rows and 5 columns. There is a rubber band style loop connecting the point in column 1 row 2 and the point in column 4 row 4.$

Answer: $-\frac{2}{3}$

Exercise $\PageIndex{47}$

$\frac{1}{3}$

Exercise $\PageIndex{48}$

$\frac{3}{2}$

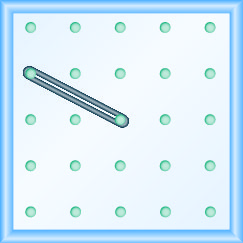
Answer: $The figure shows a grid of evenly spaced dots. There are 5 rows and 5 columns. There is a rubber band style loop connecting the point in column 1 row 5 and the point in column 3 row 2.$

Exercise $\PageIndex{49}$

$-\frac{2}{3}$

Exercise $\PageIndex{50}$

$-\frac{1}{2}$

Answer: $The figure shows a grid of evenly spaced dots. There are 5 rows and 5 columns. There is a rubber band style loop connecting the point in column 2 row 2 and the point in column 3 row 3.$

Use $m=\frac{\text { rise }}{\text { run }}$ to find the Slope of a Line from its Graph

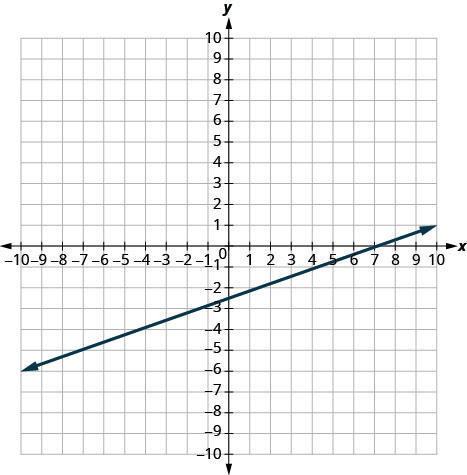
In the following exercises, find the slope of each line shown.

Exercise $\PageIndex{51}$

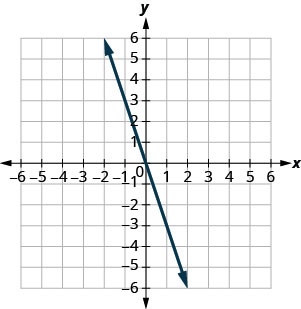
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. A line passing through the points (negative 1, 3), (0, 0), and (1, negative 3) is plotted.$

Exercise $\PageIndex{52}$

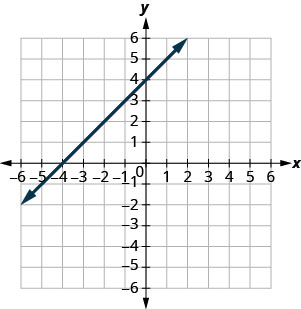
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. A line passing through the points (negative 4, 0) and (0, 4) is plotted.$

Answer: 1

Exercise $\PageIndex{53}$

$alt$

Exercise $\PageIndex{54}$

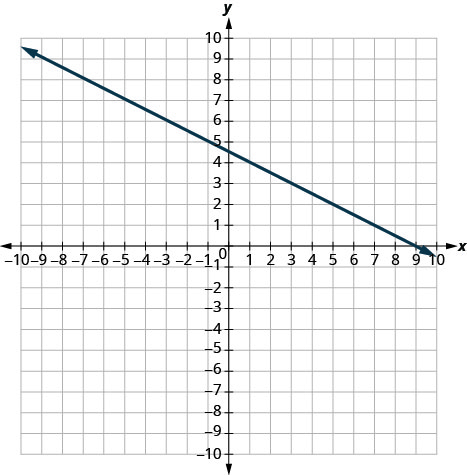
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. A line passing through the points (negative 3, 6) and (5, 2) is plotted.$

Answer: $-\frac{1}{2}$

Find the Slope of Horizontal and Vertical Lines

In the following exercises, find the slope of each line.

Exercise $\PageIndex{55}$

$y=2$

Exercise $\PageIndex{56}$

$x=5$

Answer: undefined

Exercise $\PageIndex{57}$

$x=-3$

Exercise $\PageIndex{58}$

$y=-1$

Answer: 0

Use the Slope Formula to find the Slope of a Line between Two Points

In the following exercises, use the slope formula to find the slope of the line between each pair of points.

Exercise $\PageIndex{59}$

$(-1,-1),(0,5)$

Exercise $\PageIndex{60}$

$(3,5),(4,-1)$

Answer: −6

Exercise $\PageIndex{61}$

$(-5,-2),(3,2)$

Exercise $\PageIndex{62}$

$(2,1),(4,6)$

Answer: $\frac{5}{2}$

Graph a Line Given a Point and the Slope

In the following exercises, graph each line with the given point and slope.

Exercise $\PageIndex{63}$

$(2,-2) ; \quad m=\frac{5}{2}$

Exercise $\PageIndex{64}$

$(-3,4) ; \quad m=-\frac{1}{3}$

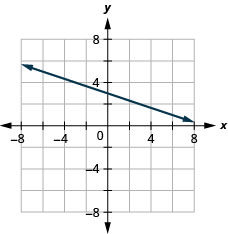
Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. A line passing through the points (negative 3, 4) and (0, 3) is plotted.$

Exercise $\PageIndex{65}$

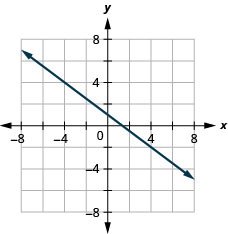
$x$ -intercept $-4 ; \quad m=3$

Exercise $\PageIndex{66}$

$y$ -intercept $1 ; \quad m=-\frac{3}{4}$

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. A line passing through the points (0, 1) and (4, negative 2) is plotted.$

Solve Slope Applications

In the following exercises, solve these slope applications.

Exercise $\PageIndex{67}$

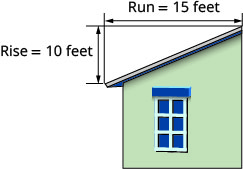
The roof pictured below has a rise of $10$ feet and a run of $15$ feet. What is its slope?

$The figure shows a person on a ladder using a hammer on the roof of a building.$

Exercise $\PageIndex{68}$

A mountain road rises $50$ feet for a $500$-foot run. What is its slope?

Answer: $\frac{1}{10}$

Intercept Form of an Equation of a Line

Recognize the Relation Between the Graph and the Slope–Intercept Form of an Equation of a Line

In the following exercises, use the graph to find the slope and y-intercept of each line. Compare the values to the equation $y=mx+b$.

Exercise $\PageIndex{69}$

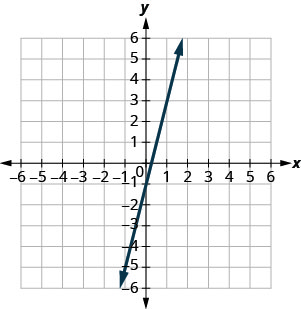
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals 4 x minus 1 is plotted from the lower left to the top right.$

$y=4x−1$

Exercise $\PageIndex{70}$

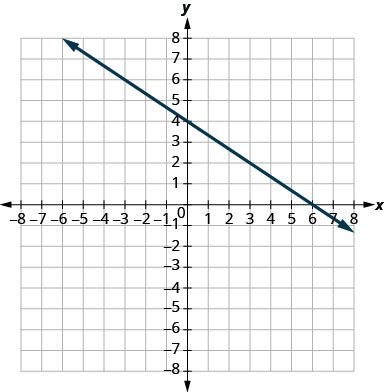
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals two-thirds x plus 4 is plotted from the top left to the bottom right.$

$y=-\frac{2}{3} x+4$

Answer: slope $m=-\frac{2}{3}$ and $y$-intercept $(0,4)$

Identify the Slope and y-Intercept from an Equation of a Line

In the following exercises, identify the slope and $y$-intercept of each line.

Exercise $\PageIndex{71}$

$y=-4 x+9$

Exercise $\PageIndex{72}$

$y=\frac{5}{3} x-6$

Answer: $\frac{5}{3} ;(0,-6)$

Exercise $\PageIndex{73}$

$5x+y=10$

Exercise $\PageIndex{74}$

$4x-5y=8$

Answer: $\frac{4}{5} ;\quad \left(0,-\frac{8}{5}\right)$

Graph a Line Using Its Slope and Intercept

In the following exercises, graph the line of each equation using its slope and $y$-intercept.

Exercise $\PageIndex{75}$

$y=2x+3$

Exercise $\PageIndex{76}$

$y=-x-1$

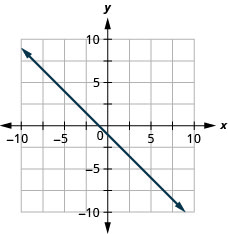
Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals negative x minus 1 is plotted from the top left to the bottom right.$

Exercise $\PageIndex{77}$

$y=-\frac{2}{5} x+3$

Exercise $\PageIndex{78}$

$4x-3y=12$

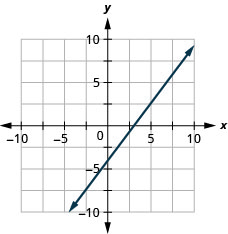
Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line 4 x minus 3 y equals 12 is plotted from the bottom left to the top right.$

In the following exercises, determine the most convenient method to graph each line.

Exercise $\PageIndex{79}$

$x=5$

Exercise $\PageIndex{80}$

$y=-3$

Answer: horizontal line

Exercise $\PageIndex{81}$

$2x+y=5$

Exercise $\PageIndex{82}$

$x-y=2$

Answer: intercepts

Exercise $\PageIndex{83}$

$y=x+2$

Exercise $\PageIndex{84}$

$y=\frac{3}{4} x-1$

Answer: plotting points

Graph and Interpret Applications of Slope–Intercept

Exercise $\PageIndex{85}$

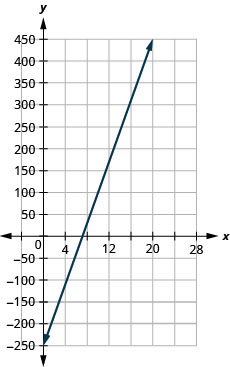
Katherine is a private chef. The equation $C=6.5m+42$ models the relation between her weekly cost, $C$, in dollars and the number of meals, $m$, that she serves.

Find Katherine’s cost for a week when she serves no meals.
Find the cost for a week when she serves $14$ meals.
Interpret the slope and $C$-intercept of the equation.
Graph the equation.

Exercise $\PageIndex{86}$

Marjorie teaches piano. The equation $P=35h−250$ models the relation between her weekly profit, $P$, in dollars and the number of student lessons, $s$, that she teaches.

Find Marjorie’s profit for a week when she teaches no student lessons.
Find the profit for a week when she teaches $20$ student lessons.
Interpret the slope and $P$-intercept of the equation.
Graph the equation.

Answer

$−$250$
$$450$
The slope, $35$, means that Marjorie’s weekly profit, $P$, increases by $$35$ for each additional student lesson she teaches. The $P$-intercept means that when the number of lessons is $0$, Marjorie loses $$250$.

$The graph shows the x y-coordinate plane where h is plotted along the x-axis and P is potted along the y-axis. The x-axis runs from 0 to 24. The y-axis runs from negative 300 to 500. The line P equals 35 h minus 250 is plotted from the bottom left to the top right.$

Use Slopes to Identify Parallel Lines

In the following exercises, use slopes and $y$-intercepts to determine if the lines are parallel.

Exercise $\PageIndex{87}$

$4x-3y=-1 ; \quad y=\frac{4}{3} x-3$

Exercise $\PageIndex{88}$

$2 x-y=8 ; \quad x-2 y=4$

Answer: not parallel

Use Slopes to Identify Perpendicular Lines

In the following exercises, use slopes and y-intercepts to determine if the lines are perpendicular.

Exercise $\PageIndex{89}$

$y=5x-1 ; \quad 10x+2y=0$

Exercise $\PageIndex{90}$

$3x-2y=5 ; \quad 2x+3y=6$

Answer: perpendicular

Find the Equation of a Line

Find an Equation of the Line Given the Slope and y-Intercept

In the following exercises, find the equation of a line with given slope and $y$-intercept. Write the equation in slope–intercept form.

Exercise $\PageIndex{91}$

slope $\frac{1}{3}$ and $y$-intercept $(0,-6)$

Exercise $\PageIndex{92}$

slope $-5$ and $y$-intercept $(0,-3)$

Answer: $y=-5x-3$

Exercise $\PageIndex{93}$

slope $0$ and $y$-intercept $(0,4)$

Exercise $\PageIndex{94}$

slope $-2$ and $y$-intercept $(0,0)$

Answer: $y=-2x$

In the following exercises, find the equation of the line shown in each graph. Write the equation in slope–intercept form.

Exercise $\PageIndex{95}$

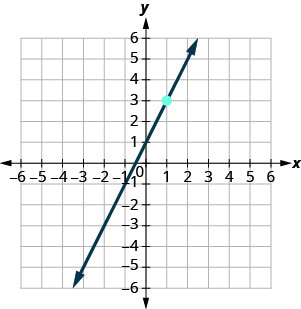
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals 2 x plus 1 is plotted from the bottom left to the top right.$

Exercise $\PageIndex{96}$

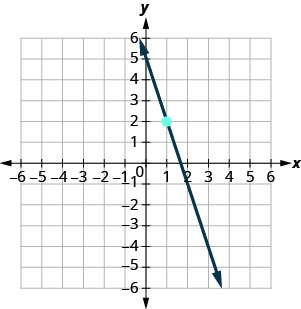
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals negative 3 x plus 5 is plotted from the top left to the bottom right.$

Answer: $y=-3x+5$

Exercise $\PageIndex{97}$

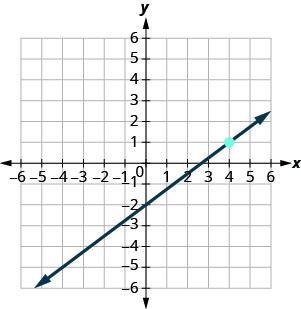
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals three-fourths x minus 2 is plotted from the bottom left to the top right.$

Exercise $\PageIndex{98}$

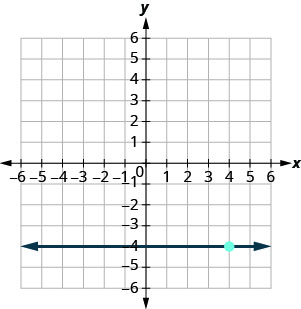
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals negative 4 is plotted as a horizontal line.$

Answer: $y=-4$

Find an Equation of the Line Given the Slope and a Point

In the following exercises, find the equation of a line with given slope and containing the given point. Write the equation in slope–intercept form.

Exercise $\PageIndex{99}$

$m=-\frac{1}{4},$ point $(-8,3)$

Exercise $\PageIndex{100}$

$m=\frac{3}{5},$ point $(10,6)$

Answer: $y=\frac{3}{5} x$

Exercise $\PageIndex{101}$

Horizontal line containing $(-2,7)$

Exercise $\PageIndex{102}$

$m=-2,$ point $(-1,-3)$

Answer: $y=-2x-5$

Find an Equation of the Line Given Two Points

In the following exercises, find the equation of a line containing the given points. Write the equation in slope–intercept form.

Exercise $\PageIndex{103}$

$(2,10)$ and $(-2,-2)$

Exercise $\PageIndex{104}$

$(7,1)$ and $(5,0)$

Answer: $y=\frac{1}{2} x-\frac{5}{2}$

Exercise $\PageIndex{105}$

$(3,8)$ and $(3,-4)$

Exercise $\PageIndex{106}$

$(5,2)$ and $(-1,2)$

Answer: $y=2$

Find an Equation of a Line Parallel to a Given Line

In the following exercises, find an equation of a line parallel to the given line and contains the given point. Write the equation in slope–intercept form.

Exercise $\PageIndex{107}$

line $y=-3x+6,$ point $(1,-5)$

Exercise $\PageIndex{108}$

line $2x+5y=-10,$ point $(10,4)$

Answer: $y=-\frac{2}{5} x+8$

Exercise $\PageIndex{109}$

line $x=4,$ point $(-2,-1)$

Exercise $\PageIndex{110}$

line $y=-5,$ point $(-4,3)$

Answer: $y=3$

Find an Equation of a Line Perpendicular to a Given Line

In the following exercises, find an equation of a line perpendicular to the given line and contains the given point. Write the equation in slope–intercept form.

Exercise $\PageIndex{111}$

line $y=-\frac{4}{5} x+2,$ point $(8,9)$

Exercise $\PageIndex{112}$

line $2x-3y=9,$ point $(-4,0)$

Answer: $y=-\frac{3}{2} x-6$

Exercise $\PageIndex{113}$

line $y=3,$ point $(-1,-3)$

Exercise $\PageIndex{114}$

line $x=-5$ point $(2,1)$

Answer: $y=1$

Graph Linear Inequalities

Verify Solutions to an Inequality in Two Variables

In the following exercises, determine whether each ordered pair is a solution to the given inequality.

Exercise $\PageIndex{115}$

Determine whether each ordered pair is a solution to the inequality $y<x−3$:

$(0,1)$
$(−2,−4)$
$(5,2)$
$(3,−1)$
$(−1,−5)$

Exercise $\PageIndex{116}$

Determine whether each ordered pair is a solution to the inequality $x+y>4$:

$(6,1)$
$(−3,6)$
$(3,2)$
$(−5,10)$
$(0,0)$

Answer

Recognize the Relation Between the Solutions of an Inequality and its Graph

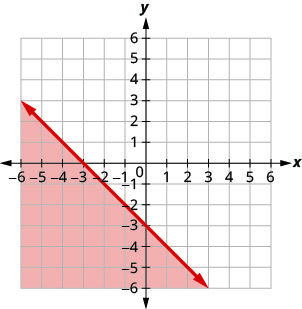
In the following exercises, write the inequality shown by the shaded region.

Exercise $\PageIndex{117}$

Write the inequality shown by the graph with the boundary line $y=−x+2$.

$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals negative x plus 2 is plotted as a solid line extending from the top left toward the bottom right. The region below the line is shaded.$

Exercise $\PageIndex{118}$

Write the inequality shown by the graph with the boundary line $y=\frac{2}{3} x-3$

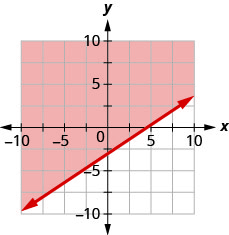
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals two-thirds x minus 3 is plotted as a dashed line extending from the bottom left toward the top right. The region above the line is shaded.$

Answer: $y>\frac{2}{3} x-3$

Exercise $\PageIndex{119}$

Write the inequality shown by the shaded region in the graph with the boundary line $x+y=−4$.

$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line x plus y equals negative 4 is plotted as a dashed line extending from the top left toward the bottom right. The region above the line is shaded.$

Exercise $\PageIndex{120}$

Write the inequality shown by the shaded region in the graph with the boundary line $x−2y=6$.

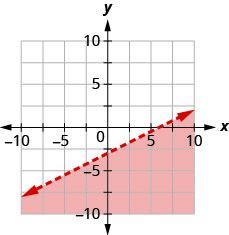
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line x minus 2 y equals 6 is plotted as a solid line extending from the bottom left toward the top right. The region below the line is shaded.$

Answer: $x-2 y \geq 6$

Graph Linear Inequalities

In the following exercises, graph each linear inequality.

Exercise $\PageIndex{121}$

Graph the linear inequality $y>\frac{2}{5} x-4$

Exercise $\PageIndex{122}$

Graph the linear inequality $y \leq-\frac{1}{4} x+3$

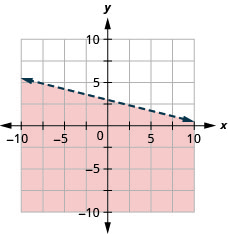
Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals negative one-fourth x plus 3 is plotted as a solid line extending from the top left toward the bottom right. The region below the line is shaded.$

Exercise $\PageIndex{123}$

Graph the linear inequality $x-y \leq 5$

Exercise $\PageIndex{124}$

Graph the linear inequality $3 x+2 y>10$

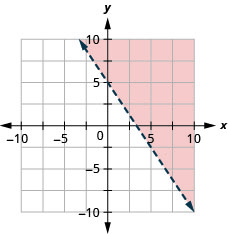
Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line 3 x plus 2 y equals 10 is plotted as a dashed line extending from the top left toward the bottom right. The region above the line is shaded.$

Exercise $\PageIndex{125}$

Graph the linear inequality $y \leq-3 x$

Exercise $\PageIndex{126}$

Graph the linear inequality $y<6$

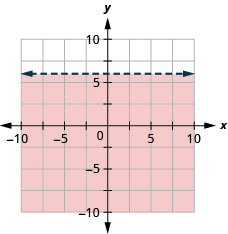
Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals 6 is plotted as a dashed, horizontal line. The region below the line is shaded.$

Practice Test

Exercise $\PageIndex{1}$

Plot each point in a rectangular coordinate system.

$(2,5)$
$(−1,−3)$
$(0,2)$
$\left(-4, \frac{3}{2}\right)$
$(5,0)$

Exercise $\PageIndex{2}$

Which of the given ordered pairs are solutions to the equation $3x−y=6$?

$(3,3)$
$(2,0)$
$(4,−6)$

Answer

Exercise $\PageIndex{3}$

Find three solutions to the linear equation $y=-2x-4$

Exercise $\PageIndex{4}$

Find the $x$- and $y$-intercepts of the equation $4x-3y=12$

Answer: $(3,0),(0,-4)$

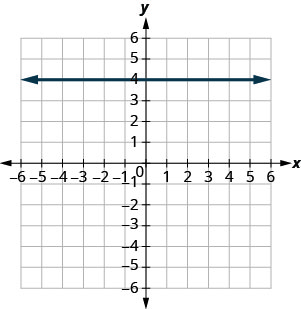
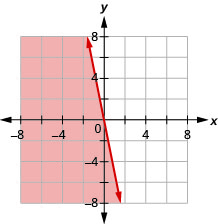
Find the slope of each line shown.

Exercise $\PageIndex{5}$

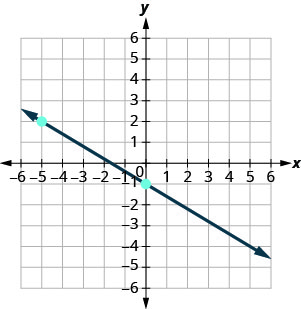
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. A line passing through the points (negative 5, 2) and (0, negative 1) is plotted from the top left toward the bottom right.$

Exercise $\PageIndex{6}$

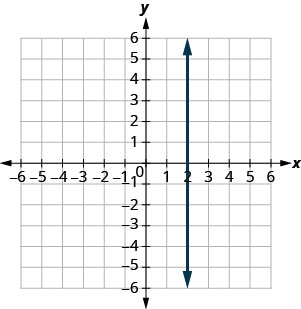
$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. A vertical line passing through the point (2, 0) is plotted.$

Answer: undefined

Exercise $\PageIndex{7}$

$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. A horizontal line passing through the point (0, 5) is plotted.$

Exercise $\PageIndex{8}$

Find the slope of the line between the points $(5,2)$ and $(-1,-4)$

Answer: 1

Exercise $\PageIndex{9}$

Graph the line with slope $\frac{1}{2}$ containing the point $(-3,-4)$

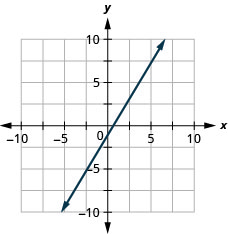
Graph the line for each of the following equations.

Exercise $\PageIndex{10}$

$y=\frac{5}{3} x-1$

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals five-thirds x minus 1 is plotted. The line passes through the points (0, negative 1) and (three-fifths, 0).$

Exercise $\PageIndex{11}$

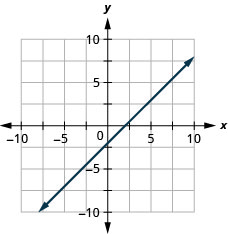
$y=-x$

Exercise $\PageIndex{12}$

$x-y=2$

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line x minus y equals 2 is plotted. The line passes through the points (0, negative 2) and (2, 0).$

Exercise $\PageIndex{13}$

$4x+2y=-8$

Exercise $\PageIndex{14}$

$y=2$

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals 2 is plotted as a horizontal line passing through the point (0, 2).$

Exercise $\PageIndex{15}$

$x=-3$

Find the equation of each line. Write the equation in slope–intercept form.

Exercise $\PageIndex{16}$

slope $-\frac{3}{4}$ and $y$-intercept $(0,-2)$

Answer: $y=-\frac{3}{4} x-2$

Exercise $\PageIndex{17}$

$m=2,$ point $(-3,-1)$

Exercise $\PageIndex{18}$

containing $(10,1)$ and $(6,-1)$

Answer: $y=\frac{1}{2} x-4$

Exercise $\PageIndex{19}$

parallel to the line $y=-\frac{2}{3} x-1,$ containing the point $(-3,8)$

Exercise $\PageIndex{20}$

perpendicular to the line $y=\frac{5}{4} x+2,$ containing the point $(-10,3)$

Answer: $y=-\frac{4}{5} x-5$

Exercise $\PageIndex{21}$

Write the inequality shown by the graph with the boundary line $y=−x−3$.

$The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals negative x minus 3 is plotted. The solid line passes through the points (negative 3, 0) and (0, negative 3).$

Graph each linear inequality.

Exercise $\PageIndex{22}$

$y>\frac{3}{2} x+5$

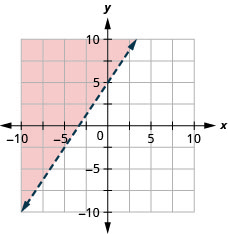
Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals three-halves x plus 5 is plotted. The dashed line passes through the points (0, 5) and (2, 8).$

Exercise $\PageIndex{23}$

$x-y \geq-4$

Exercise $\PageIndex{24}$

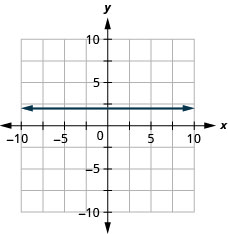
$y \leq-5 x$

Answer: $The graph shows the x y-coordinate plane. The x- and y-axes each run from negative 7 to 7. The line y equals negative 5 x is plotted. The solid line passes through the points (0, 0) and (1, negative 5).$

Exercise $\PageIndex{1}$

$y<3$

Chapter 4 Review Exercises

Rectangular Coordinate System

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Exercise \(\PageIndex{13}\)

Exercise \(\PageIndex{14}\)

Exercise \(\PageIndex{15}\)

Exercise \(\PageIndex{16}\)

Graphing Linear Equations

Exercise \(\PageIndex{17}\)

Exercise \(\PageIndex{18}\)

Exercise \(\PageIndex{19}\)

Exercise \(\PageIndex{20}\)

Exercise \(\PageIndex{21}\)

Exercise \(\PageIndex{22}\)

Exercise \(\PageIndex{23}\)

Exercise \(\PageIndex{24}\)

Exercise \(\PageIndex{25}\)

Exercise \(\PageIndex{26}\)

Exercise \(\PageIndex{27}\)

Exercise \(\PageIndex{28}\)

Graphing with Intercepts

Exercise \(\PageIndex{29}\)

Exercise \(\PageIndex{30}\)

Exercise \(\PageIndex{31}\)

Exercise \(\PageIndex{32}\)

Exercise \(\PageIndex{33}\)

Exercise \(\PageIndex{34}\)

Exercise \(\PageIndex{35}\)

Exercise \(\PageIndex{36}\)

Exercise \(\PageIndex{37}\)

Exercise \(\PageIndex{38}\)

Exercise \(\PageIndex{39}\)

Exercise \(\PageIndex{40}\)

Exercise \(\PageIndex{41}\)

Exercise \(\PageIndex{42}\)

Slope of a Line

Exercise \(\PageIndex{43}\)

Exercise \(\PageIndex{44}\)

Exercise \(\PageIndex{45}\)

Exercise \(\PageIndex{46}\)

Exercise \(\PageIndex{47}\)

Exercise \(\PageIndex{48}\)

Exercise \(\PageIndex{49}\)

Exercise \(\PageIndex{50}\)

Exercise \(\PageIndex{51}\)

Exercise \(\PageIndex{52}\)

Exercise \(\PageIndex{53}\)

Exercise \(\PageIndex{54}\)

Exercise \(\PageIndex{55}\)

Exercise \(\PageIndex{56}\)

Exercise \(\PageIndex{57}\)

Exercise \(\PageIndex{58}\)

Exercise \(\PageIndex{59}\)

Exercise \(\PageIndex{60}\)

Exercise \(\PageIndex{61}\)

Exercise \(\PageIndex{62}\)

Exercise \(\PageIndex{63}\)

Exercise \(\PageIndex{64}\)

Exercise \(\PageIndex{65}\)

Exercise \(\PageIndex{66}\)

Exercise \(\PageIndex{67}\)

Exercise \(\PageIndex{68}\)

Intercept Form of an Equation of a Line

Exercise \(\PageIndex{69}\)

Exercise \(\PageIndex{70}\)

Exercise \(\PageIndex{71}\)

Exercise \(\PageIndex{72}\)

Exercise \(\PageIndex{73}\)

Exercise \(\PageIndex{74}\)