7.2: Reducing Rational Functions
- Page ID
- 19721
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The goal of this section is to learn how to reduce a rational expression to “lowest terms.” Of course, that means that we will have to understand what is meant by the phrase “lowest terms.” With that thought in mind, we begin with a discussion of the greatest common divisor of a pair of integers.
First, we define what we mean by “divisibility.”
Suppose that we have a pair of integers a and b. We say that “a is a divisor of b,” or “a divides b” if and only if there is another integer k so that b = ak. Another way of saying the same thing is to say that a divides b if, upon dividing b by a, the remainder is zero.
Let’s look at an example.
What are the divisors of 12?
Solution
Because \(12=1 \times 12\), both 1 and 12 are divisors of 12. Because \(12=2 \times 6\), both 2 and 6 are divisors of 12. Finally, because \(12=3 \times 4\), both 3 and 4 are divisors of 12. If we list them in ascending order, the divisors of 12 are \[1,2,3,4,6, \text { and } 12 \nonumber \]
Let’s look at another example.
What are the divisors of 18?
Solution
Because \(18=1 \times 18\), both 1 and 18 are divisors of 18. Similarly, \(18=2 \times 9\) and \(18=3 \times 6\), so in ascending order, the divisors of 18 are
\[1,2,3,6,9, \text { and } 18 \nonumber \]
The greatest common divisor of two or more integers is the largest divisor the integers share in common. An example should make this clear.
What is the greatest common divisor of 12 and 18?
Solution
In Example 2 and Example 3, we saw the following.
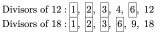
We’ve framed the divisors that 12 and 18 have in common. They are 1, 2, 3, and 6. The “greatest” of these “common” divisors is 6. Hence, we say that “the greatest common divisor of 12 and 18 is 6.”
The greatest common divisor of two integers a and b is the largest divisor they have in common. We will use the notation \[GCD(a, b) \nonumber \] to represent the greatest common divisor of a and b.
Thus, as we saw in Example 4, GCD(12, 18) = 6.
When the greatest common divisor of a pair of integers is one, we give that pair a special name.
Let a and b be integers. If the greatest common divisor of a and b is one, that is, if GCD(a, b) = 1, then we say that a and b are relatively prime.
For example:
- 9 and 12 are not relatively prime because GCD(9, 12) = 3.
- 10 and 15 are not relatively prime because GCD(10, 15) = 5.
- 8 and 21 are relatively prime because GCD(8, 21) = 1.
We can now define what is meant when we say that a rational number is reduced to lowest terms.
A rational number in the form p/q, where p and q are integers, is said to be reduced to lowest terms if and only if GCD(p, q) = 1. That is, p/q is reduced to lowest terms if the greatest common divisor of both numerator and denominator is 1.
As we saw in Example \(\PageIndex{3}\), the greatest common divisor of 12 and 18 is 6. Therefore, the fraction 12/18 is not reduced to lowest terms. However, we can reduce 12/18 to lowest terms by dividing both numerator and denominator by their greatest common divisor. That is,
\[\frac{12}{18}=\frac{12 \div 6}{18 \div 6}=\frac{2}{3} \nonumber \]
Note that GCD(2, 3) = 1, so 2/3 is reduced to lowest terms.
When it is difficult to ascertain the greatest common divisor, we’ll find it more efficient to proceed as follows:
• Prime factor both numerator and denominator.
• Cancel common factors.
Thus, to reduce 12/18 to lowest terms, first express both numerator and denominator as a product of prime numbers, then cancel common primes.
\[\frac{12}{18}=\frac{2 \cdot 2 \cdot 3}{2 \cdot 3 \cdot 3}=\frac{\not{2} \cdot 2 \cdot \not{3}}{\not{2} \cdot 3 \cdot \not{3}}=\frac{2}{3} \nonumber \]
When you cancel a 2, you’re actually dividing both numerator and denominator by 2. When you cancel a 3, you’re actually dividing both numerator and denominator by 3. Note that doing both (dividing by 2 and then dividing by 3) is equivalent to dividing both numerator and denominator by 6.
We will favor this latter technique, precisely because it is identical to the technique we will use to reduce rational functions to lowest terms. However, this “cancellation” technique has some pitfalls, so let’s take a moment to discuss some common cancellation mistakes.
Cancellation
You can spark some pretty heated debate amongst mathematics educators by innocently mentioning the word “cancellation.” There seem to be two diametrically opposed camps, those who don’t mind when their students use the technique of cancellation, and on the other side, those that refuse to even use the term “cancellation” in their classes.
Both sides of the argument have merit. As we showed in equation (8), we can reduce 12/18 quite efficiently by simply canceling common factors. On the other hand, instructors from the second camp prefer to use the phrase “factor out a 1” instead of the phrase “cancel,” encouraging their students to reduce 12/18 as follows.
\[\frac{12}{18}=\frac{2 \cdot 2 \cdot 3}{2 \cdot 3 \cdot 3}=\frac{2}{3} \cdot \color{blue}{\frac{2 \cdot 3}{2 \cdot 3}}=\frac{2}{3} \cdot 1=\frac{2}{3} \nonumber \]
This is a perfectly valid technique and one that, quite honestly, avoids the quicksand of “cancellation mistakes.” Instructors who grow weary of watching their students “cancel” when they shouldn’t are quite likely to promote this latter technique.
However, if we can help our students avoid “cancellation mistakes,” we prefer to allow our students to cancel common factors (as we did in equation (8)) when reducing fractions such as 12/18 to lowest terms. So, with these thoughts in mind, let’s discuss some of the most common cancellation mistakes.
Let’s begin with a most important piece of advice.
You may only cancel factors, not addends. To avoid cancellation mistakes, factor completely before you begin to cancel.
Many of the ensuing calculations are incorrect. They are examples of common mistakes that are made when performing cancellation. Make sure that you read carefully and avoid just “scanning” these calculations.
As a first example, consider the rational expression
\[\frac{2+6}{2} \nonumber \]
which clearly equals 8/2, or 4. However, if you cancel in this situation, as in
\[\frac{2+6}{2}=\frac{\not{2}+6}{\not{2}} \nonumber \]
you certainly do not get the same result. So, what happened?
Note that in the numerator of equation (10), the 2 and the 6 are separated by a plus sign. Thus, they are not factors; they are addends! You are not allowed to cancel addends, only factors.
Suppose, for comparison, that the rational expression had been
\[\frac{2 \cdot 6}{2} \nonumber \]
which clearly equals 12/2, or 6. In this case, the 2 and the 6 in the numerator are separated by a multiplication symbol, so they are factors and cancellation is allowed, as in
\[\frac{2 \cdot 6}{2}=\frac{\not{2} \cdot 6}{\not{2}}=6 \nonumber \]
Now, before you dismiss these examples as trivial, consider the following examples which are identical in structure. First, consider
\[\frac{x+(x+2)}{x}=\frac{\not{x}+(x+2)}{\not{x}}=x+2 \nonumber \]
This cancellation is identical to that performed in equation (10) and is not allowed. In the numerator, note that x and (x+2) are separated by an addition symbol, so they are addends. You are not allowed to cancel addends!
Conversely, consider the following example.
\[\frac{x(x+2)}{x}=\frac{\not{x}(x+2)}{\not{x}}=x+2 \nonumber \]
In the numerator of this example, x and (x+2) are separated by implied multiplication. Hence, they are factors and cancellation is permissible.
Look again at equation (10), where the correct answer should have been 8/2, or 4. We mistakenly found the answer to be 6, because we cancelled addends. A workaround would be to first factor the numerator of equation (10), then cancel, as follows.
\[\frac{2+6}{2}=\frac{2(1+3)}{2}=\frac{\not{2}(1+3)}{\not{2}}=1+3=4 \nonumber \]
Note that we cancelled factors in this approach, which is permissible, and got the correct answer 4.
We are finished discussing common cancellation mistakes and you may not continue reading with confidence that all mathematics is correctly presented.
Reducing Rational Expressions in x
Now that we’ve discussed some fundamental ideas and techniques, let’s apply what we’ve learned to rational expressions that are functions of an independent variable (usually x). Let’s start with a simple example.
Reduce the rational expression \[\frac{2 x-6}{x^{2}-7 x+12} \nonumber \] to lowest terms. For what values of x is your result valid?
Solution
In the numerator, factor out a 2, as in 2x − 6 = 2(x − 3).
The denominator is a quadratic trinomial with ac = (1)(12) = 12. The integer pair −3 and −4 has product 12 and sum −7, so the denominator factors as shown.
\[\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(x-3)}{(x-3)(x-4)} \nonumber \]
Now that both numerator and denominator are factored, we can cancel common factors.
\[\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(x-3)}{(x-3)(x-4)}=\frac{2}{x-4} \nonumber \]
Thus, we have shown that \[\frac{2 x-6}{x^{2}-7 x+12}=\frac{2}{x-4} \nonumber \]
In equation (15), we are stating that the expression on the left (the original expression) is identical to the expression on the right for all values of x.
Actually, there are two notable exceptions, the first of which is x = 3. If we substitute x = 3 into the left-hand side of equation (15), we get
\[\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(3)-6}{(3)^{2}-7(3)+12}=\frac{0}{0} \nonumber \]
We cannot divide by zero, so the left-hand side of equation (15) is undefined if x = 3. Therefore, the result in equation (15) is not valid if x = 3.
Similarly, if we insert x = 4 in the left-hand side of equation (15),
\[\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(4)-6}{(4)^{2}-7(4)+12}=\frac{2}{0} \nonumber \]
Again, division by zero is undefined. The left-hand side of equation (15) is undefined if x = 4, so the result in equation (15) is not valid if x = 4. Note that the right-hand side of equation (15) is also undefined at x = 4.
However, the algebraic work we did above guarantees that the left-hand side of equation (15) will be identical to the right-hand side of equation (15) for all other values of x. For example, if we substitute x = 5 into the left-hand side of equation (15),
\[\frac{2 x-6}{x^{2}-7 x+12}=\frac{2(5)-6}{(5)^{2}-7(5)+12}=\frac{4}{2}=2 \nonumber \]
On the other hand, if we substitute x = 5 into the right-hand side of equation (15),
\[\frac{2}{x-4}=\frac{2}{5-4}=2 \nonumber \]
Hence, both sides of equation (15) are identical when x = 5. In a similar manner, we could check the validity of the identity in equation (15) for all other values of x
You can use the graphing calculator to verify the identity in equation (15). Load the left- and right-hand sides of equation (15) in Y= menu, as shown in Figure \(\PageIndex{1}\)(a). Press 2nd TBLSET and adjust settings as shown in Figure \(\PageIndex{1}\)(b). Be sure that you highlight AUTO for both independent and dependent variables and press ENTER on each to make the selection permanent. In Figure \(\PageIndex{1}\)(b), note that we’ve set TblStart = 0 and ∆Tbl = 1. Press 2nd TABLE to produce the tabular results shown in Figure \(\PageIndex{1}\)(c).
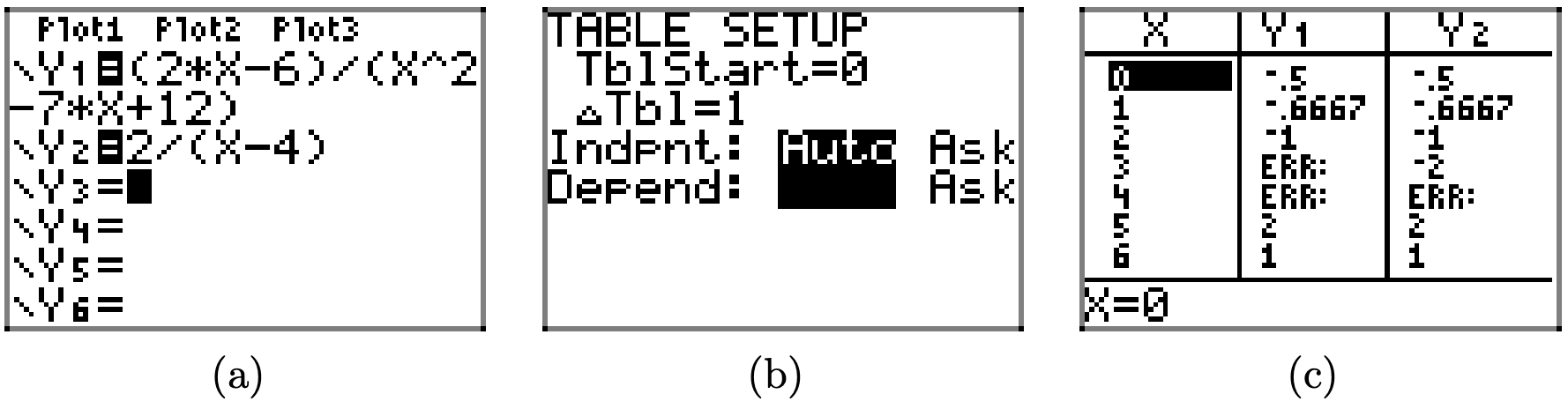
Remember that we placed the left- and right-hand sides of equation (15) in Y1 and Y2, respectively.
- In the tabular results of Figure \(\PageIndex{1}\)(c), note the ERR (error) message in Y1 when x = 3 and x = 4. This agrees with our findings above, where the left-hand side of equation (15) was undefined because of the presence of zero in the denominator when x = 3 or x = 4.
- In the tabular results of Figure \(\PageIndex{1}\)(c), note that the value of Y1 and Y2 agree for all other values of x.
We are led to the following key result.
In general, when you reduce a rational expression to lowest terms, the expression obtained should be identical to the original expression for all values of the variables in each expression, save those values of the variables that make any denominator equal to zero. This applies to the denominator in the original expression, all intermediate expressions in your work, and the final result. We will refer to any values of the variable that make any denominator equal to zero as restrictions.
Let’s look at another example.
Reduce the expression \[\frac{2 x^{2}+5 x-12}{4 x^{3}+16 x^{2}-9 x-36} \nonumber \] to lowest terms. State all restrictions.
Solution
The numerator is a quadratic trinomial with ac = (2)(−12) = −24. The integer pair −3 and 8 have product −24 and sum 5. Break the middle term of the polynomial in the numerator into a sum using this integer pair, then factor by grouping.
\[\begin{aligned} 2 x^{2}+5 x-12 &=2 x^{2}-3 x+8 x-12 \\ &=x(2 x-3)+4(2 x-3) \\ &=(x+4)(2 x-3) \end{aligned} \nonumber \]
Factor the denominator by grouping.
\[\begin{aligned} 4 x^{3}+16 x^{2}-9 x-36 &=4 x^{2}(x+4)-9(x+4) \\ &=\left(4 x^{2}-9\right)(x+4) \\ &=(2 x+3)(2 x-3)(x+4) \end{aligned} \nonumber \]
Note how the difference of two squares pattern was used to factor \(4x^2 − 9 = (2x + 3)(2x − 3)\) in the last step.
Now that we’ve factored both numerator and denominator, we cancel common factors.
\[\begin{aligned} \frac{2 x^{2}+5 x-12}{4 x^{3}+16 x^{2}-9 x-36} &=\frac{(x+4)(2 x-3)}{(2 x+3)(2 x-3)(x+4)} \\ &=\frac{(x+4)(2 x-3)}{(2 x+3)(2 x-3)(x+4)} \\ &=\frac{1}{2 x+3} \end{aligned} \nonumber \]
We must now determine the restrictions. This means that we must find those values of x that make any denominator equal to zero.
- In the body of our work, we have the denominator (2x + 3)(2x − 3)(x + 4). If we set this equal to zero, the zero product property implies that \[2 x+3=0 \quad \text { or } \quad 2 x-3=0 \quad \text { or } \quad x+4=0 \nonumber \]
Each of these linear factors can be solved independently \[x=-3 / 2 \quad \text { or } \quad x=3 / 2 \quad \text { or } \quad x=-4 \nonumber \]
Each of these x-values is a restriction.
- In the final rational expression, the denominator is 2x + 3. This expression equals zero when x = −3/2 and provides no new restrictions.
- Because the denominator of the original expression, namely \(4 x^{3}+16 x^{2}-9 x-36\), is identical to its factored form in the body our work, this denominator will produce no new restrictions.
Thus, for all values of x \[\frac{2 x^{2}+5 x-12}{4 x^{3}+16 x^{2}-9 x-36}=\frac{1}{2 x+3} \nonumber \]
provided \(x \neq −3/2, 3/2, or −4\). These are the restrictions. The two expressions are identical for all other values of x.
Finally, let’s check this result with our graphing calculator. Load each side of equation (18) into the Y= menu, as shown in Figure \(\PageIndex{2}\)(a). We know that we have a restriction at x = −3/2, so let’s set TblStart = −2 and \(\Delta \mathrm{Tbl}=0.5\), as shown in Figure \(\PageIndex{2}\)(b). Be sure that you have AUTO set for both independent and dependent variables. Push the TABLE button to produce the tabular display shown in Figure \(\PageIndex{2}\)(c).

Remember that we placed the left- and right-hand sides of equation (18) in Y1 and Y2, respectively.
- In Figure \(\PageIndex{2}\)(c), note that the expressions Y1 and Y2 agree at all values of x except x = −1.5. This is the restriction −3/2 we found above.
- Use the down arrow key to scroll down in the table shown in Figure \(\PageIndex{2}\)(c) to produce the tabular view shown in Figure \(\PageIndex{2}\)(d). Note that Y1 and Y2 agree for all values of x except x = 1.5. This is the restriction 3/2 we found above.
- We leave it to our readers to uncover the restriction at x = −4 by using the uparrow to scroll up in the table until you reach an x-value of −4. You should uncover another ERR (error) message at this x-value because it is a restriction. You get the ERR message due to the fact that the denominator of the left-hand side of equation (18) is zero at x = −4.
Sign Changes
It is not uncommon that you will have to manipulate the signs in a fraction in order to obtain common factors that can be then cancelled. Consider, for example, the rational expression
\[\frac{3-x}{x-3} \nonumber \]
One possible approach is to factor −1 out of the numerator to obtain
\[\frac{3-x}{x-3}=\frac{-(x-3)}{x-3} \nonumber \]
You can now cancel common factors.
\[\frac{3-x}{x-3}=\frac{-(x-3)}{x-3}=\frac{-(x-3)}{x-3}=-1 \nonumber \]
This result is valid for all values of x, provided \(x \neq 3\).
Let’s look at another example.
Reduce the rational expression \[\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4} \nonumber \] to lowest terms. State all restrictions.
Solution
In the numerator, factor out 2x, then complete the factorization using the difference of two squares pattern.
\[2 x-2 x^{3}=2 x\left(1-x^{2}\right)=2 x(1+x)(1-x) \nonumber \]
The denominator can be factored by grouping.
\[\begin{aligned} 3 x^{3}+4 x^{2}-3 x-4 &=x^{2}(3 x+4)-1(3 x+4) \\ &=\left(x^{2}-1\right)(3 x+4) \\ &=(x+1)(x-1)(3 x+4) \end{aligned} \nonumber \]
Note how the difference of two squares pattern was applied in the last step.
At this point, \[\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}=\frac{2 x(1+x)(1-x)}{(x+1)(x-1)(3 x+4)} \nonumber \]
Because we have 1 − x in the numerator and x − 1 in the denominator, we will factor out a −1 from 1 − x, and because the order of factors does not affect their product, we will move the −1 out to the front of the numerator.
\[\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}=\frac{2 x(1+x)(-1)(x-1)}{(x+1)(x-1)(3 x+4)}=\frac{-2 x(1+x)(x-1)}{(x+1)(x-1)(3 x+4)} \nonumber \]
We can now cancel common factors.
\[\begin{aligned} \frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4} &=\frac{-2 x(1+x)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=\frac{-2 x(1+x)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=\frac{-2 x}{3 x+4} \end{aligned} \nonumber \]
Note that x + 1 is identical to 1 + x and cancels. Thus,
\[\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}=\frac{-2 x}{3 x+4} \nonumber \]
for all values of x, provided \(x \neq-1,1,\) or \(-4 / 3\). These are the restrictions, values of x that make denominators equal to zero.
The Sign Change Rule for Fractions
Let’s look at an alternative approach to the last example. First, let’s share the precept that every fraction has three signs, one on the numerator, one on the denominator, and a third on the fraction bar. Thus,
\[\frac{-2}{3} \quad \text { has understood signs } \quad+\frac{-2}{+3} \nonumber \]
Let’s state the sign change rule for fractions.
Every fraction has three signs, one on the numerator, one on the denominator, and one on the fraction bar. If you don’t see an explicit sign, then a plus sign is understood. If you negate any two of these parts,
- numerator and denominator, or
- numerator and fraction bar, or
- fraction bar and denominator,
then the fraction remains unchanged.
For example, let’s start with −2/3, then do two negations: numerator and fraction bar. Then,
\[+\frac{-2}{+3}=-\frac{+2}{+3}, \quad \text { or with understood plus signs, } \quad \frac{-2}{3}=-\frac{2}{3} \nonumber \]
This is a familiar result, as negative two divided by a positive three equals a negative two-thirds.
On another note, we might decide to negate numerator and denominator. Then −2/3 becomes
\[+\frac{-2}{+3}=\frac{+2}{-3}, \quad \text { or with understood plus signs, } \quad \frac{-2}{3}=\frac{2}{-3} \nonumber \]
Again, a familiar result. Certainly, negative two divided by positive three is the same as positive two divided by negative three. They both equal minus two-thirds.
So there you have it. Negate any two parts of a fraction and it remains unchanged. On the surface, this seems a trivial remark, but it can be put to good use when reducing rational expressions. Suppose, for example, that we take the original rational expression from Example \(\PageIndex{6}\) and negate the numerator and fraction bar.
\[\frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4}=-\frac{2 x^{3}-2 x}{3 x^{3}+4 x^{2}-3 x-4} \nonumber \]
Note how we’ve made two sign changes. We’ve negated the fraction bar, we’ve negated the numerator \(\left(-\left(2 x-2 x^{3}\right)=2 x^{3}-2 x\right)\), and left the denominator alone. Therefore, the fraction is unchanged according to our sign change rule.
Now, factor and cancel common factors (we leave the steps for our readers — they’re similar to those we took in Example \(\PageIndex{6}\)).
\[\begin{aligned} \frac{2 x-2 x^{3}}{3 x^{3}+4 x^{2}-3 x-4} &=-\frac{2 x^{3}-2 x}{3 x^{3}+4 x^{2}-3 x-4} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x(x+1)(x-1)}{(x+1)(x-1)(3 x+4)} \\ &=-\frac{2 x}{3 x+4} \end{aligned} \nonumber \]
But does this answer match the answer in equation (22)? It does, as can be seen by making two negations, fraction bar and numerator.
\[-\frac{2 x}{3 x+4}=\frac{-2 x}{3 x+4} \nonumber \]
The Secant Line
Consider the graph of the function f that we’ve drawn in Figure \(\PageIndex{3}\). Note that we’ve chosen two points on the graph of f, namely (a, f(a)) and (x, f(x)), and we’ve drawn a line L through them that mathematicians call the “secant line.”
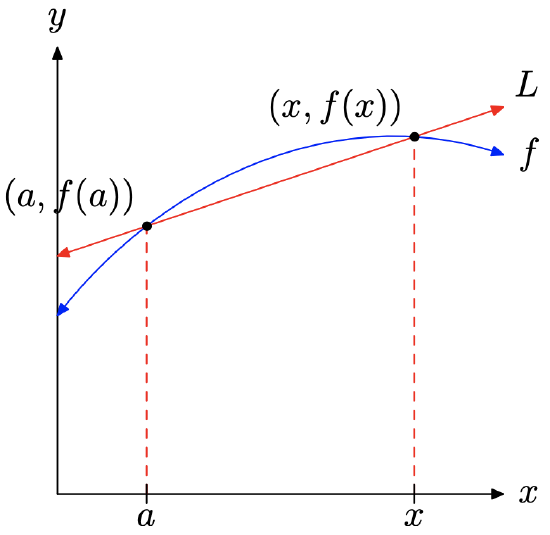
The slope of the secant line L is found by dividing the change in y by the change in x.
\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{f(x)-f(a)}{x-a} \nonumber \]
This slope provides the average rate of change of the variable y with respect to the variable x. Students in calculus use this “average rate of change” to develop the notion of “instantaneous rate of change.” However, we’ll leave that task for the calculus students and concentrate on the challenge of simplifying the expression equation (23) for the average rate of change.
Given the function \(f(x) = x^2\), simplify the expression for the average rate of change, namely \[\frac{f(x)-f(a)}{x-a} \nonumber \]
Solution
First, note that \(f(x)=x^{2}\) and \(f(a)=a^{2},\) so we can write \[\frac{f(x)-f(a)}{x-a}=\frac{x^{2}-a^{2}}{x-a} \nonumber \]
We can now use the difference of two squares pattern to factor the numerator and cancel common factors.
\[\frac{x^{2}-a^{2}}{x-a}=\frac{(x+a)(x-a)}{x-a}=x+a \nonumber \]
Thus, \[\frac{f(x)-f(a)}{x-a}=x+a \nonumber \]
provided, of course, that \(x \neq a\).
Let’s look at another example.
Consider the function \(f(x)=x^{2}-3 x-5\). Simplify \[\frac{f(x)-f(2)}{x-2} \nonumber \]
Solution
First, \(f(x)=x^{2}-3 x-5\) and therefore \(f(2)=(2)^{2}-3(2)-5=-7,\) so we can write
\[\frac{f(x)-f(2)}{x-2}=\frac{\left(x^{2}-3 x-5\right)-(-7)}{x-2}=\frac{x^{2}-3 x+2}{x-2} \nonumber \]
We can now factor the numerator and cancel common factors.
\[\frac{x^{2}-3 x+2}{x-2}=\frac{(x-2)(x-1)}{x-2}=x-1 \nonumber \]
Thus, \[\frac{f(x)-f(2)}{x-2}=x-1 \nonumber \] provided, of course, that \(x \neq 2\).
Exercise
In Exercises 1-12, reduce each rational number to lowest terms by applying the following steps:
- Prime factor both numerator and denominator.
- Cancel common prime factors.
- Simplify the numerator and denominator of the result.
\(\frac{147}{98}\)
- Answer
-
\(\frac{3}{2}\)
\(\frac{3087}{245}\)
\(\frac{1715}{196}\)
- Answer
-
\(\frac{35}{4}\)
\(\frac{225}{50}\)
\(\frac{1715}{441}\)
- Answer
-
\(\frac{35}{9}\)
\(\frac{56}{24}\)
\(\frac{108}{189}\)
- Answer
-
\(\frac{4}{7}\)
\(\frac{75}{500}\)
\(\frac{100}{28}\)
- Answer
-
\(\frac{25}{7}\)
\(\frac{98}{147}\)
\(\frac{1125}{175}\)
- Answer
-
\(\frac{45}{7}\)
\(\frac{3087}{8575}\)
In Exercises 13-18, reduce the given expression to lowest terms. State all restrictions.
\(\frac{x^2−10x+9}{5x−5}\)
- Answer
-
\(\frac{x−9}{5}\), provided \(x \ne 1\)
\(\frac{x^2−9x+20}{x^2−x−20}\)
\(\frac{x^2−2x−35}{x^2−7x}\)
- Answer
-
\(\frac{x+5}{x}\), provided \(x \ne 0, 7\)
\(\frac{x^2−15x+54}{x^2+7x−8}\)
\(\frac{x^2+2x−63}{x^2+13x+42}\)
- Answer
-
\(\frac{(x−7)(x+9)}{(x+7)(x+6)}\), provided \(x \ne −7, −6\)
\(\frac{x^2+13x+42}{9x+63}\)
In Exercises 19-24, negate any two parts of the fraction, then factor (if necessary) and cancel common factors to reduce the rational expression to lowest terms. State all restrictions.
\(\frac{x+2}{−x−2}\)
- Answer
-
−1, provided \(x \ne −2\)
\(\frac{4−x}{x−4}\)
\(\frac{2x−6}{3−x}\)
- Answer
-
−2, provided \(x \ne 3\)
\(\frac{3x+12}{−x−4}\)
\(\frac{3x^2+6x}{−x−2}\)
- Answer
-
−3x, provided \(x \ne −2\)
\(\frac{8x−2x^2}{x−4}\)
In Exercises 25-38, reduce each of the given rational expressions to lowest terms. State all restrictions.
\(\frac{x^2−x−20}{25−x^2}\)
- Answer
-
\(−\frac{x+4}{x+5}\), provided \(x \ne −5, 5\)
\(\frac{x−x^2}{x^2−3x+2}\)
\(\frac{x^2+3x−28}{x^2+5x−36}\)
- Answer
-
\(\frac{x+7}{x+9}\), provided \(x \ne 4, −9\)
\(\frac{x^2+10x+9}{x^2+15x+54}\)
\(\frac{x^2−x−56}{8x−x^2}\)
- Answer
-
\(−\frac{x+7}{x}\), provided \(x \ne 0, 8\)
\(\frac{x^2−7x+10}{5x−x^2}\)
\(\frac{x^2+13x+42}{x^2−2x−63}\)
- Answer
-
\(−\frac{x+6}{x−9}\), provided \(x \ne −7, 9\)
\(\frac{x^2−16}{x^2−x−12}\)
\(\frac{x^2−9x+14}{49−x^2}\)
- Answer
-
\(−\frac{x−2}{x+7}\), provided \(x \ne 7, −7\)
\(\frac{x^2+7x+12}{9−x^2}\)
\(\frac{x^2−3x−18}{x^2−6x+5}\)
- Answer
-
\(\frac{(x−6)(x+3)}{(x−1)(x−5)}\), provided \(x \ne 1, 5\)
\(\frac{x^2+5x−6}{x^2−1}\)
\(\frac{x^2−3x−10}{−9x−18}\)
- Answer
-
\(−\frac{x−5}{9}\), provided \(x \ne −2\)
\(\frac{x^2−6x+8}{16−x^2}\)
In Exercises 39-42, reduce each rational function to lowest terms, and then perform each of the following tasks.
- Load the original rational expression into Y1 and the reduced rational expression (your answer) into Y2 of your graphing calculator.
- In TABLE SETUP, set TblStart equal to zero, ∆Tbl equal to 1, then make sure both independent and dependent variables are set to Auto. Select TABLE and scroll with the up- and down-arrows on your calculator until the smallest restriction is in view. Copy both columns of the table onto your homework paper, showing the agreement between Y1 and Y2 and what happens at all restrictions.
\(\frac{x^2−8x+7}{x^2−11x+28}\)
- Answer
-
\(\frac{x−1}{x−4}\), provided \(x \ne 7, 4\)
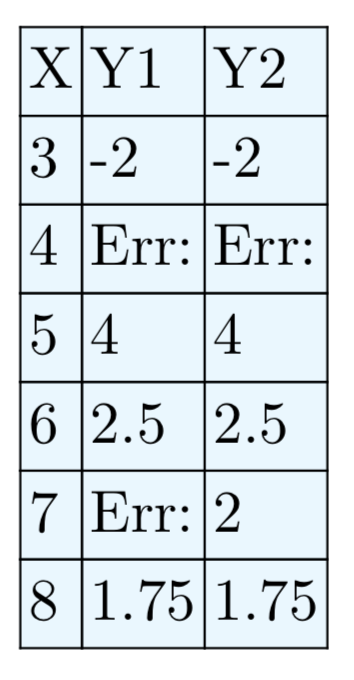
\(\frac{x^2−5x}{x^2−9x}\)
\(\frac{8x−x^2}{x^2−x−56}\)
- Answer
-
\(−\frac{x}{x+7}\), provided \(x \ne −7, 8\)
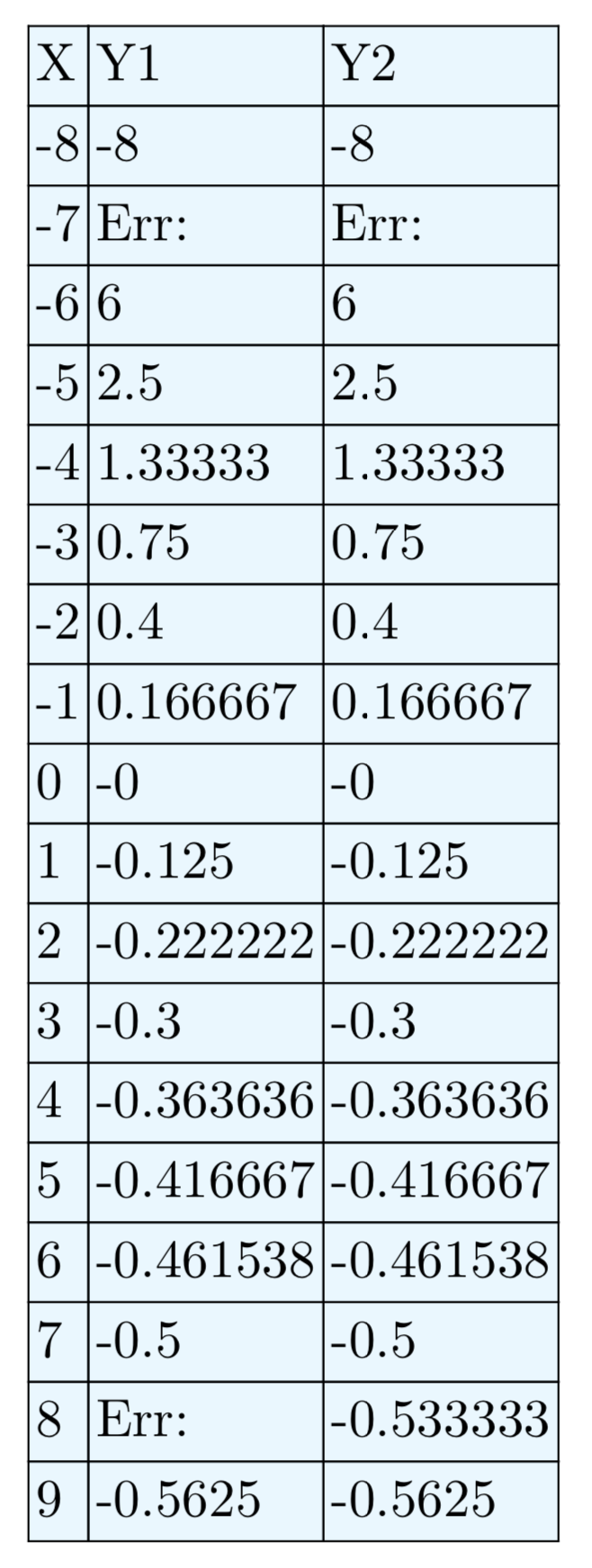
\(\frac{x^2+13x+40}{−2x−16}\)
Given f(x) = 2x+5, simplify each of the expressions in Exercises 43-46. Be sure to reduce your answer to lowest terms and state any restrictions.
\(\frac{f(x)−f(3)}{x−3}\)
- Answer
-
2, provided \(x \ne 3\)
\(\frac{f(x)−f(6)}{x−6}\)
\(\frac{f(x)−f(a)}{x−a}\)
- Answer
-
2, provided \(x \ne a\)
\(\frac{f(a+h)−f(a)}{h}\)
Given \(f(x) = x^2+2x\), simplify each of the expressions in Exercises 47-50. Be sure to reduce your answer to lowest terms and state any restrictions.
\(\frac{f(x)−f(1)}{x−1}\)
- Answer
-
x+3, provided \(x \ne 1\)
\(\frac{f(x)−f(a)}{x−a}\)
\(\frac{f(a+h)−f(a)}{h}\)
- Answer
-
2a+h+2, provided \(h \ne 0\)
\(\frac{f(x+h)−f(x)}{h}\)
Drill for Skill. In Exercises 51-54, evaluate the given function at the given expression and simplify your answer.
Suppose that f is the function
\(f(x) = −\frac{x−6}{8x+7}\)
Evaluate f(−3x+2) and simplify your answer.
- Answer
-
\(−\frac{3x+4}{24x−23}\)
Suppose that f is the function
\(f(x) = −\frac{5x+3}{7x+6}\)
Evaluate f(−5x+1) and simplify your answer.
Suppose that f is the function
\(f(x) = −\frac{3x−6}{4x+6}\)
Evaluate f(−x−3) and simplify your answer.
- Answer
-
\(−\frac{3x+15}{4x+6}\)
Suppose that f is the function
\(f(x) = \frac{4x−1}{2x−4}\)
Evaluate f(5x) and simplify your answer.


