11.5E: Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Practice Makes Perfect
In the following exercises, graph.
- x29−y24=1
- x225−y29=1
- x216−y225=1
- x29−y236=1
- y225−x24=1
- y236−x216=1
- 16y2−9x2=144
- 25y2−9x2=225
- 4y2−9x2=36
- 16y2−25x2=400
- 4x2−16y2=64
- 9x2−4y2=36
- Answer
-
1.
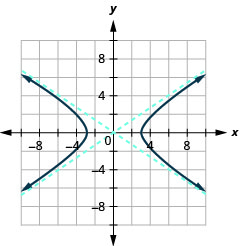
Figure 11.4.33 3.
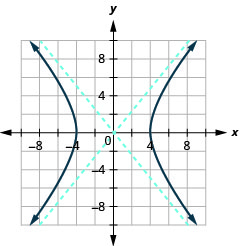
Figure 11.4.34 5.
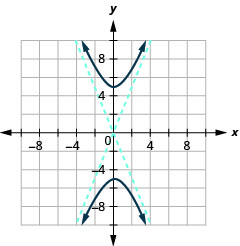
Figure 11.4.35 7.
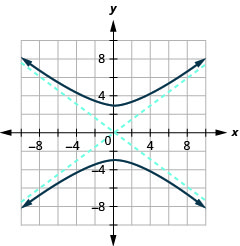
Figure 11.4.36 9.
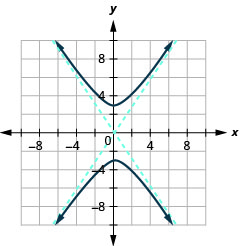
Figure 11.4.37 11.
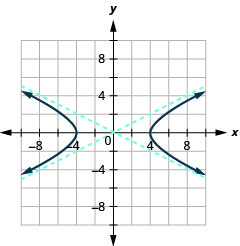
Figure 11.4.38
In the following exercises, graph.
- (x−1)216−(y−3)24=1
- (x−2)24−(y−3)216=1
- (y−4)29−(x−2)225=1
- (y−1)225−(x−4)216=1
- (y+4)225−(x+1)236=1
- (y+1)216−(x+1)24=1
- (y−4)216−(x+1)225=1
- (y+3)216−(x−3)236=1
- (x−3)225−(y+2)29=1
- (x+2)24−(y−1)29=1
- Answer
-
1.
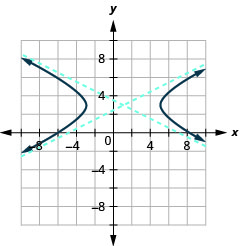
Figure 11.4.39 3.
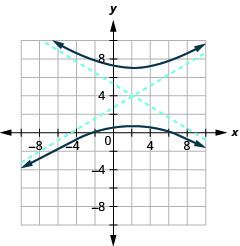
Figure 11.4.40 5.
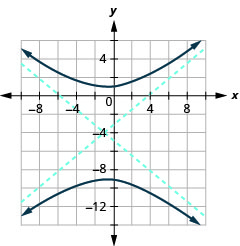
Figure 11.4.41 7.
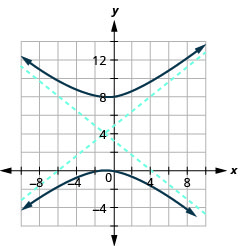
Figure 11.4.42 9.
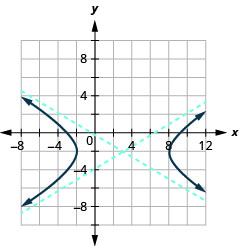
Figure 11.4.43
In the following exercises,
- Write the equation in standard form and
- Graph.
- 9x2−4y2−18x+8y−31=0
- 16x2−4y2+64x−24y−36=0
- y2−x2−4y+2x−6=0
- 4y2−16x2−24y+96x−172=0
- 9y2−x2+18y−4x−4=0
- Answer
-
1.
- (x−1)24−(y−1)29=1
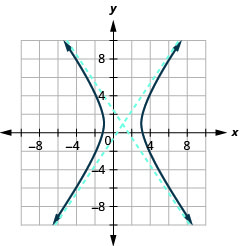
Figure 11.4.44 3.
- (y−2)29−(x−1)29=1
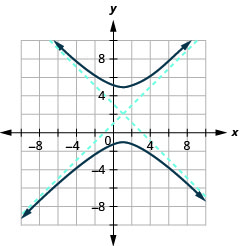
Figure 11.4.45 5.
- (y+1)21−(x+2)29=1
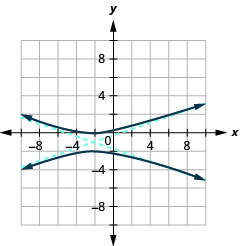
Figure 11.4.46
In the following exercises, identify the type of graph.
-
- x=−y2−2y+3
- 9y2−x2+18y−4x−4=0
- 9x2+25y2=225
- x2+y2−4x+10y−7=0
-
- x=−2y2−12y−16
- x2+y2=9
- 16x2−4y2+64x−24y−36=0
- 16x2+36y2=576
- Answer
-
2.
- Parabola
- Circle
- Hyperbola
- Ellipse
In the following exercises, graph each equation.
- (y−3)29−(x+2)216=1
- x2+y2−4x+10y−7=0
- y=(x−1)2+2
- x29+y225=1
- (x+2)2+(y−5)2=4
- 9x2−4y2+54x+8y+41=0
- x=−y2−2y+3
- 16x2+9y2=144
- Answer
-
2.
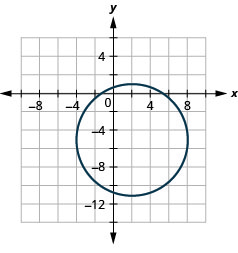
Figure 11.4.47 4.
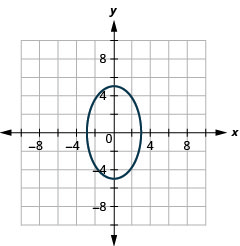
Figure 11.4.48 6.
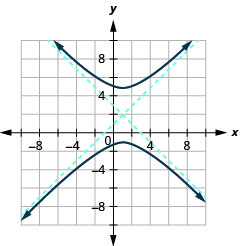
Figure 11.4.49 8.
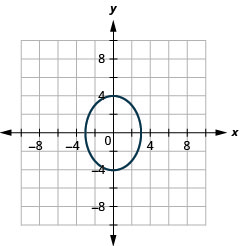
Figure 11.4.50
- In your own words, define a hyperbola and write the equation of a hyperbola centered at the origin in standard form. Draw a sketch of the hyperbola labeling the center, vertices, and asymptotes.
- Explain in your own words how to create and use the rectangle that helps graph a hyperbola.
- Compare and contrast the graphs of the equations x24−y29=1 and y29−x24=1.
- Explain in your own words, how to distinguish the equation of an ellipse with the equation of a hyperbola.
- Answer
-
2. Answers may vary
4. Answers may vary
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?


