12.2: Exponential functions
- Page ID
- 45118
Exponential functions take on their own set of solving and simplifying techniques since the equations are a bit different than before. For example, before we had something like \(x^2 = 9\), where we could take square root of each side to solve. However, if we had something like \(3^x = 9\), notice we cannot take the \(x^{\text{th}}\) root of \(9\) because the index is unknown. However, we may notice that \(3^2 = 9\) and conclude that if \(3^x = 3^2\), then \(x = 2\). This is a simple example, but what if we had something a little more complex, like \(10.98564^x = 34.9016\)? Then the value of \(x\) isn’t as obvious. These are the cases we address in this section and chapter.
One common application of exponential functions is population growth. According to the 2009 CIA World Factbook, the country with the highest population growth rate is tied between the United Arab Emirates (north of Saudi Arabia) and Burundi (central Africa) at \(3.69\%\). There are \(32\) countries with negative growth rates, the lowest being the Northern Mariana Islands (north of Australia) at \(−7.08\%\).
An exponential function is a function of the form
\[f(x) = a^x,\nonumber\]
where \(f\) is a function of \(x\), \(a > 0\) and \(a\neq 1\).
Graph Exponential Functions
Let’s start to take a look at exponential functions by looking at their graphs.
Plot \(f(x) = 3^x\) by plotting points. From the graph, determine the domain of the function.
Solution
Let’s pick five \(x\)-coordinates, and find corresponding \(y\)-values. Each \(x\)-value being positive or negative, and zero. This is common practice, but not required.
| \(x\) | \(f(x)=3^x\) | \((x,f(x))\) |
|---|---|---|
| \(-2\) | \(f(\color{blue}{-2}\color{black}{)}=3^{\color{blue}{-2}}\color{black}{=}\dfrac{1}{9}\) | \(\left(-2,\dfrac{1}{9}\right)\) |
| \(-1\) | \(f(\color{blue}{-1}\color{black}{)}=3^{\color{blue}{-1}}\color{black}{=}\dfrac{1}{3}\) | \(\left(-1,\dfrac{1}{3}\right)\) |
| \(0\) | \(f(\color{blue}{0}\color{black}{)}=3^{\color{blue}{0}}\color{black}{=}1\) | \((0,1)\) |
| \(1\) | \(f(\color{blue}{1}\color{black}{)}=3^{\color{blue}{1}}\color{black}{=}3\) | \((1,3)\) |
| \(2\) | \(f(\color{blue}{2}\color{black}{)}=3^{\color{blue}{2}}\color{black}{=}9\) | \((2,9)\) |
Plot the five ordered-pairs from the table. To connect the points, be sure to connect them from smallest \(x\)-value to largest \(x\)-value, i.e., left to right. Notice this graph is rising left to right, but, as the graph shoots to \(−∞\) (to the left), it never touches the \(x\)-axis or intersects it, resulting in a horizontal asymptote at \(y = 0\). Since we see there are no restrictions to the graph, the domain is all real numbers or \((−∞, ∞)\).
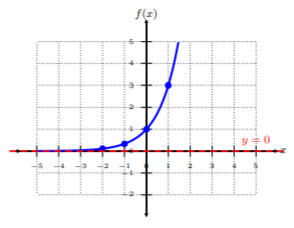
Property 1. The domain of an exponential function is all real numbers, i.e., \((−∞, ∞)\).
Property 2. There are no \(x\)-intercepts; the \(y\)-intercept is at \((0, 1)\).
Property 3. If \(a > 1\), then the function is an increasing function. If \(0 < a < 1\), then the function is a decreasing function.
Property 4. There is a horizontal asymptote at \(y = 0\), unless there is a vertical shift.
An exponential function never crosses the \(x\)-axis. In fact, the general exponential function isn’t defined at \(f(x) = 0\). Take a look. If \(f(x) = 0\), then \(f(x) = 0 = a^x\). Ask, “For which value(s) of \(x\) such that a is raised to the power of \(x\) and the result is zero?” There exists no such \(x\). We cannot raise a positive real number to a power and the result be zero. In the event an exponential function crosses the \(x\)-axis, then that means there was a transformation to the general exponential function.
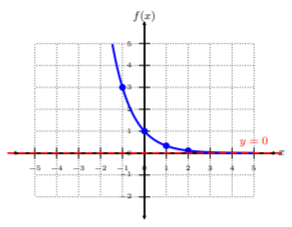
Plot \(f(x)=\left(\dfrac{1}{3}\right)^x\) by plotting points. From the graph, determine the domain of the function.
Solution
Let’s pick five \(x\)-coordinates, and find corresponding \(y\)-values. Each \(x\)-value being positive or negative, and zero. This is common practice, but not required.
| \(x\) | \(f(x)=\dfrac{1}{3}^x\) | \((x,f(x))\) |
|---|---|---|
| \(-2\) | \(f(\color{blue}{-2}\color{black}{)}=\left(\dfrac{1}{3}\right)^{\color{blue}{-2}}\color{black}{=}9\) | \((-2,9)\) |
| \(-1\) | \(f(\color{blue}{-1}\color{black}{)}=\left(\dfrac{1}{3}\right)^{\color{blue}{-1}}\color{black}{=}3\) | \((-1,3)\) |
| \(0\) | \(f(\color{blue}{0}\color{black}{)}=\left(\dfrac{1}{3}\right)^{\color{blue}{0}}\color{black}{=}1\) | \((0,1)\) |
| \(1\) | \(f(\color{blue}{1}\color{black}{)}=\left(\dfrac{1}{3}\right)^{\color{blue}{1}}\color{black}{=}\dfrac{1}{3}\) | \(\left(1,\dfrac{1}{3}\right)\) |
| \(2\) | \(f(\color{blue}{2}\color{black}{)}=\left(\dfrac{1}{3}\right)^{\color{blue}{2}}\color{black}{=}\dfrac{1}{9}\) | \(\left(2,\dfrac{1}{9}\right)\) |
Plot the five ordered-pairs from the table. To connect the points, be sure to connect them from smallest \(x\)-value to largest \(x\)-value, i.e., left to right. Notice this graph is falling left to right, but, as the graph shoots to \(∞\) (to the right), it never touches the \(x\)-axis or intersects it. Since we see there are no restrictions to the graph, the domain is all real numbers or \((−∞, ∞)\), and there is a horizontal asymptote at \(y = 0\).
Exponential Equations with a Common Base
Since the exponential function is one-to-one, we get the following.
To solve an exponential equation with a common base on each side of the equation, we use the fact that if
\[a^m=a^n,\text{ then }m=n.\nonumber\]
Solve the equation: \(5^{2x+1}=125\)
Solution
We use the fact above to solve the equation.
\[\begin{array}{rl} 5^{2x+1}=125 & \text{Rewrite }125\text{ as }5^3 \\ 5^{\color{blue}{2x+1}}\color{black}{=}5^{\color{blue}{3}} & \text{Common base, equate exponents} \\ \color{blue}{2x+1}\color{black}{=}\color{blue}{3} & \text{Solve for }x \\ 2x=2 & \text{Divide both sides by }2 \\ x=1 & \text{Solution}\end{array}\nonumber\]
We can always check the answer by verifying the solution.
\[\begin{aligned} 5^{2x+1}&\stackrel{?}{=}125\quad\text{Plug-n-chug }x=1 \\ 5^{2(\color{blue}{1}\color{black}{)}+1}&\stackrel{?}{=}125\quad\text{Simplify the left side} \\ 5^3&\stackrel{?}{=}125\quad\text{Evaluate }5^3 \\ 125&=125 \quad\checkmark \text{ True} \end{aligned}\]
Since we obtain a true statement by verifying the solution, then \(x = 1\) is the solution.
Solve the equation: \(8^{3x}=32\)
Solution
In this case, it may not seem as obvious at first, but if we rewrite each base as a common base, then we can apply the fact. Let’s rewrite each base as a common base of \(2\).
\[\begin{array} {rl} 8^{3x}=32 & \text{Rewrite }8\text{ as }2^3\text{ and }32\text{ as }2^5 \\ (2^3)^{3x}=2^5 & \text{Multiply exponents }3\text{ and }3x \\ 2^{\color{blue}{9x}} \color{black}{=}2^{\color{blue}{5}} & \text{Common base, equate exponents} \\ \color{blue}{9x}\color{black}{=}\color{blue}{5} & \text{Solve for }x \\ x=\dfrac{5}{9} & \text{Solution}\end{array}\nonumber \]
We can always verify the solution, but we leave this to the student.
Solve the equation: \(\left(\dfrac{1}{9}\right)^{2x}=3^{7x-1}\)
Solution
In this case, it may not seem as obvious at first, but if we rewrite each base as a common base, then we can apply the fact. Let’s rewrite each base as a common base of \(3\).
\[\begin{array} {rl} \left(\dfrac{1}{9}\right)^{2x}=3^{7x-1} & \text{Rewrite }\dfrac{1}{9}\text{ as }\dfrac{1}{3^2} \\ \left(\dfrac{1}{3^2}\right)^{2x}=3^{7x-1} & \text{Rewrite }\dfrac{1}{3^2}\text{ as }3^{-2} \\ (3^{-2})^{2x}=3^{7x-1} & \text{Multiply exponents }-2\text{ and }2x \\ 3^{\color{blue}{-4x}}\color{black}{=}3^{\color{blue}{7x-1}} & \text{Common base, equate exponents} \\ \color{blue}{-4x}\color{black}{=}\color{blue}{7x-1} & \text{Solve} \\ -11x=-1 & \text{Isolate }x \\ x=\dfrac{1}{11}& \text{Solution}\end{array}\nonumber \]
We can always verify the solution, but we leave this to the student.
Solve the equation: \(5^{4x}\cdot 5^{2x−1} = 5^{3x+11}\)
Solution
In this case, it may not seem as obvious at first, but we need to apply the product rule of exponents and obtain only one common base on each side of the equation in order to apply the fact.
\[\begin{array}{rl} 5^{4x}\cdot 5^{2x-1}=5^{3x+11} & \text{Apply product rule of exponents on the left side} \\ 5^{4x+2x-1}=5^{3x+11}& \text{Simplify the exponent on the left side} \\ 5^{\color{blue}{6x-1}}\color{black}{=}5^{\color{blue}{3x+11}} & \text{Common base, equate exponents} \\ \color{blue}{6x-1}\color{black}{=}\color{blue}{3x+11} & \text{Combine like terms} \\ 3x=12 & \text{Isolate }x \\ x=4& \text{Solution}\end{array}\nonumber\]
We can always verify the solution, but we leave this to the student.
Notice, the examples only present a technique for solving exponential equations with a common base. However, not all exponential equations are written with a common base. For example, something like \(2 = 10^x\) cannot be written with a common base. To solve problems where we cannot rewrite the bases with a common base, we need the logarithmic function, which we will discuss in the next section.
Exponential Functions Homework
Graph each exponential function.
\(f(x)=4^x\)
\(x(y)=\left(\dfrac{1}{4}\right)^y\)
\(f(x)=-3^x\)
\(q(r)=-\left(\dfrac{1}{5}\right)^r\)
\(h(n)=\left(\dfrac{1}{2}\right)^n\)
\(g(x)=2^x\)
\(j(x)=-2^x\)
\(k(t)=-\left(\dfrac{1}{2}\right)^t\)
Solve the equation.
\(3^{1-2n}=3^{1-3n}\)
\(4^{2a}=1\)
\(\left(\dfrac{1}{25}\right)^{-k}=125^{-2k-2}\)
\(6^{2m+1}=\dfrac{1}{36}\)
\(6^{-3x}=36\)
\(64^b=2^5\)
\(\left(\dfrac{1}{4}\right)^x=16\)
\(4^{3a}=4^3\)
\(36^{3x}=216^{2x+1}\)
\(9^{2n+1}=243\)
\(3^{3x-2}=3^{3x+1}\)
\(3^{-2x}=3^3\)
\(5^{m+2}=5^{-m}\)
\(\left(\dfrac{1}{36}\right)^{b-1}=216\)
\(6^{2-2x}=6^2\)
\(4\cdot 2^{-3n-1}=\dfrac{1}{4}\)
\(4^{3k-3}\cdot 4^{2-2k}=16^{-k}\)
\(9^{-2x}\cdot\left(\dfrac{1}{243}\right)^{3x}=243^{-x}\)
\(64^{n-2}\cdot 16^{n+2}=\left(\dfrac{1}{4}\right)^{3n-1}\)
\(5^{-3n-3}\cdot 5^{2n}=1\)
\(4^{2x}=\dfrac{1}{16}\)
\(16^{-3p}=64^{-3p}\)
\(625^{-n-2}=\dfrac{1}{125}\)
\(6^{2r-3}=6^{r-3}\)
\(5^{2n}=5^{-n}\)
\(216^{-3v}=36^{3v}\)
\(27^{-2n-1}=9\)
\(4^{-3v}=64\)
\(64^{x+2}=16\)
\(16^{2k}=\dfrac{1}{64}\)
\(243^{p}=27^{-3p}\)
\(4^{2n}=4^{2-3n}\)
\(625^{2x}=25\)
\(216^{2n}=36\)
\(\left(\dfrac{1}{4}\right)^{3v-2}=64^{1-v}\)
\(\dfrac{216}{6^{-2a}}=6^{3a}\)
\(32^{2p-2}\cdot 8^p=\left(\dfrac{1}{2}\right)^{2p}\)
\(3^{2m}\cdot 3^{3m}=1\)
\(3^{2-x}\cdot 3^{3x}=1\)
\(4^{3r}\cdot 4^{-3r}=\dfrac{1}{64}\)