12.3: Logarithmic functions
- Page ID
- 45119
Inverse functions of exponential functions are logarithmic functions, i.e., if we were to compose a logarithmic function with an exponential function (or vice versa) and the result is \(x((f\circ g)(x)=x\), then the logarithmic and exponential functions are inverses of each other. The study of logarithms is particularly interesting in many aspects of algebra, and even in advanced algebra, because they are one of the most useful functions. In this section, we introduce logarithms.
The logarithmic function is denoted by
\[y = \log_{a} x\text{ which is equivalent to }x = a^y,\nonumber\]
where \(a > 0\) and \(a\neq 1\). The base is \(a,\: y\) is the exponent, and \(x\) is the value.
The equation \(y = \log_a x\) is called the logarithmic form and \(x = a^y\) is called the exponential form.
When we rewrite equations in logarithmic and exponential form, we can look at the equations in a more general way so that it is obvious where we place parameters:
\[\color{blue}{\text{exponent}}\color{black}{=}\log_{\color{red}{\text{base}}}\color{GreenYellow}{\text{value}}\color{black}{\quad}which\: is\: equivalent\: to\quad\color{GreenYellow}{\text{value}}\color{black}{=}\color{red}{\text{base}}^{\color{blue}{\text{exponent}}}\nonumber\]
Write in Logarithmic and Exponential Form
Write each exponential equation in its equivalent logarithmic form.
- \(m^3=5\)
- \(7^2=b\)
- \(\left(\dfrac{2}{3}\right)^4=\dfrac{16}{81}\)
Solution
We first begin to identify the base, exponent and value. Then we rewrite the equation in logarithmic form.
- In the equation \(m^3 = 5\), we identify \(m\) is the base, \(3\) is the exponent, and \(5\) is the value.
\[\color{blue}{3}\color{black}{=}\log_{\color{red}{m}}\color{GreenYellow}{5}\color{black}{\quad} which\: is\: equivalent\: to\quad\color{GreenYellow}{5}\color{black}{=}\color{red}{m}^{\color{blue}{3}}\nonumber\] - In the equation \(7^2 = b\), we identify \(7\) is the base, \(2\) is the exponent, and \(b\) is the value.
\[\color{blue}{2}\color{black}{=}\log_{\color{red}{7}}\color{GreenYellow}{b}\color{black}{\quad} which\: is\: equivalent\: to\quad\color{GreenYellow}{b}\color{black}{=}\color{red}{7}^{\color{blue}{2}}\nonumber\] - In the equation \(\left(\dfrac{2}{3}\right)^4=\dfrac{16}{81}\), we identify \(\dfrac{2}{3}\) is the base, \(4\) is the exponent, and \(\dfrac{16}{81}\) is the value.
\[\color{blue}{4}\color{black}{=}\log_{\color{red}{\dfrac{2}{3}}}\color{GreenYellow}{\dfrac{16}{81}}\color{black}{\quad} which\: is\: equivalent\: to\quad\color{GreenYellow}{\dfrac{16}{81}}\color{black}{=}\color{red}{\left(\dfrac{2}{3}\right)}^{\color{blue}{4}}\nonumber\]
Write each logarithmic equation in its equivalent exponential form
- \(\log_x 16=2\)
- \(\log_3 x=7\)
- \(\log_9 3=x\)
Solution
We first begin to identify the base, exponent and value. Then we rewrite the equation in exponential form.
- In the equation \(\log_x 16 = 2\), we identify \(x\) is the base, \(2\) is the exponent, and \(16\) is the value.
\[\color{GreenYellow}{16}\color{black}{=}\color{red}{x}^{\color{blue}{2}}\color{black}{\quad}which\: is\: equivalent\: to\quad\color{blue}{2}\color{black}{=}\log_{\color{red}{x}}\color{GreenYellow}{16}\nonumber\] - In the equation \(\log_3 x = 7\), we identify \(3\) is the base, \(7\) is the exponent, and \(x\) is the value.
\[\color{GreenYellow}{x}\color{black}{=}\color{red}{3}^{\color{blue}{7}}\color{black}{\quad}which\: is\: equivalent\: to\quad\color{blue}{7}\color{black}{=}\log_{\color{red}{3}}\color{GreenYellow}{x}\nonumber\] - In the equation \(\log_9 3 = x\), we identify \(9\) is the base, \(x\) is the exponent, and \(3\) is the value.
\[\color{GreenYellow}{3}\color{black}{=}\color{red}{9}^{\color{blue}{x}}\color{black}{\quad}which\: is\: equivalent\: to\quad\color{blue}{x}\color{black}{=}\log_{\color{red}{9}}\color{GreenYellow}{3}\nonumber\]
Evaluate Logarithmic Functions
Since logarithms are just exponents, then we can use logarithms to find the exponent, or one of the other parameters, the base or value.
Find the exact value: \(\log_5 125\)
Solution
To find the exact value, we refrain from using any technology to obtain the answer and we only use the definition of a logarithmic function. Hence, when we see the expression \(\log_5 125\), we ask, “\(5\) to what power is \(125\)?” because, recall, logarithms are just exponents. Some might already see the answer is \(3\), but let’s use the definition to present a method for evaluating logarithms. Let \(\log_5 125 = x\).
\[\begin{array}{rl} \log_5 125=x & \text{Rewrite in exponential form} \\ 5^x=125 & \text{Rewrite using common base }5 \\ 5^x=5^3 & \text{Common base, equate exponents} \\ x=3 & \text{Solution}\end{array}\nonumber\]
We need to be careful because we introduced \(x\), but \(x\) was never part of the original problem. Thus, let’s write the answer properly.
\[\log_5 125=3\nonumber\]
Find the exact value: \(\log_3 \dfrac{1}{27}\)
Solution
To find the exact value, we refrain from using any technology to obtain the answer and we only use the definition of a logarithmic function. Hence, when we see the expression \(\log_3 \dfrac{1}{27}\), we ask, “\(3\) to what power is \(\dfrac{1}{27}\)?” because, recall, logarithms are just exponents. Let \(\log_3 \dfrac{1}{27}=x\).
\[\begin{array}{rl} \log_3\dfrac{1}{27}=x & \text{Rewrite in exponential form} \\ 3^x=\dfrac{1}{27} & \text{Rewrite using common base }3 \\ 3^x=\dfrac{1}{3^3} & \text{Rewrite using negative exponent }-3 \\ 3^x=3^{-3} & \text{Common base, equate exponents} \\ x=-3 & \text{Solution}\end{array}\nonumber\]
We need to be careful because we introduced \(x\), but \(x\) was never part of the original problem. Thus, let’s write the answer properly.
\[\log_3\dfrac{1}{27}=-3\nonumber\]
Domain of Logarithmic Functions
Recall. The domain of a function is the interval of independent values defined for that function.
Hence, it makes sense to discuss the domain of logarithmic functions. With exponential functions, the domain is all real numbers, but let’s see the way it differs from the domain of a logarithmic function.
The domain of the logarithmic function is \(\{x|x > 0\}\) or \((0, ∞)\), i.e., the value (or argument) of the logarithm is always positive.
Given the logarithmic function \(f(x) = \log_a x\), we can follow the steps below to obtain the domain.
Step 1. Identify the value of the logarithm, \(x\). The value will differ from \(x\) as the problems change.
Step 2. Set the value greater than zero, i.e., \(x > 0\).
Step 3. Solve the inequality as usual.
Step 4. Rewrite the inequality in interval notation, if needed.
Find the domain of \(f(x)=\log_5 (2x+3)\).
Solution
We can follow the steps to obtain the domain of \(f(x)\).
Step 1. The value of the given logarithm is \((2x + 3)\).
Step 2. Setting the value greater than zero, we get \(2x + 3 > 0\).
Step 3. Solving the inequality as usual,
\[\begin{aligned}2x+3&>0 \\ 2x&>-3 \\ x&>-\dfrac{3}{2}\end{aligned}\]
This means that all values for \(x\) are required to be strictly greater than \(-\dfrac{3}{2}\) in order for \(f(x)\) to be defined.
Step 4. Rewriting \(-\dfrac{3}{2}\) in interval notation, we get \(\left(-\dfrac{3}{2},\infty\right)\).
Thus, the domain of \(f(x)\) is \(\left\{x\mid x>-\dfrac{3}{2}\right\}\) or, equivalently, \(\left(-\dfrac{3}{2},\infty\right)\).
Graph Logarithmic Functions
Let’s start to take a look at logarithmic functions by looking at their graphs. Recall, logarithmic and exponential functions are inverses of each other. Hence, we’ll see that their properties also invert, i.e., \(x\) and \(y\) coordinates switch.
Plot \(f(x) = \log_3 x\) by plotting points. From the graph, determine the domain of the function.
Solution
Let’s rewrite the function as \(y = \log_3 x\), and then in its equivalent exponential form: \(3^y = x\). Looking at the exponential form of \(f(x)\), we choose to pick \(y\)-coordinates, and find corresponding \(x\)-values. In choosing \(y\) coordinates, we can evaluate the exponential form easily.
| \(y\) | \(3^y=x\) | \((x,f(x))\) |
|---|---|---|
| \(-2\) | \(3^{\color{blue}{-2}}\color{black}{=}\dfrac{1}{9}\) | \(\left(\dfrac{1}{9},-2\right)\) |
| \(-1\) | \(3^{\color{blue}{-1}}\color{black}{=}\dfrac{1}{3}\) | \(\left(\dfrac{1}{3},-1\right)\) |
| \(0\) | \(3^{\color{blue}{0}}\color{black}{=}1\) | \((1,0)\) |
| \(1\) | \(3^{\color{blue}{1}}\color{black}{=}3\) | \((3,1)\) |
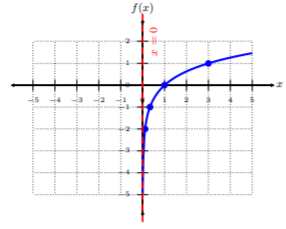
Plot the five ordered-pairs from the table. To connect the points, be sure to connect them from smallest \(x\)-value to largest \(x\)-value, i.e., left to right. Notice this graph is rising left to right, but, as the graph shoots towards \(0\), it never touches the \(y\)-axis or intersects it, resulting in a vertical asymptote, \(x = 0\). Since we see there is one restriction to the graph, the domain is all real numbers greater than zero or \((0, ∞)\).
Property 1. The domain of an logarithmic function is all real numbers greater than zero, i.e., \((0, ∞)\).
Property 2. There are no \(y\)-intercepts; the \(x\)-intercept is at \((1, 0)\).
Property 3. If \(a > 1\), then the function is an increasing function. If \(0 < a < 1\), then the function is a decreasing function.
Property 4. There is a vertical asymptote at \(x = 0\), unless there is a horizontal shift.
A logarithmic function never crosses the \(y\)-axis. In fact, the general logarithmic function isn’t defined at \(x = 0\). Take a look. If \(x = 0\), then \(f(0) = \log_a 0\). Ask, “\(a\) to what power is zero?” There exists no such power. We cannot raise a positive real number to a power and the result be zero. In the event a logarithmic function crosses the \(y\)-axis, then that means there was a transformation to the general logarithmic function.
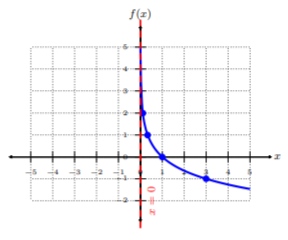
Plot \(f(x) = \log_{1/3} x\) by plotting points. From the graph, determine the domain of the function.
Solution
Let’s rewrite the function as \(y = \log_{1/3} x\), and then in its equivalent exponential form: \(\left(\dfrac{1}{3}\right)^{y}=x\). Looking at the exponential form of \(f(x)\), we choose to pick \(y\)-coordinates, and find corresponding \(x\)-values. In choosing \(y\) coordinates, we can evaluate the exponential form easily.
| \(x\) | \(\dfrac{1}{3}^y=x\) | \((x,f(x))\) |
|---|---|---|
| \(-1\) | \(\left(\dfrac{1}{3}\right)^{\color{blue}{-1}}\color{black}{=}3\) | \((3,-1)\) |
| \(0\) | \(\left(\dfrac{1}{3}\right)^{\color{blue}{0}}\color{black}{=}1\) | \((1,0)\) |
| \(1\) | \(\left(\dfrac{1}{3}\right)^{\color{blue}{1}}\color{black}{=}\dfrac{1}{3}\) | \(\left(\dfrac{1}{3},1\right)\) |
| \(2\) | \(\left(\dfrac{1}{3}\right)^{\color{blue}{2}}\color{black}{=}\dfrac{1}{9}\) | \(\left(\dfrac{1}{9},2\right)\) |
Plot the five ordered-pairs from the table. To connect the points, be sure to connect them from smallest \(x\)-value to largest \(x\)-value, i.e., left to right. Notice this graph is falling left to right, but, as the graph shoots towards \(0\), it never touches the \(y\)-axis or intersects it, resulting in a horizontal asymptote at \(x = 0\). Since we see there is one restriction to the graph, the domain is all real numbers greater than zero or \((0, ∞)\).
This is a good time to mention two very important logarithms: the natural and common logarithm.
- The natural logarithm is given by
\[y = \log_e x = \ln x\text{ if and only if }x = e^y\nonumber\]
where \(e\) is the irrational number Euler’s constant, \(e\approx 2.71828182\cdots\) Notice the \(\log_e\) is replaced with \(\ln\), and that is the only difference. - The common logarithm is given by
\[y = \log_{10} x = \log x\text{ if and only if }x = 10^y\nonumber\]
Notice the \(\log_{10}\) is replaced with \(\log\), and that is the only difference. When there is no written base on the logarithm, then it is assumed it is the common logarithm (unless it is \(\ln\)).
Dutch mathematician Adriaan Vlacq published a textbook in 1628 which listed logarithms calculated out from \(1\) to \(100,000\).
Solve Logarithmic Equations
Solving equations with logarithms has techniques that are similar when solving exponential equations. We can rewrite the logarithmic equation in its equivalent exponential form and solve.
Solve for \(x:\:\log_5 x=2\)
Solution
We solve the equation by rewriting the equation in its equivalent exponential form and solve.
\[\begin{aligned}\log_5 x&=2\quad\text{Rewrite in exponential form} \\ 5^2&=x\quad\text{Simplify} \\ 25&=x\quad\text{Solution}\end{aligned}\]
Solve for \(n:\:\log_2(3n+5)=4\)
Solution
We solve the equation by rewriting the equation in its equivalent exponential form and solve.
\[\begin{array}{rl}\log_2(3n+5)=4 & \text{Rewrite in exponential form} \\ 2^4=3n+5 & \text{Simplify }2^4 \\ 16=3n+5 & \text{Isolate the variable term} \\ 11=3n & \text{Isolate }n \\ \dfrac{11}{3}=n & \text{Solution}\end{array}\nonumber\]
We can see that the technique is, once the logarithm is isolated on one side of the equation, we can rewrite the equation in its equivalent exponential form and solve.
Solve for \(t:\: \log(2t-3)=-1\)
Solution
We solve the equation by rewriting the equation in its equivalent exponential form and solve. First, we see that there is no written base on the logarithm. Hence, we assume this is a common logarithm and the base is ten.
\[\begin{array}{rl} \log(2t-3)=-1 & \text{Write the common logarithm with a base }10 \\ \log_{10}(2t-3)=-1 & \text{Rewrite in exponential form} \\ 10^{-1}=2t-3 & \text{Simplify }10^{-1} \\ \dfrac{1}{10}=2t-3 & \text{Isolate the variable term} \\ \dfrac{31}{10}=2t & \text{Isolate }t \\ \dfrac{1}{2}\cdot\dfrac{31}{10}=t & \text{Simplify the left side} \\ \dfrac{31}{20}=t & \text{Solution}\end{array}\nonumber\]
Solve for \(a:\:\ln a=4\)
Solution
We solve the equation by rewriting the equation in its equivalent exponential form and solve. First, we see ln and assume this is a natural logarithm and the base is \(e\).
\[\begin{array}{rl} \ln a=4 &\text{Write the natural logarithm with a base }e \\ \log_e a=4 &\text{Rewrite in exponential form} \\ e^4=a &\text{Solution} \\ 54.598\approx a &\text{Approximate solution for }a\end{array}\nonumber\]
Logarithmic Functions Homework
Rewrite each equation in exponential form.
\(\log_9 81=2\)
\(\log_7\dfrac{1}{49}=-2\)
\(\log_{13}169=2\)
\(\log_b a=-16\)
\(\log_{16}256 =2\)
\(\log_{11}1=0\)
Rewrite each equation in logarithmic form.
\(8^0=1\)
\(15^2=225\)
\(64^{1/6}=2\)
\(17^{-2}=\dfrac{1}{289}\)
\(144^{1/2}=12\)
\(19^2=361\)
Find the exact value for each expression.
\(\log_{125}5\)
\(\log_{343}\dfrac{1}{7}\)
\(\log_{4}16\)
\(\log_{6}36\)
\(\log_{2}64\)
\(\log_{5}125\)
\(\log_{7}1\)
\(\log_{4}\dfrac{1}{64}\)
\(\log_{36}6\)
\(\log_{3}243\)
Find the domain of each logarithmic function.
\(g(x)=\log_{4}(7x+10)\)
\(h(x)=\log_{3}(3x+7)\)
\(h(x)=\log_{4}(7-8x)\)
\(g(x)=\log_{5}(4-8x)\)
Graph each logarithmic function.
\(f(x)=\log_{4}x\)
\(g(x)=\log_{1/4}x\)
\(q(n)=-\log_{2}n\)
\(h(t)=\log_{1/2}t\)
\(x(t)=-\log t\)
\(w(x)=\ln x\)
Solve each equation.
\(\log_{5}x=1\)
\(\log_{2}x=-2\)
\(\log_{11}k=2\)
\(\log_{9}(n+9)=4\)
\(\log_{5}(-3m)=3\)
\(\log_{11}(x+5)=-1\)
\(\log_{4}(6b+4)=0\)
\(\log_{5}(-10x+4)=4\)
\(\log_{2}(10-5a)=3\)
\(\log_{8}k=3\)
\(\log n=3\)
\(\log_{4}p=4\)
\(\log_{11}(x-4)=-1\)
\(\log_{2}(-8r)=1\)
\(\ln (-3n)=4\)
\(\log_{11}(10v+1)=-1\)
\(\log_{9}(7-6x)=-2\)
\(\log_{8}(3k-1)=1\)