4.2: THE MEAN VALUE THEOREM
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section, we focus on the Mean Value Theorem, one of the most important tools of calculus and one of the most beautiful results of mathematical analysis. The Mean Value Theorem we study in this section was stated by the French mathematician Augustin Louis Cauchy (1789-1857), which follows form a simpler version called Rolle's Theorem.
An important application of differentiation is solving optimization problems. A simple method for identifying local extrema of a function was found by the French mathematician Pierre de Fermat (1601-1665). Fermat's method can also be used to prove Rolle's Theorem.
We start with some basic definitions of minima and maxima. Recall that for
Let
Similarly, we say that
In January 1638, Pierre de Fermat described his method for finding maxima and minima in a letter written to Marin Mersenne (1588-1648) who was considered as "the center of the world of science and mathematics during the first half of the 1600s." His method presented in the theorem below is now known as Fermat's Rule.
Let
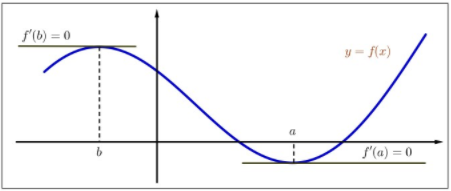
Figure
- Proof
-
Suppose
Since
Taking into account the differentiability of
Similarly,
It follows that
Therefore,
Let
- Proof
-
Since
Then
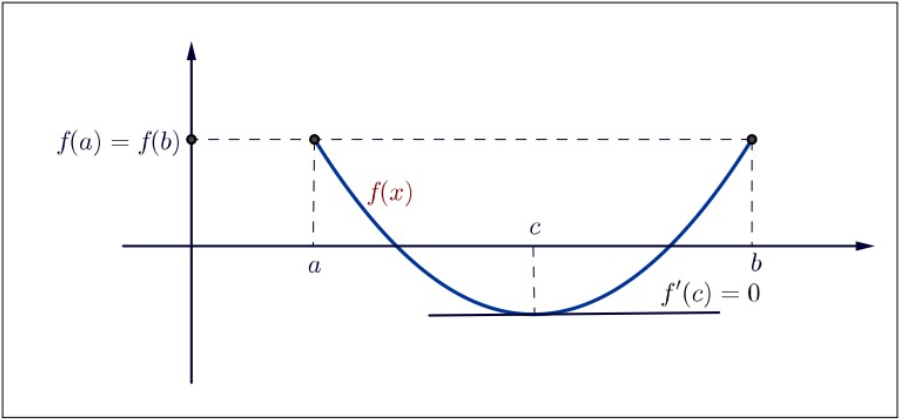
Figure
If
If both
We are now ready to use Rolle's Theorem to prove the Mean Value Theorem presented below.
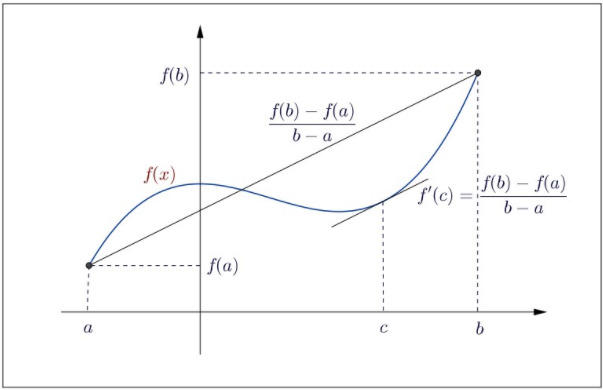
Figure
Let
- Proof
-
The linear function whose graph goes through
Define
Then
it follows that
Thus, (4.5) holds.
We show that
Solution
Let
Therefore,
Then, again,
We show that
Solution
Let
Now, fix
Since
Rearranging terms provides the desired inequality.
A more general result which follows directly from the Mean Value Theorem is known as Cauchy's Theorem.
Let
- Proof
-
Define
Then
this implies (4.6).
The following theorem shows that the derivative of a differentiable function on
Let
exists, we say that
If the limit
exists, we say that
We will say that
Let
Then there exists
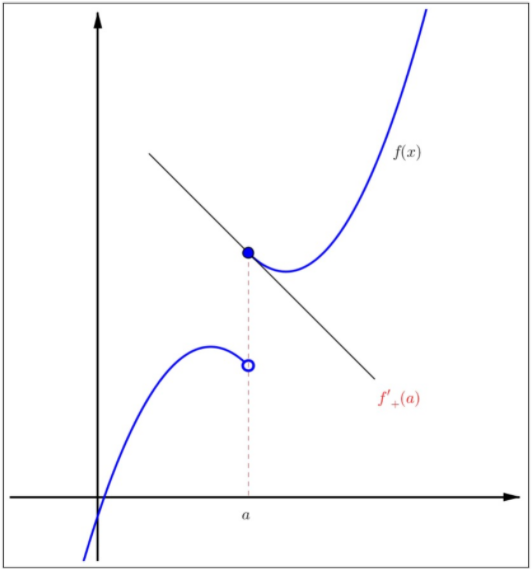
Figure
- Proof
-
Define the function
Then
Thus,
It follows that there exists
SImilarly, there exists
Since
The same conclusion follows if
Exercise
Let
Prove that
- Answer
-
Add texts here. Do not delete this text first.
Exercise
Prove the following inequalities using the Mean Value Theorem.
- Answer
-
Add texts here. Do not delete this text first.
Exercise
Prove that
- Answer
-
Add texts here. Do not delete this text first.
Exercise
Let
has a solution on
- Answer
-
Add texts here. Do not delete this text first.
Exercise
Let
where the bars denote determinants of the two-by-two matrices.
- Answer
-
Add texts here. Do not delete this text first.
Exercise
Let
- Suppose
Prove that the equation
has a solution in
- Suppose
Prove that the equation
has a solution on
- Answer
-
Add texts here. Do not delete this text first.
Exercise
Let
- Answer
-
Add texts here. Do not delete this text first.
Exercise
Let
- Show that if
- Show that if
- Are the converses in part (a) and part (b) true?
- Answer
-
Add texts here. Do not delete this text first.


