Skip to main content
\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
Mathematics LibreTexts

6.9: Discontinuous Forcing

  1. Last updated
  2. Save as PDF
  • Page ID
    388

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    In the last section we looked at the Heaviside function its Laplace transform. Now we will use this tool to solve differential equations.

    Example \(\PageIndex{1}\)

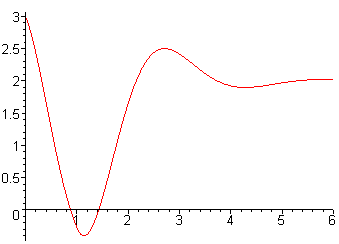
    A 1 kg bar is attached to a spring with spring constant 5 and damping constant 2. It is pulled down 3 inches from it equilibrium position and the released. After one second a constant force of 10 Newtons is exerted on the bar. The force remains turned on indefinitely. Determine the equation of motion of the bar.

    Solution

    We have the differential equation

    \[ y'' + 2y' + 5y = 10u_1(t)\]

    with

    \[ y(0) = 3 \]

    \[ y'(0) = 0 .\]

    We solve this by the method of Laplace transforms. We have

    \[ \begin{align} L\{y''\} + 2L\{y'\} + 5L\{y\} &= 10L\{u_1(t)\} \\ \implies s^2L\{y\} - 3s - 0 + 2(sL\{y\} - 3) + 5L\{y\} &= 10e^{-s} /s \\ \implies (s^2 + 2s + 5)L\{y\} - 3s - 6 &= 10e^{-s} /s \\ \implies L\{y\} &= \dfrac{3s + 6 }{s^2 + 2s + 5} + \dfrac{10 }{s(s^2 + 2s + 5)} . \end{align} \]

    We use partial fractions on the second term

    \[ \dfrac{10}{s(s^2 + 2s + 4)} = \dfrac{A}{s} + \dfrac{Bs+C}{s^2+2s+5} \]

    \[ A(s^2 + 2s + 5) + (Bs + C)s = 10 \]

    \[ (A + B)s^2 + (2A + C)s + 5A = 10 \]

    The constant term gives

    \( A =2 \)

    Thus

    \( B = -2 \) \(C = -4 \)

    We can complete the square

    \[ s^2 + 2s + 5 = (s+1)^2 +4 \]

    Putting all the algebra together we get

    \[ \begin{align*} L\{y\} &= \dfrac{3s + 6}{(s + 1)^2 + 4} + e^{-s}\dfrac{2}{s} + e^{-s}\dfrac{-2s - 4}{ (s + 1)^2 + 4 } \\ &= 3\dfrac{s + 1 + 1}{(s + 1)^2 + 4} + e^{-s}\dfrac{2}{s} - 2e^{-s}\dfrac{(s + 1) + 1 }{(s + 1)^2 + 4 } \\ &= 3\dfrac{s + 1}{(s + 1)^2 + 4} + 3/2 \dfrac{2}{(s + 1)^2 + 4} + e^{-s}\dfrac{2}{s} - 2e^{-s}\dfrac{(s + 1) }{(s + 1)^2 + 4 } - e^{-s}\dfrac{2 }{(s + 1)^2 + 4 } \end{align*}\]

    Now use the table to take the inverse Laplace transform to get

    \[ y = 3e^{-t}\cos(2t) + 3/2 e^{-t -1}\sin(2t) + 2u_1 - 2u_1(t)e^{-t +1}\cos(2t - 2) - u_1(t)e^{-t +1} \sin(2t - 2). \]

    Below is the graph

    Contributors