1.4: Continuous Functions

As \((1.2 .8)\) indicates, we would like to define the rate of change of a function \(y=f(x)\) with respect to \(x\) as the shadow of the ratio of two quantities, \(d y=\) \(f(x+d x)-f(x)\) and \(d x,\) with the latter being a nonzero infinitesimal. From the discussion of the previous section, it follows that we can do this if and only if the numerator \(d y\) is also an infinitesimal.

Definition

We say a function \(f\) is continuous at a real number \(c\) if for every infinitesimal \(\epsilon\),

\[f(c+\epsilon) \simeq f(c)\]

Note that \(f(c+\epsilon) \simeq f(c)\) is equivalent to \(f(c+\epsilon)-f(c) \simeq 0,\) that is, \(f(c+\epsilon)-f(c)\) is an infinitesimal. In other words, a function \(f\) is continuous at a real number \(c\) if an infinitesimal change in the value of \(c\) results in an infinitesimal change in the value of \(f\).

Example \(\PageIndex{1}\)

If \(f(x)=x^{2},\) then, for example, for any infinitesimal \(\epsilon\),

\[f(3+\epsilon)=(3+\epsilon)^{2}=9+6 \epsilon+\epsilon^{2} \simeq 9=f(3) .\]

Hence \(f\) is continuous at \(x=3 .\) More generally, for any real number \(x\),

\[f(x+\epsilon)=(x+\epsilon)^{2}=x^{2}+2 x \epsilon+\epsilon^{2} \simeq x^{2}=f(x) ,\]

from which it follows that \(f\) is continuous at every real number \(x .\)

Exercise \(\PageIndex{1}\)

Verify that \(f(x)=3 x+4\) is continuous at \(x=5\).

Exercise \(\PageIndex{2}\)

Verify that \(g(t)=t^{3}\) is continuous at \(t=2\).

Solution

Given real numbers \(a\) and \(b,\) we let

\[(a, b)=\{x | x \text { is a real number and } a<x<b\} ,\]

\[(a, \infty)=\{x | x \text { is a real number and } x>a\} ,\]

\[(-\infty, b)=\{x | x \text { is a real number and } x<b\} ,\]

and

\[(-\infty, \infty)=\mathbb{R} .\]

An open interval is any set of one of these forms.

Definition

We say a function \(f\) is continuous on an open interval \(I\) if \(f\) is continuous at every real number in \(I\).

Example \(\PageIndex{2}\)

From our example above, it follows that \(f(x)=x^{2}\) is continuous on \((-\infty, \infty)\).

Exercise \(\PageIndex{3}\)

Verify that \(f(x)=3 x+4\) is continuous on \((-\infty, \infty)\).

Exercise \(\PageIndex{4}\)

Verify that \(g(t)=t^{3}\) is continuous on \((-\infty, \infty)\).

Exercise \(\PageIndex{3}\)

We call the function

\[ H(t)=\left\{\begin{array}{ll}{0,} & {\text { if } t<0,} \\ {1,} & {\text { if } t \geq 0,}\end{array}\right. \] the Heaviside function (see Figure 1.4.1). If \(\epsilon\) is a positive infinitesimal, then \[ H(0+\epsilon)=H(\epsilon)=1=H(0) , \] whereas \[ H(0-\epsilon)=H(-\epsilon)=0 . \] Since 0 is not infinitesimally close to \(1,\) it follows that \(H\) is not continuous at \(0 .\) However, for any positive real number \(a\) and any infinitesimal \(\epsilon\) (positive or negative), \[ H(a+\epsilon)=1=H(a) , \] since \(a+\epsilon>0,\) and for any negative real number \(a\) and any infinitesimal \(\epsilon\), \[ H(a+\epsilon)=0=H(a) , \] since \(a+\epsilon<0 .\) Thus \(H\) is continuous on both \((0, \infty)\) and \((-\infty, 0)\).

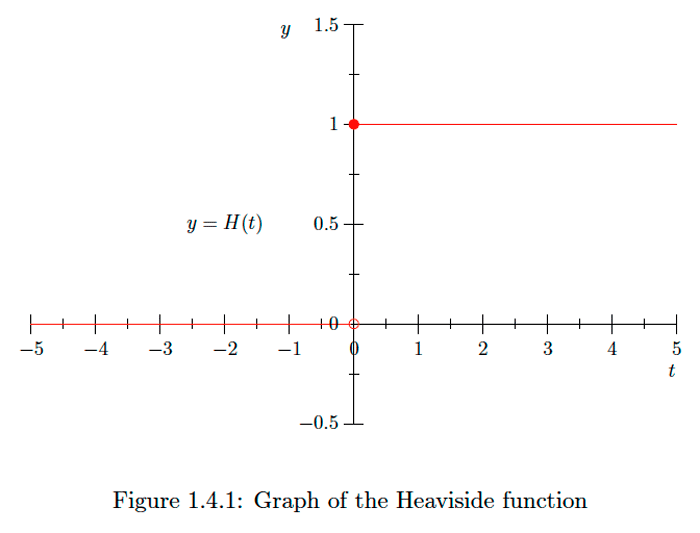
Note that, in the previous example, the Heaviside function satisfies the condition for continuity at 0 for positive infinitesimals but not for negative infinitesimals. The following definition addresses this situation.

Definition

We say a function \(f\) is continuous from the right at a real number \(c\) if for every infinitesimal \(\epsilon>0\),

\[ f(c+\epsilon) \simeq f(c) . \] Similarly, we say a function \(f\) is continuous from the left at a real number \(c\) if for every infinitesimal \(\epsilon>0\), \[ f(c-\epsilon) \simeq f(c) . \]

Example \(\PageIndex{4}\)

In the previous example, \(H\) is continuous from the right at \(t=0,\) but not from the left.

Of course, if \(f\) is continuous both from the left and the right at \(c,\) then \(f\) is continuous at \(c .\)

Example \(\PageIndex{5}\)

Suppose

\[ f(x)=\left\{\begin{array}{ll}{3 x+5,} & {\text { if } x \leq 1,} \\ {10-2 x,} & {\text { if } x>1.}\end{array}\right. \] If \(\epsilon\) is a positive infinitesimal, then \[ f(1+\epsilon)=3(1+\epsilon)+5=8+3 \epsilon \simeq 8=f(1) , \] so \(f\) is continuous from the right at \(x=1,\) and \[ f(1-\epsilon)=3(1-\epsilon)+5=8-3 \epsilon \simeq 8=f(1) , \] so \(f\) is continuous from the left at \(x=1\) as well. Hence \(f\) is continuous at \(x=1\).

Exercise \(\PageIndex{5}\)

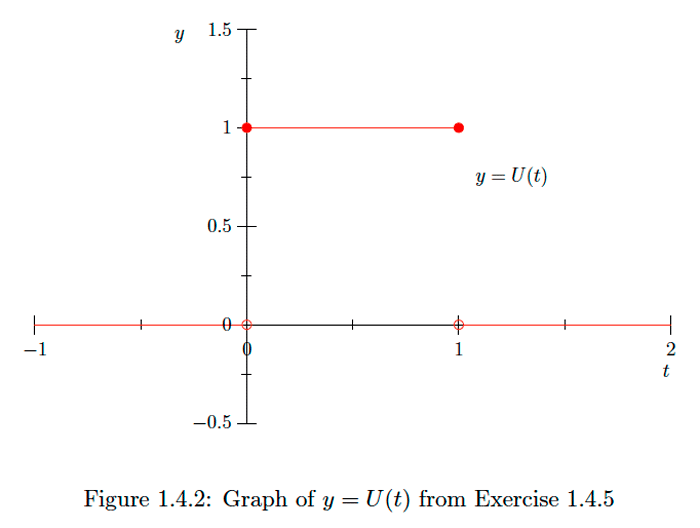
Verify that the function

\[ U(t)=\left\{\begin{array}{ll}{0,} & {\text { if } t<0,} \\ {1,} & {\text { if } 0 \leq t \leq 1,} \\ {0,} & {\text { if } t>1,}\end{array}\right. \] is continuous from the right at \(t=0\) and continuous from the left at \(t=1,\) but not continuous at either \(t=0\) or \(t=1 .\) See Figure \(1.4 .2 .\) Given real numbers \(a\) and \(b,\) we let \[ [a, b]=\{x | x \text { is a real number and } a \leq x \leq b\} , \] \[ [a, \infty)=\{x | x \text { is a real number and } x \geq a\} , \] and \[ (-\infty, b]=\{x | x \text { is a real number and } x \leq b\} . \] A closed interval is any set of one of these forms.

Definition

If \(a\) and \(b\) are real numbers, we say a function \(f\) is continuous on the closed interval \([a, b]\) if \(f\) is continuous on the open interval \((a, b),\) continuous from the right at \(a\), and continuous from the left at \(b\). We say \(f\) is continuous on the closed interval \([a, \infty)\) if \(f\) is continuous on the open interval \((a, \infty)\) and continuous from the right at \(a .\) We say \(f\) is continuous on the closed interval \((-\infty, b]\) if \(f\) is continuous on \((-\infty, b)\) and continuous from the left at \(b\).

Example \(\PageIndex{6}\)

We may summarize our results about the Heaviside function as \(H\) is continuous on \((-\infty, 0)\) and on \([0, \infty)\).

Exercise \(\PageIndex{6}\)

Explain why the function \(U\) in the previous exercise is continuous on the intervals \((-\infty, 0),[0,1],\) and \((1, \infty),\) but not on the interval \((-\infty, \infty) .\)