9.1: Compound Interest Fundamentals
( \newcommand{\kernel}{\mathrm{null}\,}\)
Five years ago you started a long-term GIC. The bank statement shows that you originally placed $15,000 into the account earning 5.95% in annually compounded interest. You now have $20,026.09. In the first year of the GIC, you earned $892.50 in interest. Subsequent years earned annual interest amounts of $945.60, $1,001.87, $1,061.48, and finally $1,124.64. Of course, you like that the interest amount increased each year even though you did not make any more deposits to the GIC, but why did this happen?
The Concept of Compounding
Simple interest, compound interest—what is the big difference? As you can see in the figure below, simple and compound interest calculations share the same fundamentals of time, interest rate, and placing interest into the account. But the accumulation is not the same, and over time the growth of compound interest will far outpace that of simple interest.
In both forms of interest, the principal is the starting amount that accumulates interest for a length of time at a specified interest rate. But you calculate simple interest in direct proportion to the starting amount, the interest rate, and the time period, whereas the calculation for compound interest is, well, not so simple!
The critical difference is the placement of interest into the account. Under simple interest, you convert the interest to principal at the end of the transaction's time frame. For example, in a six-month simple interest GIC the balance in its account at any point before the maturity date is the original principal and nothing more. Only upon maturity does the interest appear. In contrast, a five-year compound interest GIC such as the one discussed in the section opener receives an interest deposit annually. After one year the principal increases from $15,000 to $15,892.50. This higher principal in the second year explains why the interest earned in the second year then increases as well.
Invest $1,000 for 25 years at both 10% simple interest and 10% interest compounded annually. As demonstrated in the figure and table below, $1,000 invested at 10% per year of simple interest has a $3,500 balance after 25 years. This consists of the original $1,000 principal plus $2,500 in total interest ($100 for each year the money was invested). However, $1,000 invested at 10% compounded annually has a balance of $10,834.71, which is $7,334.71 more! This difference is the result of interest being converted to principal and thus earning even more interest for you. A close examination of the first two years reveals the following:
- In the first year, both investments have a $1,100 balance. With simple interest, the $100 of interest remains as accrued interest and is not placed into the account while the principal remains at $1,000. With compound interest, the $100 of interest is converted to principal, resulting in a $1,100 principal for the second year.
- In the second year, the simple interest account still has a $1,000 principal, which earns another $100 of interest ($1,000 × 10% = $100). The account now has $1,000 of principal plus $200 in accrued interest. The compound interest account earns 10% on the new principal of $1,100, or $110 of interest ($1,100×10%=$110). This interest is placed into the account at the end of year two, making the principal $1,210 for the third year . . . and so on.
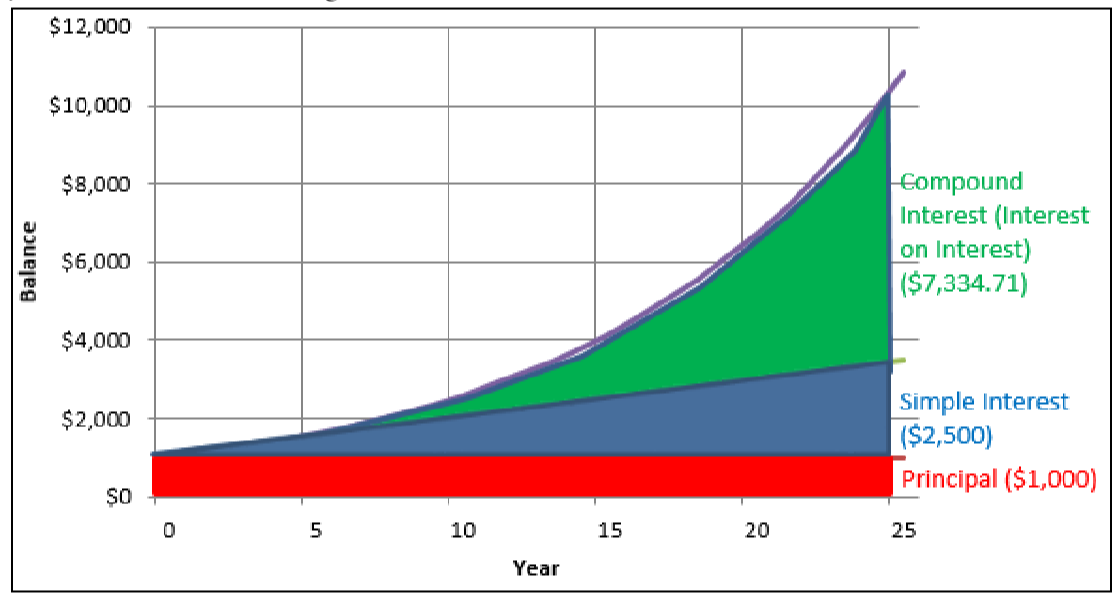
Figure 9.1.1
| At 10% Simple Interest | At 10% Compound Interest | |||||
|---|---|---|---|---|---|---|
| End of Year | Principal | Accrued Interest | Balance | Principal | Accrued Interest | Balance |
| Start | $1,000.00 | |||||
| 1 | $1,000.00 | $100.00 | $1,100.00 | $1,000.00 | $100.00 | $1,100.00 |
| 2 | $1,000.00 | $200.00 | $1,200.00 | $1,100.00 | $110.00 | $1,210.00 |
| 3 | $1,000.00 | $300.00 | $1,300.00 | $1,210.00 | $121.00 | $1,331.00 |
| 4 | $1,000.00 | $400.00 | $1,400.00 | $1,331.00 | $133.10 | $1,464.10 |
| 5 | $1,000.00 | $500.00 | $1,500.00 | $1,464.10 | $146.41 | $1,610.51 |
| ..... | ..... | ..... | ..... | ..... | ..... | |
| 10 | $1,000.00 | $1,000.00 | $2,000.00 | $2,357.95 | $235.79 | $2,593.74 |
| ..... | ..... | ..... | ..... | ..... | ..... | |
| 15 | $1,000.00 | $1500.00 | $2,500.00 | $3,797.50 | $379.75 | $4,177.25 |
| ..... | ..... | ..... | ..... | ..... | ..... | |
| 20 | $1,000.00 | $2000.00 | $3,000.00 | $6,115.91 | $611.59 | $6,727.50 |
| ..... | ..... | ..... | ..... | ..... | ..... | |
| 25 | $1,000.00 | $2500.00 | $3,500.00 | $9.849.73 | $984.98 | $10,834.71 |
Ultimately, as the principal in the compound interest account increases, the amount of interest earned also increases. Observe that the difference in the balance between simple interest and compound interest in the first five years is slight, but the gap widens over time.
Compound Interest Rates
If an equal amount of principal invested for 25 years earns an interest rate of 9% compounded annually versus 3% compounded annually, would the interest accumulated by the 9% investment be three times as large?
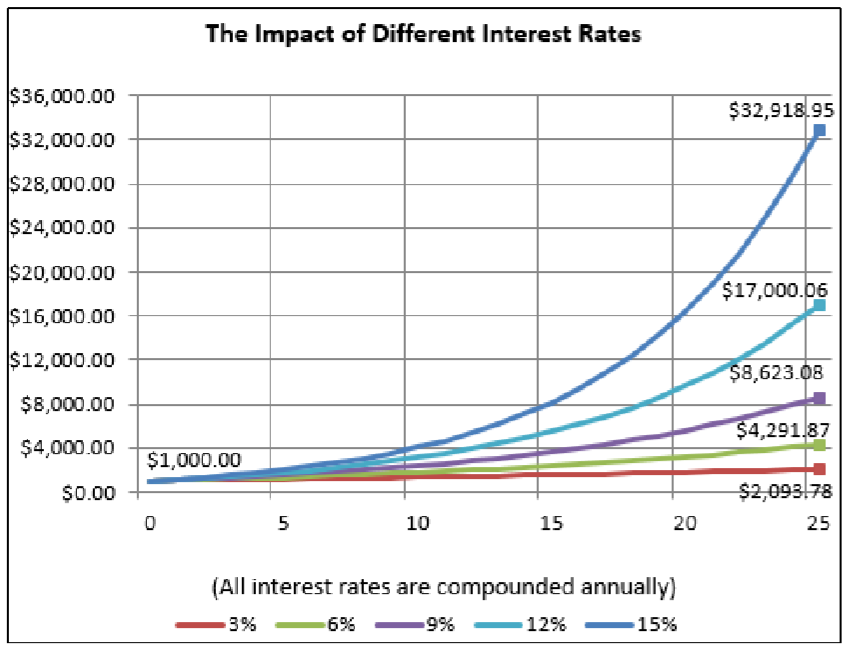
Figure 9.1.2
In a simple interest environment, this would be true since the principal never changes: in each of the 25 years the amounts of simple interest would be constant, and the amount for the 9% investment would be three times larger than for the 3% investment. However, in compound interest each subsequent year’s interest is compounded on an increasingly larger principal. This chart shows $1,000 invested at five different annually compounded rates. Observe the following after 25 years:
- The investment at 9% compounded annually has a balance of $8,623.08 compared to $2,093.78 for the 3% compounded annually. Therefore, the interest earned is $7,623.08 versus $1,093.78, reflecting a ratio approximating 7 : 1.
- Comparing the 15% interest rate versus the 6% interest rate, many people imagine the final balances would be in the same ratio as the ratio of the rates, 15% : 6%, which simplifies to 2½ : 1. However, in the chart, the final balances are $32,918.95 versus $4,291.87, reflecting a ratio approximating 7⅔ : 1!
These examples illustrate that in compound interest scenarios, the ratio of interest earned is not directly proportionate to the numerical ratio of the interest rates. Higher interest rates result in higher interest amounts, therefore yielding more principal upon which future interest is earned. Over a long time period, this growth in the balance is exponential.
How Often Interest Compounds
The examples so far have involved compound interest that has been compounded annually—the accrued interest is being converted to principal at the end of every year. But this is not the only option. Interest can be converted to principal at any frequency, including daily, weekly, monthly, quarterly (every three months), or semi-annually (every six months). Under any of these options the principal increases more frequently, which in turn results in more interest being earned.
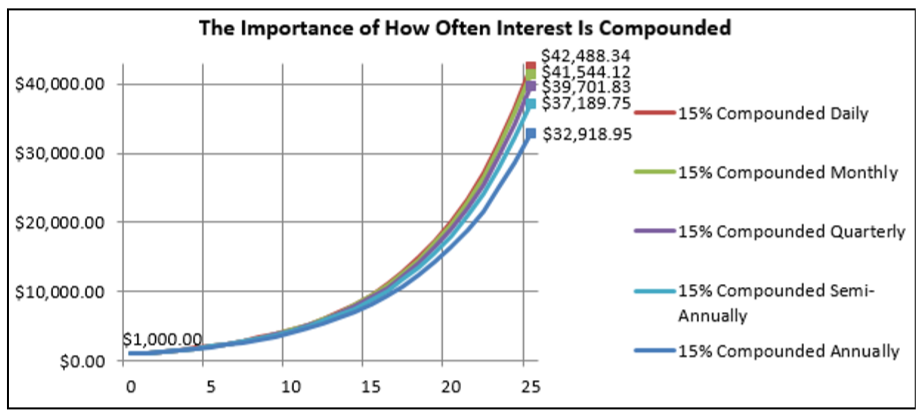
Figure 9.1.3
The chart in the figure above illustrates the impact of different compounding frequencies. In the case of monthly versus annual compounding, the monthly compound increases the account balance every month whereas the annual compound increases the balance once every 12 months. To understand why the monthly compound earns more interest, note that after each month the principal increases and therefore earns more interest. Each of the 12 increases is small on its own, but the cumulative effect is large: by having the interest deposited every month instead of every year, over the course of 25 years an additional $41,544.12−$32,918.95=$8,625.17 in interest is earned!
Paths To Success
The table below summarizes the desirable characteristics when either investing or borrowing.
| Investing | Characteristic | Borrowing |
|---|---|---|
| Compound | Type of Interest | Simple |
| You want your interest to earn you more interest. | You don't want interest being converted to principal. | |
|
⇑ The higher the rate, the more you earn. |
Interest Rate |
⇓ The lower the rate, the less you pay. |
|
⇑ The more often it compounds, the more principal that can earn interest. A daily compound would be best! |
Compounding |
⇓ The less often it compounds, the less principal that can earn interest. An annual compound would be best! |
|
⇑ As the principal continually grows, you earn more interest. Longer time frames are desirable. |
Time (or Term) |
⇓ You don't want the principal to grow and earn more interest. Short time frames are desirable. |
Calculating the Periodic Interest Rate
The first step in learning about investing or borrowing under compound interest is to understand the interest rate used in converting interest to principal. You commonly need to convert the posted interest rate to find the exact rate of interest earned or charged in any given time period.
The Formula
Formula 9.1 involves four key concepts, which are explained next, to do with conversion of the interest rate.

How It Works
To solve any question involving the periodic interest rate, follow these steps:
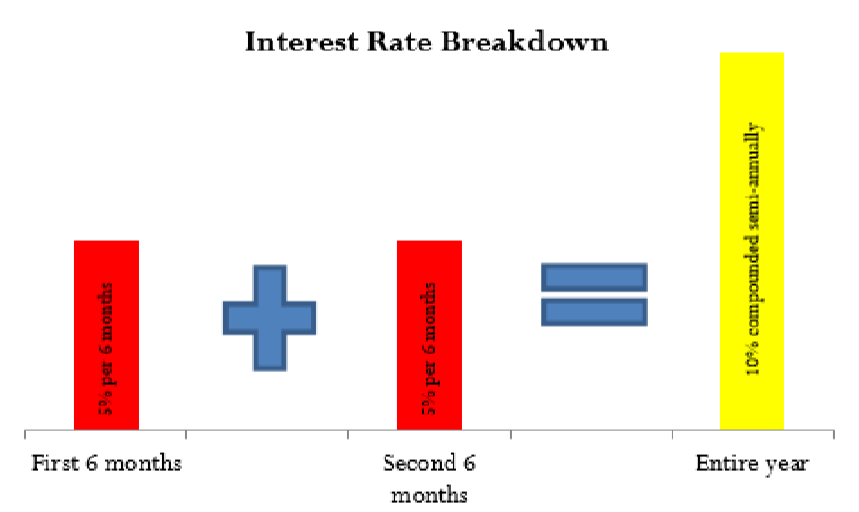
Figure 9.1.4
Step 1: Identify two of the three key variables—the nominal interest rate (IY), compounding frequency (CY), or periodic interest rate (i).
Step 2: Substitute into Formula 9.1, rearranging if needed, and solve for the unknown variable. If you calculate the compound frequency (CY), you must convert the number back into the compounding words associated with the frequency. For example, CY = 2 means twice per year and is stated as “semi-annually.”
An example involving the calculation of the periodic interest rate for “10% compounded semi-annually” illustrates these steps.
Step 1: The wording “semi-annually” means the compounding period is every six months. One year contains two such compounding periods, making the compounding frequency twice per year, or CY = 2. The nominal annual interest rate is 10%, or IY = 10%.
Step 2: Applying Formula 9.1, calculate the periodic interest rate as i=10%÷2=5%. Figure 9.1.4 illustrates that every six months 5% interest is converted to principal. You could look at the nominal interest rate for the year, 10%, as the total of the periodic interest rates for each of the two periods. But remember, unlike with simple interest, the actual interest amount here will increase from one period to the next.
Important Notes
When you express a compound interest rate, you must always state the words for the compounding frequency along with the nominal annual number. For example, you must say “10% compounded semi-annually” and not just "10%." In the absence of an explicit compounding frequency, the number is interpreted by default to mean “compounded annually” except if an industry standard dictates otherwise. For example, in the case of mortgages in Canada, the default is semi-annual compounding, so when you hear of a 10% mortgage, you should assume it to be 10% compounded semi-annually. But in most industries “10%” with no words generally means “10% compounded annually.”
Things To Watch Out For
It is common to confuse the compounding period and the compounding frequency. The table below shows the relationship between compounding periods and frequencies. Remember that to calculate the periodic interest rate you need the compounding frequency, not the compounding period.
| Common Compounds | Compounding Period | Compounding Frequency (CY) |
|---|---|---|
| Annually | Every year | 1 |
| Semi-annually | Every 6 months | 2 |
| Quarterly | Every 3 months | 4 |
| Monthly | Every 1 month | 12 |
| Weekly | Every 1 week | 52* |
| Daily | Every day | 365* |
*Note that although there are not exactly 52 weeks in a year and there are 366 days in a leap year, it is common practice to use these values for compounding frequency.
Paths To Success
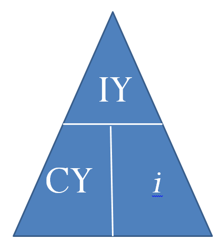
For ease of manipulation, you can remember the rearrangement of Formula 9.1 using the triangle technique once again. Recall that as long as you know any two pieces of the puzzle, you can solve for the third.
- If you are investing money, what interest characteristics should you seek out?
- If you are borrowing money, what interest characteristics should you seek out?
- Of 10% compounded semi-annually or 10% compounded monthly, which earns more interest?
- If you invested a principal at the same compounded interest rate for 20 years, would the amount of interest earned in the second 10 years be less than twice, exactly twice, or more than twice the interest earned during the first 10 years?
- John has an interest rate of 4% compounded annually while Dwayne is earning 8% compounded annually. If both people placed the same principal into their investments for 25 years, would Dwayne have twice, less than twice, or more than twice as much money as John?
- Of 10% simple interest or 10% interest compounded annually, which earns more interest over time?
- Of the periodic interest rate or the nominal interest rate, which is always at least as large as the other?
- Answer
-
- High interest rate, high compounding frequency, long time frames, compound interest.
- Low interest rate, low compounding frequency, short time frames, simple interest.
- 10% monthly, as demonstrated in Figure 9.1.3.
- More than twice, as demonstrated in Figure 9.1.2.
- More than twice, as demonstrated in Figure 9.1.2.
- 10% compounded annually, as demonstrated in Figure 9.1.1.
- The nominal interest rate.
Calculate the periodic interest rate for the following nominal interest rates:
- 9% compounded monthly
- 6% compounded quarterly
Solution
For each question, calculate the periodic interest rate (i).
What You Already Know
Step 1:
For each question, use the following nominal interest rate and compounding frequency:
- IY = 9%; CY = monthly = 12 times per year
- IY = 6%; CY = quarterly = 4 times per year
How You Will Get There
Step 2:
For each question apply Formula 9.1.
Perform
- i=9%12=0.75% per month
- i=6%4=1.5% per quarter
Present
- Nine percent compounded monthly is equal to a periodic interest rate of 0.75% per month. This means that interest is converted to principal 12 times throughout the year at the rate of 0.75% each time.
- Six percent compounded quarterly is equal to a periodic interest rate of 1.5% per quarter. This means that interest is converted to principal 4 times (every three months) throughout the year at the rate of 1.5% each time.
Calculate the nominal interest rate for the following periodic interest rates:
- 0.58¯3% per month
- 0.05% per day
Solution
For each question, calculate the nominal interest rate (IY).
What You Already Know
Step 1:
For each question, use the following periodic interest rate and compounding frequency:
- i=0.58¯3%; CY = monthly = 12 times per year
- i=0.05%; CY = daily = 365 times per year
How You Will Get There
Step 2:
For each question, apply Formula 9.1 and rearrange for IY.
Perform
- 0.58¯3%=1Y12; IY=0.58¯3%×12=7% compounded monthly
- 0.05%=IY365; IY=0.05%×365=18.25% compounded daily
Present
- A periodic interest rate of 0.58¯3% per month is equal to a nominal interest rate of 7% compounded monthly.
- A periodic interest rate of 0.05% per day is equal to a nominal interest rate of 18.25% compounded daily.
Calculate the compounding frequency for the following nominal and periodic interest rates:
- nominal interest rate = 6%, periodic interest rate = 3%
- nominal interest rate = 9%, periodic interest rate = 2.25%
Solution
For each question, calculate the compounding frequency (CY) and convert the calculated number to words.
What You Already Know
Step 1:
For each question, use the following nominal and periodic interest rates:
- IY = 6%; i = 3%
- IY = 9%; i = 2.25%
How You Will Get There
Step 2:
For each question, apply Formula 9.1 and rearrange for CY.
Perform
- 3%=6%CY; CY=6%3%=2 compounds per year = semi-annually
- 2.25%=9%CY; CY=9%2.25%=4 compounds per year = quarterly
Present
- For the nominal interest rate of 6% to be equal to a periodic interest rate of 3%, the compounding frequency must be twice per year, which means a compounding period of every six months, or semi-annually.
- For the nominal interest rate of 9% to be equal to a periodic interest rate of 2.25%, the compounding frequency must be four times per year, which means a compounded period of every three months, or quarterly.


