9.2: Determining the Future Value
- Page ID
- 22118
Your company has an employee assistance plan through which employees can borrow funds at 12% compounded semi-annually, much like a loan from a bank, then repay the money at their convenience. An employee who borrowed $4,000 two years ago has been unable to repay the loan until today. As the human resources manager in charge of the assistance plan, you must tell him the exact amount he needs to pay to return his balance to zero. How do you do this?
Now that you know how to calculate the periodic interest rate, you can compute compound interest. This chapter focuses on single amounts, also called lump-sum amounts. This knowledge will form the basis for you to work with compound interest on a series of payments, which will be covered in Chapter 11 through Chapter 15. Investing the time now to understand these fundamentals will reap dividends as you proceed in your studies of business mathematics.
Future Value Calculations with No Variable Changes
The simplest future value scenario for compound interest is for all of the variables to remain unchanged throughout the entire transaction. To understand the derivation of the formula, continue with the opening scenario. If the money was borrowed two years ago, then the employee will owe two years of compound interest in addition to the original principal of $4,000. That means \(PV\) = $4,000. The compounding frequency is semi-annually, or twice per year, which makes the periodic interest rate \(i=\dfrac{12 \%}{2}=6 \%\). Therefore, after the first six months, your employee has 6% interest converted to principal. This a future value, or \(FV\), calculated as follows:
Principal after one compounding period (six months) = Principal plus interest
\[\begin{aligned}
FV &=PV+{i}(PV) \\
&=\$ 4,000+0.06(\$ 4,000) \\
&=\$ 4,000+\$ 240=\$ 4,240
\end{aligned}\nonumber \]
Now proceed to the next six months. The future value after two compounding periods (one year) is calculated in the same way. Note that the equation \(FV=PV+i(PV)\) can be factored and rewritten as \(FV=PV(1+i)\).
\(FV\) (after two compounding periods) = \(PV(1+i)=\$4,240(1+0.06)=\$ 4,240(1.06)=\$ 4,494.40\)
Since the \(PV=\$ 4,240\) is a result of the previous calculation where \(PV(1+i)=\$ 4,240\), the following algebraic substitution is possible:
\[FV=PV(1+i)(1+i)=\$ 4,000(1.06)(1.06)=\$ 4,240(1.06)=\$ 4,494.40\nonumber \]
Applying exponent rules from Section 2.4 and simplifying it algebraically, you get:
\[FV=PV\left(1+i\right)\left(1+i\right)=PV\left(1+i\right)^{2}\nonumber \]
Do you notice a pattern? With one compounding period, the formula has only one \((1 + i)\). With two compounding periods involved, it has two factors of \((1 + i)\). Each successive compounding period multiplies a further \((1 + i)\) onto the equation. This makes the exponent on the \((1 + i)\) exactly equal to the number of times that interest is converted to principal during the transaction.
The Formula
First, you need to know how many times interest is converted to principal throughout the transaction. You can then calculate the future value. Use Formula 9.2 to determine the number of compound periods involved in the transaction

Once you know \(N\), substitute it into Formula 9.3, which finds the amount of principal and interest together at the end of the transaction, or the maturity value.
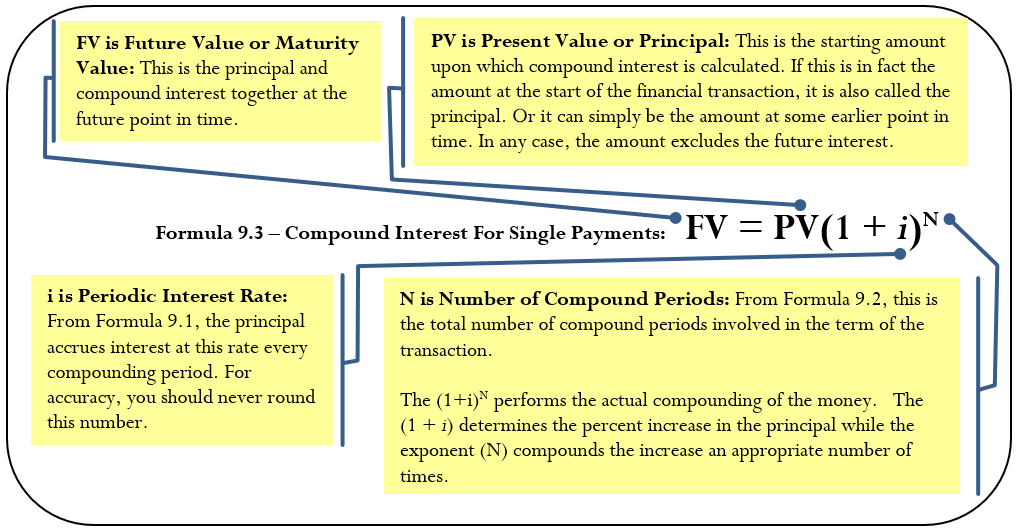
How It Works
Follow these steps to calculate the future value of a single payment:
Step 1: Read and understand the problem. If necessary, draw a timeline similar to the one here identifying the present value, the nominal interest rate, the compounding, and the term.

Step 2: Calculate the periodic interest rate (\(i\)) from Formula 9.1.
Step 3: Calculate the total number of compound periods (\(N\)) from Formula 9.2.
Step 4: Solve Formula 9.3. Revisit the employee who had $4,000 outstanding for two years with interest at 12% compounded semi-annually.

Step 1: Calculate the amount of the loan after two years (\(FV\)). Observe that \(PV\) = $4,000, \(IY\) = 12%, \(CY\) = 2 (every six months or twice per year), and Years = 2.
Step 2: According to Formula 9.1, \(i=\dfrac{12 \%}{2}=6 \%\). Thus, interest at a rate of 6% is converted to principal at the end of each compounding period of six months.
Step 3: Applying Formula 9.2, \(N=CY \times \text { Years }=2 \times 2=4\). Interest is converted to principal four times over the course of the two-year term occurring at the 6, 12, 18, and 24 month marks.
Step 4: Calculate the maturity value using Formula 9.3: \[FV=\$ 4,000(1+0.06)^{4}=\$ 5,049.91 \nonumber \]
To pay off the loan the employee owes $5,049.91.
Important Notes
Calculating the Interest Amount:
In any situation of lump-sum compound interest, you can isolate the interest amount using an adapted Formula 8.3:
\[I=S-P \text { becomes } I=FV-PV\nonumber \]
Using your employee's $4,000 loan with a future repayment of $5,049.91, the interest paid is calculated as
\[I=\$ 5,049.91-\$ 4,000.00=\$ 1,049.91\nonumber \]
This formula applies only to compound interest situations involving lump-sum amounts. If regular payments are involved, this is called an annuity, for which a modified version of the interest formula will be introduced in Chapter 11.
The BAII Plus Calculator:
Your BAII Plus calculator is a business calculator pre-programmed with compound interest formulas. These functions are called the “time value of money” buttons. The compound interest buttons are found in two areas of the calculator, as shown in the photo.

- The five buttons located on the third row of the calculator are five of the seven variables required for time value of money calculations. This row’s buttons are different in color from the rest of the buttons on the keypad. The table on the next page relates each button to formula symbols used in this text along with what each button represents and any data entry requirements.To enter any information into any one of these buttons, key in the data first and then press the appropriate button. For example, if you want to enter \(N\) = 34, then key in 34 followed by pressing \(N\).
| Calculator Symbol | Formula Symbol | Characteristic | Data Entry Requirements |
|---|---|---|---|
| N | \(N\) | The number of compounding periods (from Formula 9.2) | An integer or decimal number; no negatives |
| I/Y | \(IY\) | The nominal interest rate per year | Percent format without the % sign (i.e., 7% is just 7) |
| PV | \(PV\) | Present value or principal | An integer or decimal number |
| PMT | \(PMT\) | Used for annuity payment amounts (covered in Chapter 11) and is not applicable to lump-sum amounts; it needs to be set to zero for lump-sum calculations | An integer or decimal number |
| FV | \(FV\) | Future value or maturity value | An integer or decimal number |
- Since frequency and interest rates are related, as shown in Formula 9.1, the frequency function is logically placed above the I/Y button and it is labelled P/Y. This function addresses compound interest frequencies, such as the compounding frequency. Access the function by pressing 2nd P/Y to find the entry fields shown in the table below, which you can scroll through using the i and h arrow buttons. To exit the P/Y window, press 2nd Quit.
| Calculator Symbol | Formula Symbol | Characteristic | Data Entry Requirements |
|---|---|---|---|
| P/Y | \(PY\) | Annuity payments per year (payment frequency is introduced in Chapter 11); when working with lump-sum payments and not annuities, the calculator requires this variable to be set to match the C/Y | A positive, nonzero number only |
| C/Y | \(CY\) | Compounds per year (compounding frequency) | A positive, nonzero number only |
The table relates each window variable to the formula symbols along with what each button represents and its data entry requirements. To enter information into these variables, key in the data first and then press Enter. For example, to enter a compounding frequency of 4, press 4 while C/Y is on your screen and then press Enter. Most commonly the P/Y and C/Y are the same number, as demonstrated in later chapters. Therefore, the calculator’s built-in shortcut feature automatically copies any value entered into the P/Y variable to the C/Y variable. If the P/Y and C/Y are not the same, you can scroll down and re-enter the C/Y as needed.
BAII Plus Cash Flow Sign Convention:
An investment and a loan are very different. An investment earns interest and the principal increases over time. A loan is charged interest but is usually paid off through payments, resulting in the principal decreasing over time. Notice that nowhere on the calculator is there a button to enter this critical piece of information. How does the calculator distinguish between the two? You must apply a principle called the cash flow sign convention to the \(PV\), \(PMT\), and \(FV\) buttons:

- If you have money leaving your possession and going somewhere else (such as being put into an investment or making a payment against a loan), you must enter the number as a NEGATIVE number.
- If you have money coming into your possession and you are receiving it (such as borrowing money from the bank or having an investment mature and pay out to you), you must enter the number as a POSITIVE number.
When doing financial calculations it is important to “be somebody” in the transaction. In any compound interest scenario, two parties are always involved—somebody is investing and somebody is borrowing. From this standpoint, think about whether the money leaves you or comes at you. This will help you place the correct sign in front of the \(PV\), \(PMT\), and \(FV\) when using your calculator. Who you are will not change the numbers of the transaction, just the cash flow sign convention.
- If you borrow money from your friend and then pay it back, the initial loan is received by you and hence entered as a positive \(PV\) for you. As you pay back the loan, money leaves you and therefore the \(FV\) is negative for you.
- Taking the other side of the coin and being your friend, the loaning of money is a negative \(PV\) for him. When you repay the loan, your friend receives it and therefore results in a positive \(FV\) for him.
Notice that the \(PV\) and \(FV\) always have opposite signs. Investments must always mature, providing a payback to the investor. Loans must always be repaid.
BAII Plus Memory:
Your calculator has permanent memory. Once you enter data into any of the time value buttons it is permanently stored until
- You override it by entering another piece of data and pressing the button;
- You clear the memory of the time value buttons by pressing 2nd CLR TVM before proceeding with another question; or
- The reset button on the back of the calculator is pressed.
This permanent storage is an advantage in multistep compound interest problems. If any piece of information remains constant from step to step, you need to enter it only once.
BAII Plus Keying in a Question:
Seven variables are involved with compound interest. To solve any compound interest question, you must key in six of them. To solve for the missing variable, press CPT followed by the variable. For example, if solving for future value, press CPT FV.
Returning to the employee loan example where a $4,000 loan was taken for two years at 12% interest compounded semi-annually, recall that \(N\) = 4, \(I/Y\) = 12, \(PV\) = $4,000, and \(CY\) = 2. Assuming the role of the employee, you would key in the problem in the following sequence:
- 2nd CLR TVM (clear the memory; this is not required, but it reduces the chance of using stale data)
- 4 \(N\) (total number of compounding periods)
- 12 \(I/Y\) (the nominal interest rate)
- 4000 \(PV\) (a positive since the employee received the money from the company)
- 0 \(PMT\) (you will not use this button until you get to annuities in Chapter 11)
- 2nd \(P/Y\) (to open the frequency window)
- 2 Enter (the \(P/Y\) and \(C/Y\) are the same when working with lump-sum amounts; by entering the \(C/Y\) here, you simultaneously set both variables to the same number)
- 2nd Quit (to close the window)
- CPT \(FV\)
Answer: -5,049.91 (it is negative since the employee owes this money)
Things To Watch Out For
The most common error in the application of Formula 9.3 is to substitute the nominal interest rate for the periodic interest rate. Hence, for 12% compounded semi-annually you might inadvertently use a mistaken value of \(i\) = 0.12 instead of the appropriate \(i\) = 0.06. Formula 9.3 encompasses Formula 9.1 and Formula 9.2. If you write Formula 9.3 without requiring any substitution it appears as follows:
\[FV=PV\left(1+\dfrac{IY}{CY}\right)^{(CY \times \text {Years})} \nonumber \]
Although you could use this equation instead of the one presented in Formula 9.3, most students find it best to use the sequence of three formulas. This requires the systematic approach involved in steps 2 to 4 of the process:
- Calculate \(i\).
- Calculate \(N\).
- Calculate \(FV\).
Use the phrase “iN the Future” to remember this process.
Paths To Success
When you compute solutions on the BAII Plus calculator, one of the most common error messages displayed is "Error 5." This error indicates that the cash flow sign convention has been used in a manner that is financially impossible. Some examples of these financial impossibilities include loans with no repayment or investments that never pay out. In these cases, the PV and FV have been incorrectly set to the same cash flow sign.
-
Formula 9.3, \(FV=PV(1+i)^{N}\), places the number of compound periods into the exponent.
- Answer
-
- The 8% compounded monthly investment realizes 60 compound periods of interest over the five years, while the 8% compounded annually investment realizes only five compound periods. With interest going in much more often, the principal is increasingly larger and therefore earns more interest.
- Each compound period increases the existing principal by the periodic rate through multiplication. Since the periodic interest rate in each compound period multiplies onto the existing principal amount, you apply exponent rules for adding exponents with the same base. The total number of increases in principal equals the number of compound periods in the transaction. See pages xxx–xxx for a full explanation.
If you invested $5,000 for 10 years at 9% compounded quarterly, how much money would you have?
Solution
Calculate the principal and the interest together, which is called the maturity value (\(FV\)).
What You Already Know
Step 1:
The principal, interest rate, and term, as illustrated in the timeline, are known.

How You Will Get There
Step 2:
Calculate the periodic interest by applying Formula 9.1.
Step 3:
Calculate the number of compound periods by applying Formula 9.2.
Step 4:
Calculate the maturity value by applying Formula 9.3.
Perform
Step 2:
\[i=\dfrac{9 \%}{4}=2.25 \%=0.0225 \nonumber \]
Step 3:
\[N=4 \times 10=40 \nonumber \]
Step 4:
\[FV=\$ 5,000(1+0.0225)^{40}=\$ 12,175.94 \nonumber \]
Calculator Instructions
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 40 | 9 | -5,000 | 0 | Answer: $ 12,175.94 | 4 | 4 |
After 10 years, the principal grows to $12,175.94, which includes your $5,000 principal and $7,175.94 of compound interest.
Future Value Calculations with Variable Changes
What happens if a variable such as the nominal interest rate, compounding frequency, or even the principal changes somewhere in the middle of the transaction? Formula 9.3 produces the correct final answer only when all variables remain unchanged. To illustrate this situation, assume your company modified its employee assistance plan one year after the money was borrowed, changing the interest rate in the second year from 12% compounded semi-annually to 12% compounded quarterly. Now how do you calculate the future value?
When any variable changes, you must break the timeline into separate time fragments at the point of the change. This timeline format is similar to those used in Section 8.1, involving variable simple interest rates. The timeline illustrates the employee's new scenario.
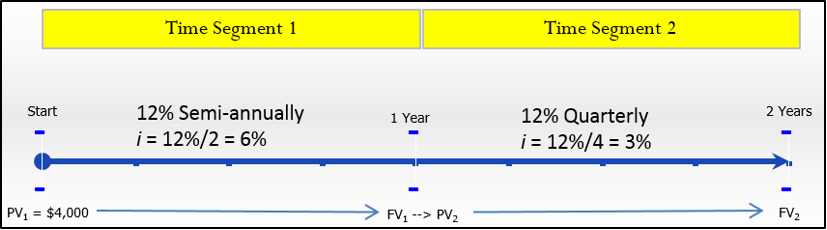
Figure \(\PageIndex{3}\)
Solving for the unknown \(FV\) on the right of the timeline means that you must start at the left side of the timeline. To arrive at the solution, you need to work from left to right one time segment at a time using Formula 9.3. As noted on the timeline, at the one-year point the future value of the first time segment then becomes the present value for the second time segment since the interest is not just accrued but actually placed into the account.
How It Works
Follow these steps when variables change in calculations of future value based on lump-sum compound interest:
Step 1: Read and understand the problem. Identify the present value. Draw a timeline broken into separate time segments at the point of any change. For each time segment, identify any principal changes, the nominal interest rate, the compounding frequency, and the length of the time segment in years.
Step 2: For each time segment, calculate the periodic interest rate (\(i\)) using Formula 9.1.
Step 3: For each time segment, calculate the total number of compound periods (\(N\)) using Formula 9.2.
Step 4: Starting with the present value in the first time segment (starting on the left), solve Formula 9.3.
Step 5: Let the future value calculated in the previous step become the present value for the next step. If the principal changes, adjust the new present value accordingly.
Step 6: Using Formula 9.3, calculate the future value of the next time segment.
Step 7: Repeat steps 5 and 6 until you obtain the final future value from the final time segment.
In the employee's new situation, he has borrowed $4,000 for two years with 12% compounded semi-annually in the first year and 12% compounded quarterly in the second year.
Step 1: Figure \(\PageIndex{3}\) shows a timeline. In time segment one, \(PV_1 = $4,000\), \(IY = 12\%\), \(CY = 2\), and the time segment is one year long. In time segment two, the only change is \(CY = 4\).
Step 2: In the first time segment, the periodic interest rate is \(i_{1}=12 \% / 2=6 \%\). In the second time segment, the periodic interest rate is \(i_{2}=12 \% / 4=3 \%\).
Step 3: The first time segment is one year long; therefore, \(N_{1}=2 \times 1=2\). The second time segment is also one year long; therefore, \(N_{2}=4 \times 1=4\).
Step 4: Apply Formula 9.3 to the first time segment:
\[FV_{1}=PV\left(1+i_{1}\right)^{N 1}=\$ 4,000(1+0.06)^{2}=\$ 4,494.40 \nonumber \]
Step 5: Let \(FV_{1}=\$ 4,494.40=PV_{2}\).
Step 6: Apply Formula 9.3 to the second time segment:
\[FV_{2}=PV_{2}\left(1+i_{2}\right)^{N 2}=\$ 4,494.40(1+0.03)^{4}=\$ 4,494.40 \times 1.03^{4}=\$ 5,058.49 \nonumber \]
Step 7: You reach the end of the timeline. The employee needs to repay $5,058.49 to clear the loan.
To perform the above steps on the calculator:
| Segment | N | I/Y | PV | PMT | FV | C/Y | P/Y |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 12 | 4000 | 0 | Answer: -4,494.40 | 2 | 2 |
| 2 | 4 | \(\surd\) | 4494.40 | \(\surd\) | Answer: -5,058.49 | 4 | 4 |
Note: A \(\checkmark\) that the value is already entered and does not need to be re-keyed into the calculator.
Important Notes
The BAII Plus Calculator:
Transforming the future value from one time segment into the present value of the next time segment does not require re-entering the computed value. Instead, apply the following technique:
- Load the calculator with all known compound interest variables for the first time segment.
- Compute the future value at the end of the segment.
- With the answer still on your display, adjust the principal if needed, change the cash flow sign by pressing the ± key, and then store the unrounded number back into the present value button by pressing PV. Change the N, I/Y, and C/Y as required for the next segment.
- Return to step 2 for each time segment until you have completed all time segments.
Things To Watch Out For
When you draw timelines, it is critical to recognize that any change in any variable requires a new time segment. This applies to changes in principal, the nominal interest rate, or the compounding frequency.
Paths To Success
Compound interest on a single payment is linked to the concept of percent change in Section 3.1. Every time interest is compounded and added to the principal, the periodic rate is the percent change in the principal. To use the percent change function on the calculator, assign \(\text { Old }=PV, \text { New }=FV, \Delta \%=i\), and \(\# PD=N\). The following two-step sequence shows the percent change function applied to the working example of the employee's new loan situation.
| Segment | OLD | NEW | %CH | #PD |
|---|---|---|---|---|
| 1 | 4000 | Answer: $4,494.40 | 6 | 2 |
| 2 | 4494.40 | Answer: $5,058.49 | 3 | 4 |
This is an alternative way to use the calculator to compute the future value of lump-sum amounts using compound interest.
- Which of the following investments involving the same principal results in the highest maturity value? Assume equal terms at each interest rate.
- 8% compounded annually followed by 6% compounded semi-annually
- 8% compounded semi-annually followed by 6% compounded semi-annually
- 8% compounded monthly followed by 6% compounded quarterly
- 8% compounded annually followed by 6% compounded quarterly
- How many time segments are involved in an investment where the successive interest rates are 9% compounded quarterly, 9% compounded monthly, 8% compounded monthly, and 9% compounded quarterly?
- Answer
-
- (iii) results in the largest maturity value. It has the highest compounding frequency in the first time segment and is tied for the highest compounding frequency in the second time segment.
- Four time segments are involved. Each change of interest rate requires a new time segment.
Five years ago Coast Appliances was supposed to upgrade one of its facilities at a quoted cost of $48,000. The upgrade was not completed, so Coast Appliances delayed the purchase until now. The construction company that provided the quote indicates that prices rose 6% compounded quarterly for the first 1½ years, 7% compounded semi-annually for the following 2½ years, and 7.5% compounded monthly for the final year. If Coast Appliances wants to perform the upgrade today, what amount of money does it need?
Solution
Take the original quote and move it into the future with the price increases. You can view this as a single lump sum with multiple successive interest rates. The amount of money needed today is the maturity amount (\(FV\)).
What You Already Know
Step 1:
The timeline below shows the original quote from five years ago until today.
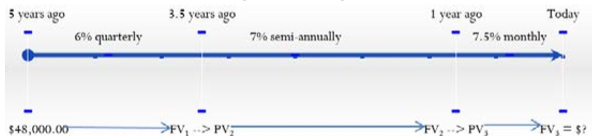
The principal, terms, and interest rates are known: \(PV_1\) = $48,000
First time segment: \(IY\) = 6%; \(CY\) = quarterly = 4 Term = 1½ years
Second time segment: \(IY\) = 7%; \(CY\) = semi-annually = 2 Term = 2½ years
Third time segment: \(IY\) = 7.5%; \(CY\) = monthly = 12 Term = 1 year
How You Will Get There
Step 2:
For each time segment, calculate the periodic interest rate by applying Formula 9.1.
Step 3:
For each time segment, calculate the number of compound periods by applying Formula 9.2.
Step 4/5:
Calculate the future value of the first time segment using Formula 9.3. Let \(FV_1 = PV_2\).
Step 6/5:
Calculate the future value of the second time segment using Formula 9.3. Let \(FV_2 = PV_3\). Repeat
Step 6/7:
Calculate the future value of the third time segment using Formula 9.3. \(FV_3\) is the final future value amount.
Perform
Step 2:
First segment: \(i=\dfrac{6 \%}{4}=1.5 \%\)
Second segment: \(i=\dfrac{7 \%}{2}=3.5 \%\)
Third segment: \(i=\dfrac{7.5 \%}{12}=0.625 \%\)
Step 3:
First segment: \(N=4 \times 1\tfrac{1}{2}=6\)
Second segment: \(N=2 \times 2\tfrac{1}{2}=5\)
Third segment: \(N=12 \times 1=12\)
Step 4/5:
First segment: \(FV_{1}=\$ 48,000 \times(1+0.015)^{6}=\$ 52,485.27667\)
Step 6/5:
Second segment: \(FV_{2}=\$ 52,485.27667 \times(1+0.035)^{5}=\$ 62,336.04435\)
Step 6/7:
Third segment: \(FV_{3}=\$ 62,336.04435 \times(1+0.00625)^{12}=\$ 67,175.35\)
Calculator Instructions
| Segment | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 6 | 6 | 48000 | 0 | Answer: -52,485.27677 | 4 | 4 |
| 2 | 5 | 7 | -52,485.27677 | \(\surd \) | Answer: -62,336.04435 | 2 | 2 |
| 3 | 12 | 7.5 | -62,336.04435 | \(\surd \) | Answer: -67,175.35 | 12 | 12 |
Coast Appliances requires $67,175.35 to perform the upgrade today. This consists of $48,000 from the original quote plus $19,175.35 in price increases.
Paths To Success
When you calculate the future value of a single payment for which only the interest rate fluctuates, it is possible to find the maturity amount in a single multiplication:
\[FV=PV \times\left(1+i_{1}\right)^{N_{1}} \times\left(1+i_{2}\right)^{N_{2}} \times \ldots \times\left(1+i_{n}\right)^{N_{n}}\nonumber \]
where \(n\) represents the time segment number. Note that the technique in Example \(\PageIndex{2}\) calculates each of these multiplications one step at a time, whereas this adaptation solves all time segments simultaneously. In the example above, you can calculate the same maturity value as follows:
\[FV=\$ 48,000 \times(1.015)^{6} \times(1.035)^{5} \times(1.0625)^{12}=\$ 67,175.35 \nonumber \]
Two years ago Lorelei placed $2,000 into an investment earning 6% compounded monthly. Today she makes a deposit to the investment in the amount of $1,500. What is the maturity value of her investment three years from now?
Solution
Take the original investment and move it into the future with the additional contribution. The amount of money three years from today is the maturity amount (\(FV\)).
What You Already Know
Step 1:
The timeline for this investment is below.
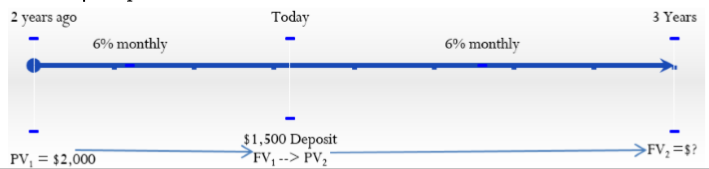
First time segment: \(PV_1\) = $2,000, \(IY\) = 6%, \(CY\) = 12, Years = 2
Second time segment: Deposit = $1,500, \(IY\) = 6%, \(CY\) = 12, Years = 3
How You Will Get There
Step 2:
For each time segment, calculate the periodic interest rate by applying Formula 9.1.
Step 3:
For each time segment, calculate the number of compound periods by applying Formula 9.2.
Step 4:
Calculate the future value of the first time segment using Formula 9.3.
Step 5:
Let \(FV_1 = PV_2\). Increase \(PV_2\) by the additional contribution amount of $1,500.
Step 6:
Calculate the future value of the second time segment using Formula 9.3.
Step 7:
\(FV_2\) is the final future value amount.
Perform
Step 2:
First segment: \(i=\dfrac{6 \%}{12}=0.5 \%\)
Second segment: \(i=\dfrac{6 \%}{12}=0.5 \%\)
Step 3:
First segment: \(N=12 \times 2=24\)
Second segment: \(N=12 \times 2=24\)
Step 4:
First segment: \(FV_{1}=\$ 2,000 \times(1+0.005)^{24}=\$ 2,254.319552\)
Step 5:
First segment: \(\$ 2,254.319552+\$ 1,500=\$ 3,754.319552=PV_{2}\)
Step 6:
Second segment: \(FV_{2}=\$ 3,754.319552 \times(1+0.005)^{36}=\$ 4,492.72\)
Calculator Instructions
| Segment | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 24 | 6 | -2000 | 0 | Answer: 2,254.319552 | 12 | 12 |
| 2 | 36 | \(\surd \) | -3,754.319552 | \(\surd \) | Answer: 4,492.721092 | \(\surd \) | \(\surd \) |
Three years from now Lorelei will have $4,492.72. This represents $3,500 of principal and $992.72 of compound interest.
Ruth purchased her $5,465 diamond ring four years ago through a payment plan offered by the jeweller. This plan did not require any regular payments within the four years; however, the balance including interest must be paid in full by the end of the fourth year to avoid a large financial penalty. During the four-year period, a quarterly compounded variable interest rate was charged. Initially, the interest was 8.75% before increasing to 9.25% after two years and then 9.75% after 3¼ years. She made two payments of $2,000 each, the first nine months after the purchase and the second after 3¼ years. What is the balance that she must pay at the end of the four years so that she doesn't incur any financial penalties?
Solution
Take Ruth’s initial purchase and charge it interest over the course of the four years while applying her payments to the principal at the appropriate points. Calculate the balance owing after four years; this is the future value (\(FV\)).
What You Already Know
Step 1:
The timeline is below.
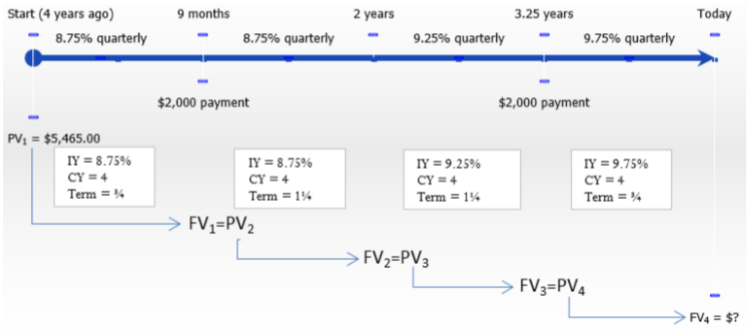
First time segment: \(PV_1\) = $5,465, \(IY\) = 8.75%, \(CY\) = 4, Years = ¾
Second time segment: Payment = $2,000, \(IY\) = 8.75%, \(CY\) = 4, Years = 1¼
Third time segment: \(IY\) = 9.25%, \(CY\) = 4, Years = 1¼
Fourth time segment: Payment = $2,000, \(IY\) = 9.75%, \(CY\) = 4, Years = ¾
How You Will Get There
Step 2:
For each time segment, calculate the periodic interest rate by applying Formula 9.1.
Step 3:
For each time segment, calculate the number of compound periods by applying Formula 9.2.
Step 4:
Calculate the future value of the first time segment using Formula 9.3.
Step 5:
Let \(FV_1 = PV_2\). Decrease \(PV_2\) by the $2,000 payment.
Step 6:
Calculate the future value of the 2nd time segment using Formula 9.3.
Repeat Step 5: Let \(FV_2 = PV_3\).
Repeat Step 6: Calculate the future value of the third time segment using Formula 9.3.
Repeat Step 5: Let \(FV_3 = PV_4\). Decrease \(PV_4\) by the $2,000 payment.
Repeat Step 6: Calculate the future value of the fourth time segment using Formula 9.3.
Step 7:
\(FV_4\) is the final future value amount.
Perform
Step 2:
First segment: \(i=\dfrac{8.75 \%}{4}=2.1875 \%\)
Second segment: \(i=\dfrac{8.75 \%}{4}=2.1875 \%\)
Third segment: \(i=\dfrac{9.25 \%}{4}=2.3125 \%\)
Fourth segment: \(i=\dfrac{9.75 \%}{4}=2.4375 \%\)
Step 3:
First segment: \(N=4 \times \dfrac{3}{4}=3\)
Second segment: \(N=4 \times 1\tfrac{1}{4}=5\)
Third segment: \(N=4 \times 1\tfrac{1}{4}=5\)
Fourth segment: \(N=4 \times \dfrac{3}{4}=3\)
Step 4:
First segment: \(FV_{1}=\$ 5,465 \times(1+0.021875)^{3}=\$ 5,465 \times 1.021875^{3}=\$ 5,831.543094\)
Step 5:
First segment: \(\$ 5,831.543094-\$ 2,000.00=\$ 3,831.543094=PV_{2}\)
Step 6:
Second segment: \(FV_{2}=\$ 3,831.543094 \times(1+0.021875)^{5}=\$ 4,269.358126\)
Step 5-6:
Third segment: \(FV_{3}=\$ 4,269.358126 \times(1+0.023125)^{5}=\$ 4,786.36782\)
Step 5:
Third segment: \(\$ 4,786.36782-\$ 2,000.00=\$ 2,786.36782=PV_{4}\)
Step 6:
Fourth segment: \(FV_{4}=\$ 2,786.36782 \times(1+0.024375)^{3}=\$ 2,995.13\)
| Segment | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| 1 | 3 | 8.75 | 5465 | 0 | Answer: -5,831.543094 | 4 | 4 |
| 2 | 5 | \(\surd \) | 3831.543094 | \(\surd \) | Answer: -4, 269.358126 | \(\surd \) | \(\surd \) |
| 3 | \(\surd \) | 9.25 | 4269.358126 | \(\surd \) | Answer: -4,786.36782 | \(\surd \) | \(\surd \) |
| 4 | 3 | 9.75 | 2786.36782 | \(\surd \) | Answer: -2,995.13 | \(\surd \) | \(\surd \) |
At the end of the four years, Ruth still owes $2,995.13 to pay off her ring.


