11.5: Number Of Annuity Payments
- Page ID
- 22135
How long do you require to fulfill the goal of your annuity? It all depends on your annuity payment, interest rate, and the amount of money involved.
When saving up for future goals, many people and businesses simply determine how much they can afford to invest each time period and then try to be patient until they meet their savings goal. What they do not know is how long it will take them. If you can put $75 per month into your vacation fund, how long will it take to save up the $1,000 needed for a spring break vacation in Puerto Vallarta?
Credit cards require a small minimum payment each month. A lot of Canadians view this minimum payment as a benefit and pay it without understanding what their decision implies. But interest rates on credit cards are around 21% compounded daily! So you can hardly afford to delay in paying off your credit card debt. Yet if you always make only the minimum monthly payment, extinguishing a $5,000 balance will take approximately 50 years!
Evidently the number of annuity payments is critical to financial transactions. In this section, you calculate the term of annuities by figuring out the number of annuity payments required.
Ordinary Annuities and Annuities Due
You must calculate the number of annuity payments in a variety of scenarios:
- Savings planning
- Debt extinguishment
- Sustaining withdrawals from an investment
A typical timeline used in calculating the term of an annuity appears below. Recall that N is not illustrated in the timeline but is calculated through Formula 11.1 using Years and \(PY\), which do appear on the timeline. The payment frequency, \(PY\), is a choice determined by the parties involved in the transaction and therefore is always known. That leaves Years, or the term of the annuity, as the unknown variable on the timeline. If you calculate N then you can also calculate Years using a rearrangement of Formula 11.1.

At either end of the timeline, only one of \(PV_{DUE}\), \(PV_{ORD}\), \(FV_{DUE}\), or \(FV_{ORD}\) will be known.
The Formula
Recall that the number of annuity payments, \(N\), is one of the variables in Formula 11.2, Formula 11.3, Formula 11.4, and Formula 11.5. Calculating this amount then requires you to substitute the known variables and rearrange the formula to solve for \(N\). Since \(N\) is located in the exponent, the rearrangement and isolation demands the usage of natural logarithms (see Section 2.6). The most difficult part is figuring out which formula you need to use. Choose the formula using the same decision criteria explained in Section 11.4 (under “The Formula”).
How It Works
Follow these steps, to solve for the number of annuity payments or the annuity term:
Step 1: Identify the annuity type. Draw a timeline to visualize the question.
Step 2: Identify the variables that always appear, including \(PMT, IY, CY\), and \(PY\). You must also identify one of the known values of \(PV_{ORD}\), \(PV_{DUE}\), \(FV_{ORD}\), or \(FV_{DUE}\).
Step 3: Use Formula 9.1 to calculate \(i\).
Step 4: Substitute into the correct annuity payment formula that matches your annuity type and known present or future value. Select from Formula 11.2, Formula 11.3, Formula 11.4, or Formula 11.5. Rearrange and solve for \(N\).
Step 5: To convert \(N\) back to a more commonly expressed format, such as years and months, take Formula 11.1 and rearrange it for Years. If Years is a decimal number, recall the steps required for converting to common language from "Integer Compounding Periods" on page xx in Section 9.7.
Important Notes
Dealing with Decimals in \(N\)
At the end of step 4, the calculated value of \(N\) may have decimals. Start by applying the same rounding rules involving the computation of \(N\) for single payments, mentally rounding the decimal off to the third decimal place.
- If the three decimals are zeroes, then the decimals are most likely a result of a rounded \(FV, PV\), or \(PMT\), so treat the \(N\) like an integer (ignoring the decimals).
- If the three decimals are not all zeroes, then \(N\) must always be rounded up to the next integer regardless of the decimal value. You must never round it down, because the calculated value of \(N\) represents the minimum payments required. The interpretation and implications of this rounding are as follows:
- Payments on a Debt. Assume your loan payments are $100 and you calculate \(N\) = 9.4, which rounds up to 10 payments. The payments must exactly reduce the loan to a balance of zero. The first nine payments are all $100. The last payment is not a complete payment, hence the 0.4 in the calculation. The precise calculation of this last payment amount is explained in Chapter 13; however, at this point it is sufficient to treat the decimal as an approximate percentage of what the final payment might be. The 0.4 is approximately 40% of $100, or $40. As a result, there are nine $100 payments, and one final payment approximating $40. Keep in mind that this approximation is rough at best and should only be used to get a feel for what the final payment amount could be. The important point here is that it requires 10 payments to pay off the loan completely, regardless of the amount of the payment.
- Payments toward an Investment. Keeping the numbers the same as above, your investment payments are $100 with \(N\) = 9.4. Again, this is 10 payments. If you only make nine full payments of $100, your investment will be short of your intended future value. However, if you let it grow and make the tenth full payment, you will have more than your investment goal. What the \(N\) = 9.4 is telling you is that a final tenth payment is needed roughly 40% of the way through the next payment interval that is approximately 0.4 of the regular payment amount. However, most investors don't care about having too much money saved and exceeding their savings goal, so usually a full tenth payment is made.
Things To Watch Out For
Two mistakes are common in calculations of the number of annuity payments:
- Misinterpreting \(N\). Confusing the compounding frequency (\(CY\)) and payment frequency (\(PY\)) results in the misinterpretation of \(N\) and the incorrect calculation of the term. Since \(N\) represents the number of annuity payments, to assign its meaning you need to look at the \(PY\), not the \(CY\). Then use the value of \(PY\) in Formula 11.1 when expressing \(N\) in more common terms. For example, if \(N\) = 8, \(PY\) = 4, and \(CY\) =2, a common mistake is to say that there are eight semi-annual payments (using the \(CY\)); ensure you look instead at the \(PY\), identifying the eight quarterly payments, which means the term is two years.
- Confusing the Term and the Last Payment on Annuities Due. One of the characteristics of an annuity due is that the last payment occurs one payment interval before the end of the term of the annuity. When you calculate \(N\), you have calculated the term of the annuity. The last payment occurs \(N − 1\) intervals from the start of the annuity. For example, assume payments are monthly and you calculate \(N = 12\) months. This means the term of the annuity is 12 months. The last payment on the annuity due is 12 – 1 = 11 months from the start. In your “Plan” for any problem, be sure to recognize whether you are looking for the end of the term or when the last payment is made. This problem does not occur for ordinary annuities since the last payment and the end of the term are on the same date.
Holding all other variables constant, what happens mathematically to the number of payments (the precise calculated value of \(N\) produced by rearranging any of the annuity formulas) if the following occur:
- The variable interest rate increases (and the payment itself remains unchanged)?
- The annuity payments are doubled?
- Answer
-
- The number of payments increases if the variable interest rate increases since more interest is charged but the payment has not increased to cover the higher interest charges.
- The number of payments is normally cut at least by half if the annuity payments are doubled since with each payment the principal becomes smaller at an accelerated rate and less interest is charged.
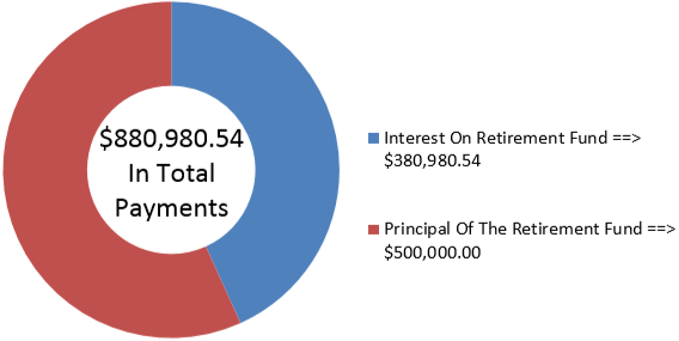
Samia has $500,000 accumulated in her retirement savings when she decides to retire at age 60. If she wants to receive beginning-of-month payments of $3,000 and her retirement annuity can earn 5.2% compounded monthly, how old is Samia when the fund is depleted?
Solution
Step 1:
The payments are at the beginning of the payment intervals, and the compounding period and payment intervals are the same. Therefore, this is a simple annuity due. In looking for how old Samia will be when the fund is depleted, calculate the number of annuity payments, or \(N\), that her retirement annuity can sustain.
What You Already Know
Step 1 (continued):
The timeline for the retirement annuity appears below.

Step 2:
\(PV_{DUE}\) = $500,000, \(IY\) = 5.2%, \(CY\) = 12, \(PMT\) = $3,000, \(PY\) = 12, \(FV\) = 0
How You Will Get There
Step 3:
Apply Formula 9.1.
Step 4:
Substitute into Formula 11.5, rearranging for \(N\).
Step 5:
Substitute into Formula 11.1 and solve for Years. Add this term to Samia’s current age to figure out how old she is when the annuity is depleted.
Perform
Step 3:
\[i=5.2 \% \div 12=0.4 \overline{3} \% \nonumber \]
Step 4:
\[\$ 500,000=\$ 3,000\left[\dfrac{1-\left[\frac{1}{(1+0.0043)^{\frac{12}{12}}}\right]^N}{(1+0.004 \overline{3})^{\frac{12}{12}}-1}\right] \times(1+0.004 \overline{3})^{\frac{12}{12}} \nonumber \]
\[\begin{aligned} 165.947560&=\dfrac{1-0.995685^{N}}{0.0043}\\ 0.995685^{N}&=0.280893 \\ N \times \ln (0.995685)&=\ln (0.280893)\\ N&=\dfrac{-1.2697323}{-0.004323}\\ N&=293.660180 \end{aligned} \nonumber \]
Rounding up to 294 monthly payments consisting of 293 regular payments plus one additional smaller payment.
Step 5:
\[294=12 \times \text { Years } \nonumber \]
\[\text { Years }=\dfrac{294}{12}=24.5=24 \text { years, } 6 \text { months } \nonumber \]
Calculator Instructions
| Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| BGN | Answer: 293.660180 | 5.2 | -500000 | 300 | 0 | 12 | 12 |
The figure shows how much principal and interest make up the payments. If Samia is currently 60 years old and the annuity endures for 24 years and six months, then she will be 84.5 years old when the annuity is depleted. Note that Samia will receive 293 payments of $3,000 along with a smaller final payment that is approximated by taking 66.018% × $3,000 = $1,980.54
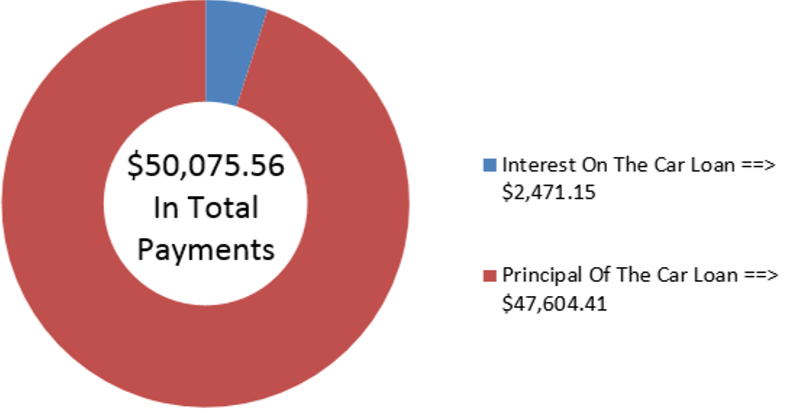
Brendan is purchasing a brand new Mazda MX-5 GT. Including all options, accessories, and fees, the total amount he needs to finance is $47,604.41 at the dealer's special interest financing of 2.4% compounded monthly. If he makes payments of $1,000 at the end of every month, how long will it take to pay off his car loan?
Solution
Step 1:
The payments are at the end of the payment intervals with a monthly compounding period and monthly payment intervals. Therefore, this is an ordinary simple annuity. Calculate the number of monthly payments, or \(N\), to figure out the length of time required to pay off the loan.
What You Already Know
Step 1 (continued):
The timeline for the car payments appears below.

Step 2:
\(PV_{ORD}\) = $47,604.41, \(IY\) = 2.4%, \(CY\) = 4, \(PMT\) = $1,000, \(PY\) = 12, \(FV\) = 0
How You Will Get There
Step 3:
Apply Formula 9.1.
Step 4:
Substitute into Formula 11.4, rearranging for \(N\).
Step 5:
Substitute into Formula 11.1 and solve for Years.
Perform
Step 3:
\[i=2.4 \% \div 12=0.2 \% \nonumber \]
Step 4:
\[\begin{aligned} \$ 47,604.41&=\$ 1,000\left[\dfrac{1-\left[\dfrac{1}{(1+0.002)^{\frac{12}{12}}}\right]^{N}}{(1+0.002)^{\frac{12}{12}-1}}\right] \\ 0.095208&=1-0.998003^{N} \\ 0.998003^N&=0.904791\\ N \times \ln (0.998003)&=\ln (0.904791) \\ N&=\dfrac{-0.100051}{-0.001998}\\ &=50.075560 \end{aligned} \nonumber \]
Rounded up to 51 monthly payments.
Step 5:
\[51=12 \times \text { Years } \nonumber \]
\[\text { Years }=\dfrac{51}{12}=4.25=4 \text { years, } 3 \text { months } \nonumber \]
Calculator Instructions
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| Answer: 50.075560 | 2.4 | 47604.41 | -1000 | 0 | 12 | 12 |
The figure shows how much principal and interest make up the payments. To own his vehicle, Brendan will make payments for four-and-a-quarter years. This consists of 50 payments of $1,000 and a smaller final payment that is approximated by taking 7.556% × $1,000 = $75.56.
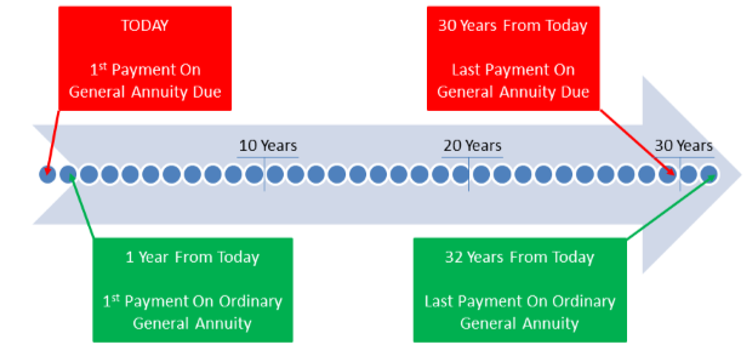
Trevor wants to save up $1,000,000. He will contribute $5,000 annually to an investment earning 10% compounded monthly. What is the time difference between his last payments (not the end of the annuities) if he makes his contributions at the end of the year instead of at the beginning of the year?
Solution
Step 1:
In this question you are being asked to compare two annuities that differ in their payment intervals and their compounding periods. One annuity makes contributions at the beginning of the interval, while the other makes contributions at the end. Therefore, you must contrast one general annuity due with one ordinary general annuity. To determine the time difference, calculate N for each annuity and compare when the last payment is made.
What You Already Know
Step 1 (continued):
A combined timeline for the two annuities appears below.

Step 2:
Ordinary general annuity: \(FV_{ORD}\) = $1,000,000, \(IY\) = 10%, \(CY\) = 12, \(PMT\) = $5,000, \(PY\) = 1
General annuity due: \(FV_{DUE}\) = $1,000,000, \(IY\) = 10%, \(CY\) = 12, \(PMT\) = $5,000, \(PY\) = 1
How You Will Get There
Step 3:
Apply Formula 9.1.
Step 4:
Apply Formula 11.2 and Formula 11.3, rearranging for \(N\).
Step 5:
If payments are annual, then \(N\) = Years. However, for the general annuity due the last payment is made \(N − 1\) years from today. The difference between the two payments can then be calculated.
Step 3:
\[i=10 \% \div 12=0.8 \overline{3} \% \nonumber \]
Step 4:
Ordinary general annuity:
\[\begin{aligned} \$ 1,000,000&=\$ 5,000\left[\dfrac{\left[(1+0.008 \overline{3})^{\frac{12}{1}}\right]^{N}-1}{(1+0.008 \overline{3})^{\frac{12}{1}}-1}\right]\\ 20.942613&= 1.104713^{N}-1 \\ 21.942613&=1.104713^{N}\\ \ln (21.942613) & = N \times \ln (1.104713) \\ \dfrac{\ln (21.942613)}{\ln (1.104713)}&=N \\ N&=31.012812, \text { or } 32 \text { years } \end{aligned} \nonumber \]
General annuity due:
\[\begin{aligned} \$ 1,000,000&=\$ 5,000\left[\dfrac{\left[(1+0.008 \overline{3})^{\frac{12}{1}}\right]^{N}-1}{(1+0.008 \overline{3})^{\frac{12}{1}}-1}\right]\times (1+0.008 \overline{3})^{\frac{12}{1}}\\ 18.957514&= 1.104713^{N}-1 \\ 19.957514&=1.104713^{N}\\ \ln (19.957514) & = N \times \ln (1.104713) \\ \dfrac{\ln (19.957514)}{\ln (1.104713)}&=N \\ N&=30.060618, \text { or } 31 \text { years } \end{aligned} \nonumber \]
Step 5:
The ordinary general annuity last payment is 32 years from today. The general annuity due has a term of 31 years, but the last payment is 31 − 1 = 30 years from today. The difference between the last payments is 32 − 30 = 2 years sooner. (See the figure below and count the dots!)
Calculator Instructions
| Type | Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|---|
| Ordinary | Answer: 30.060618 | 10 | 0 | -5000 | 1000000 | 1 | 12 | |
| Due | BGN | Answer: 31.012812 | \(\surd\) | \(\surd\) | \(\surd\) | \(\surd\) | \(\surd\) | \(\surd\) |
In order for Trevor to reach his goal, if he were to make his $5,000 contributions at the beginning of the year (that is, under the annuity due) instead of the end of the year (under the ordinary annuity), his last payment would be two years sooner. Do not confuse this with the terms of the two annuities, which end only one year apart (31 years from now and 32 years from now).