11.4: Annuity Payment Amounts
- Page ID
- 22134
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Whether you are acquiring merchandise and property or saving up toward some future goal, you will deal with annuity payments. When you graduate college and land that promising entry-level position with your employer, a lot of demands are going to get placed on your limited income. If you do not already own a place of your own, perhaps you will get one. This means the purchase of a starter home for which you will make monthly mortgage payments. To fill that home, acquiring some furniture and electronics might take you to The Brick, Sleep Country Canada, Best Buy, or The Home Depot. Then you may be staggered by all the home maintenance items you need. If you make a lot of purchases all at once, you will probably take advantage of various payment plans. These place even more demands on your monthly income. Do not forget that you will need some wheels too. You can either lease or purchase a car. Great, another payment to make! Finally, you remember what your math instructor taught you about the importance of getting started early on your RRSP, so you should begin making those monthly contributions soon, too.
Will you have enough income to cover all of your payments? Unlike the many consumers who must rely on retailers and banks to figure out their payments, your study of annuity payments will allow you to calculate the amounts yourself.
Businesses also make annuity payments for a wide variety of purposes. Whether saving up for future corporate goals or acquiring products and property, businesses have regular bills, too. Marketers develop payment plans for their consumers. Financial agents make investments involving periodic payments. Companies issue marketable bonds that require regular interest payments to investors. Human resource personnel look after employee benefits, including RRSP contributions and pension plan payments. Production departments need expensive machinery, so they must keep payment plans within operating budgets. No matter your choice of profession, as a business manager you will encounter annuity payment calculations.
Ordinary Annuities and Annuities Due
You need to calculate an annuity payment in many situations:
- Figuring out loan or mortgage payments
- Determining membership or product payment plans
- Calculating lease payments
- Determining the periodic payment necessary to achieve a savings goal
- Determining the maximum payment that an investment annuity can sustain over a period of time
A typical timeline for solving for an annuity payment amount appears in the next figure. All variables except for the payment amount (\(PMT\)) are known. While the figure shows all the possible variables and their location on the timeline, the following should be noted at each end of the timeline:

- If the \(PV_{DUE}\) or \(PV_{ORD}\) is known on the left, then \(FV\) is the only variable that may appear on the right. \(FV_{DUE}\), \(FV_{ORD}\), and \(PV\) are variables that will not appear on the timeline.
- If the \(FV_{DUE}\) or \(FV_{ORD}\) is known on the right, then \(PV\) is the only variable that may appear on the left. \(PV_{DUE}\), \(PV_{ORD}\), and \(FV\) are variables that will not appear on the timeline.
The Formula
Recall that the annuity payment amount, \(PMT\), is one of the variables in Formula 11.2, Formula 11.3, Formula 11.4, and Formula 11.5. Calculating this amount then requires you to substitute the known variables and rearrange the formula for PMT. The most difficult part of this process is figuring out which of the four formulas to use. Your selection depends on the two factors summarized in this table and discussed afterwards.
| Formula To Use | Annuity Payment Timing | Annuity Value Known |
|---|---|---|
| 11.2 | End | \(FV_{ORD}\) |
| 11.4 | End | \(PV_{ORD}\) |
| 11.3 | Beginning | \(FV_{DUE}\) |
| 11.5 | Beginning | \(PV_{DUE}\) |
- Are the annuity payments to be made at the beginning or at the end of the payment interval? In other words, do you have an annuity due or an ordinary annuity?
- Do you know the amount that the annuity starts or ends with? In other words, do you know the present value or future value of the annuity?
How It Works
Follow these steps to solve for any annuity payment amount:
- Step 1: Identify the annuity type. Draw a timeline to visualize the question.
- Step 2: Identify the variables that you know, including \(IY, CY, PY\), and Years. You must also identify a value for one of \(PV_{ORD}\), \(PV_{DUE}\), \(FV_{ORD}\), or \(FV_{DUE}\). You may or may not have a value for \(FV\) or \(PV\).
- Step 3: Use Formula 9.1 to calculate \(i\).
- Step 4: If a single payment \(PV\) or \(FV\) is known, move it to the other end of the time segment using Formula 9.3. To determine \(N\), apply Formula 9.2 since this is for a single payment, not an annuity. When you move the amount to the same focal date as the present or future value of the annuity, either add this number to the annuity value or subtract it as the situation demands. Example \(\PageIndex{3}\) later in this section will illustrate this practice.
- Step 5: Use Formula 11.1 to calculate \(N\). Apply the correct annuity payment formula that matches your annuity type and known present or future value. Select from Formula 11.2, Formula 11.3, Formula 11.4, or Formula 11.5 then rearrange for the annuity payment amount, \(PMT\). If you performed step 4 above, be sure to use the adjusted future or present value of your annuity in the formula.
Important Notes
When calculating loan payments, recall that the last payment is slightly different from all other payments. Chapter 13 explores how to calculate the last payment precisely. For the purposes of this section, treat the last payment like any other payment and assume it is equal to all the other payments when you make any statement about loan payment amounts or totals.
Things To Watch Out For
Should you grow or shrink a balance? Give some thought to the relationships between the present value, annuity payments, and future value.
- If somebody is contributing to an investment, the future value of the annuity should be larger than the total of all annuity payments.
- If somebody is receiving from an investment or making debt payments, the total of all annuity payments should exceed the present value.
- An investor has been making $1,000 annual contributions to his account for five years. In this problem, should the future value be more than, less than, or equal to $5,000?
- A debtor needs to make $1,000 annual payments on her loan for five years to extinguish her debt. In this problem, should the present value be more than, less than, or equal to $5,000?
- A retirement fund can make five annual payments of $1,000 before being extinguished. In this problem, should the present value be more than, less than, or equal to $5,000?
- Answer
-
- The future value will be more than $5,000. The payments earn interest.
- The present value will be less than $5,000. The payments represent the principal and interest together.
- The present value will be less than $5,000. The principal earns interest while paying out.
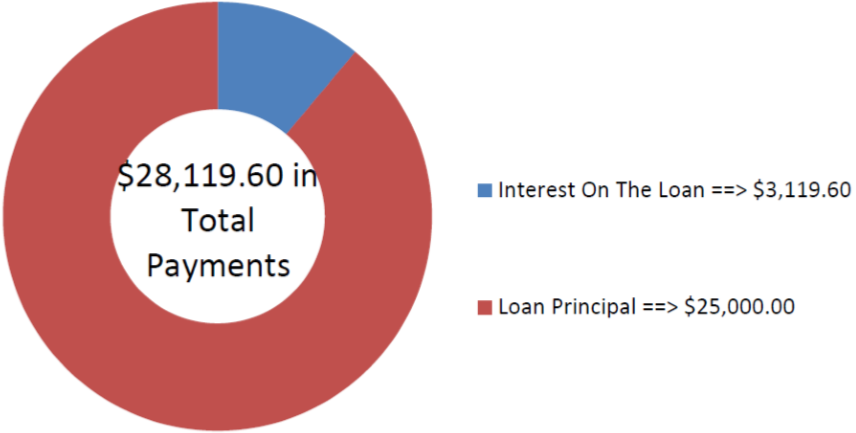
Morgan wants to consolidate a lot of smaller debts into a single three-year loan for $25,000. If the loan is charged interest at 7.8% compounded monthly, what is her payment amount at the end of every month?
Solution
Step 1:
The payments are made at the end of the payment intervals, and the compounding period and payment intervals are the same. Therefore, this is an ordinary simple annuity. Calculate the monthly amount of her loan payment, or \(PMT\).
What You Already Know
Step 1 (continued):
The timeline for the loan appears below.

Step 2:
\(PV_{ORD}\) = $25,000, \(IY\) = 7.8%, \(CY\) = 12, \(PY\) = 12, Years = 3, \(FV\) = $0
How You Will Get There
Step 3:
Apply Formula 9.1.
Step 4:
Since \(FV\) = $0, skip this step.
Step 5:
Apply Formula 11.1 and Formula 11.4, rearranging for \(PMT\).
Perform
Step 3:
\[i=7.8 \% \div 12=0.65 \% \nonumber \]
Step 5:
\(N=12 \times 3=36\) payments
\[\$ 25,000=PMT\left[\dfrac{1-\left[\frac{1}{(1+0.0065)^{\frac{12}{12}}}\right]^{36}}{(1+0.0065)^{\frac{12}{12}}-1}\right] \nonumber \]
\[PMT=\dfrac{\$ 25,000}{32.005957}=\$ 781.10 \nonumber \]
Calculator Instructions
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 36 | 7.8 | 25000 | Answer: -781.104587 | 0 | 12 | 12 |
The figure shows how much principal and interest make up the payments. To pay off her consolidated loan, Morgan's month-end payments for the next three years will be $781.10.
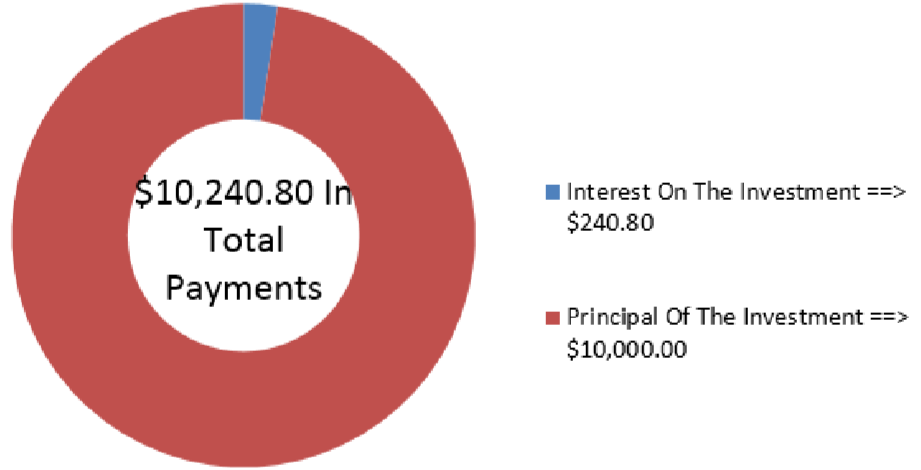
Franco has placed $10,000 into an investment fund with the goal of receiving equal amounts at the beginning of every month for the next year while he backpacks across Europe. If the investment fund can earn 5.25% compounded quarterly, how much money can Franco expect to receive each month?
Solution
Step 1:
The payments are at the beginning of the payment intervals, and the compounding period and payment intervals are different. Therefore, this is a general annuity due. Calculate the monthly amount he can receive, or \(PMT\).
What You Already Know
Step 1 (continued):
The timeline for the vacation money appears below.

Step 2:
\(PV_{DUE}\) = $10,000, \(IY\)= 5.25%, \(CY\)= 4, \(PY\)= 12, Years=1, \(FV\) = $0
How You Will Get There
Step 3:
Apply Formula 9.1.
Step 4:
Since \(FV\) = $0, skip this step.
Step 5:
Apply Formula 11.1 and Formula 11.3, rearranging for \(PMT\).
Perform
Step 3:
\[i=5.25 \% \div 4=1.3125 \% \nonumber \]
Step 5:
\(N=12 \times 1=12\) payments
\[\$ 10,000=PMT\left[\dfrac{1-\left[\frac{1}{(1+0.013125)^{\frac{4}{12}}}\right]^{12}}{(1+0.013125)^{\frac{4}{12}}-1}\right] \times(1+0.013125)^{\frac{4}{12}} \nonumber \]
\[PMT=\dfrac{\$ 10,000}{11.717849}=\$ 853.40 \nonumber \]
Calculator Instructions
| Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| BGN | 12 | 5.25 | -10000 | Answer: 853.398928 | 0 | 12 | 4 |
The figure shows how much principal and interest make up the payments. While backpacking across Europe, Franco will have his annuity pay him $853.40 at the beginning of every month.
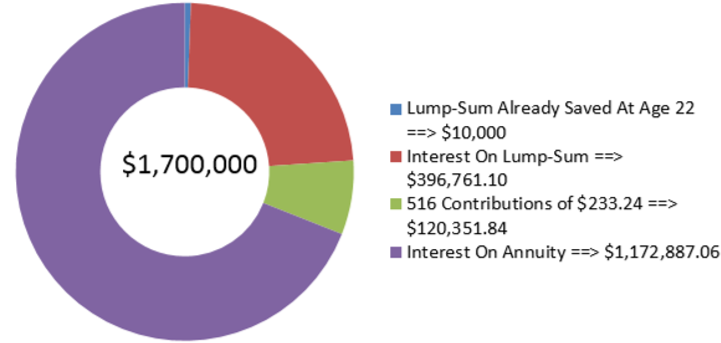
Kingsley's financial adviser has determined that when he reaches age 65, he will need $1.7 million in his RRSP to fund his retirement. Kingsley is currently 22 years old and has saved up $10,000 already. His adviser thinks that his RRSP will average 9% compounded annually throughout the years. To meet his RRSP goal, how much does Kingsley need to invest every month starting today?
Solution
Step 1:
The payments are made at the beginning of the payment intervals, and the compounding period and payment intervals are different. Therefore, this is a general annuity due. Calculate the monthly amount Kingsley needs to contribute, or PMT.
What You Already Know
Step 1 (continued):
The timeline for Kingsley’s RRSP contributions appears below.

Step 2:
\(PV\) = $10,000, \(FV_{DUE}\) = $1,700,000, \(IY\) = 9%, \(CY\) = 1, \(PY\) = 12, Years = 43
How You Will Get There
Step 3:
Apply Formula 9.1.
Step 4:
You need to move the present value to Kingsley’s age 65, the same date as \(FV_{DUE}\). Apply Formula 9.2 and Formula 9.3. The \(FV\) is money the annuity does not have to save, so you subtract it from \(FV_{DUE}\) to arrive at the amount the annuity must generate.
Step 5:
Apply Formula 11.1 and Formula 11.3, rearranging for \(PMT\), using the adjusted \(FV_{DUE}\).
Step 3:
\[i=9 \% \div 1=9 \% \nonumber \]
Step 4:
\(N=1 \times 43=43\) compounds
\[FV=\$ 10,000(1+0.09)^{43}=\$ 406,761.0984 \nonumber \]
\[\text { New } FV_{DUE}=\$ 1,700,000-\$ 406,761.0984=\$ 1,293,238.902 \nonumber \]
Step 5:
\(N=12 \times 43=516\) payments
\[\$ 1,293,238.902=PMT\left[\dfrac{\left((1+0.09)^{\frac{1}{12}}\right]^{516}-1}{(1+0.09)^{\frac{1}{12}}-1}\right) \times(1+0.09)^{\frac{1}{12}} \nonumber \]
\[PMT=\dfrac{\$ 1,293,238.902}{5,544.647665}=\$ 233.24 \nonumber \]
Calculator Instructions
| Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| BGN | 516 | 9 | -10000 | Answer: -233.240952 | 1700000 | 12 | 1 |
The figure shows how much principal and interest make up the final balance. To meet his retirement goals, Kingsley needs to invest $233.24 at the beginning of every month for the next 43 years. In doing so, he will achieve a $1.7 million balance in his account at age 65. (Note: Similar to loan payments, the last payment in actuality is required to be a slightly higher amount since the annuity payment was rounded downwards. However, the last payment is treated equally at this time for purposes of all calculations.)
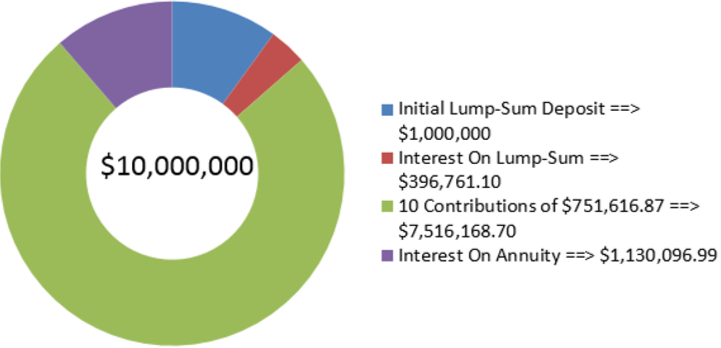
The production department just informed the finance department that in five years’ time the robotic systems on the production line will need to be replaced. The estimated cost of the replacement is $10 million. To prepare for this purchase, the finance department immediately deposits $1,000,000 into a savings annuity earning 6.15% compounded semi-annually, and it plans to make semi-annual contributions starting in six months. How large do those contributions need to be?
Solution
Step 1:
The payments are made at the end of the payment intervals, and the compounding period and payment intervals are the same. Therefore, this is an ordinary simple annuity. Calculate the monthly amount the finance department needs to contribute, or \(PMT\).
What You Already Know
Step 1 (continued):
The timeline for the machinery fund appears below.

Step 2:
\(PV\) = $1,000,000, \(FV_{ORD}\) = $10,000,000, \(IY\)= 6.15%, \(CY\)= 2, \(PY\)= 2, Years= 5
How You Will Get There
Step 3:
Apply Formula 9.1.
Step 4:
The present value must be moved to the five-year date, the same date as \(FV_{ORD}\). Apply Formula 9.2 and Formula 9.3.This \(FV\) is money the annuity does not have to save, so it is subtracted from \(FV_{ORD}\) to arrive at the amount the annuity must generate.
Step 5:
Apply Formula 11.1 and Formula 11.2, rearranging for \(PMT\), using the adjusted \(FV_{ORD}\).
Step 3:
\[i=6.15 \% \div 2=3.075 \% \nonumber \]
Step 4:
\(N=2 \times 5=10 \) compounds
\[FV=\$ 1,000,000(1+0.03075)^{10}=\$ 1,353,734.306 \nonumber \]
\[\text { New } FV_{ORD}=\$ 10,000,000-\$ 1,353,734.306=\$ 8,646,265.694 \nonumber \]
Step 5:
\(N=2 \times 5=10\) payments
\[\$ 8,646,265.694=PMT\left[\dfrac{\left[(1+0.03075)^{\frac{2}{2}}\right]^{10}-1}{(1+0.03075)^{\frac{2}{2}}-1}\right] \nonumber \]
\[PMT=\dfrac{\$ 8,646,265.694}{11.503554}=\$ 751,616.87 \nonumber \]
Calculator Instructions
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 10 | 6.15 | -1000000 | Answer: -751,616.8656 | 10000000 | 2 | 2 |
The figure shows how much principal and interest make up the final balance. To have adequate funding for the production line machinery replacement five years from now, the finance department needs to deposit $751,616.87 into the fund every six months. (Note: Similar to loan payments, the last payment in actuality is required to be a slightly lower amount since the annuity payment was rounded upwards. However, the last payment is treated equally at this time for purposes of all calculations.)