11.6: Annuity Interest Rates
- Page ID
- 22136
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Canada One RV advertises that you can purchase a Residence 40' Park Model trailer, valued at $32,999, for $181.84 biweekly over the next 10 years. Toronto Hyundai offers a "Smokin' Hot Deal" for a $9,900 Hyundai with $69 biweekly payments for seven years. Going online, you visit the 407 Express Toll Route (407 ETR) website to look at paying your tolls on this Toronto highway and see that you can pay $21.50 annually or $3.25 per month. Checking your vehicle registration, you see on the insurance website that you can pay your motorcycle insurance in a single payment of $2,667 or five beginning-of-month payments of $538. The question in all of these situations is, should you pay all at once or in installments?
Notice in all of these cases that the total of the payments is higher than the purchase price of the item. For example, the 407 ETR is billing $3.25 per month, totalling $39.00 per year! From a strictly financial perspective, the difference from the $21.50 can be treated like an amount of interest charged for not paying the full annual amount up front. But what interest rate are you paying?
In investing, you should choose the highest effective rate that carries a level of risk you can accept. If you make fixed contributions to an investment, what interest rate must you obtain to meet your future goal? On debts, do you know what you are being charged? That is your hard-earned money you are spending, so perhaps you can find a better offer at a lower rate from someone else? In business, debt interest is an expense that affects the pricing of products and is deductible from income tax. To calculate the interest, the business needs to know the interest rate it is being charged.
You have many reasons to calculate an annuity's interest rate. In this last section on annuities, you will make this calculation for both ordinary annuities and annuities due.
Ordinary Annuities and Annuities Due
You must calculate the interest rate on an annuity in a variety of situations:
- To determine the interest rate being charged on any debt
- To determine the interest rate that an investment is earning
- To calculate the required interest rate for savings to reach a goal within a certain time period
- To calculate the required interest rate needed for a series of payments to be sustained over a certain time period
A typical timeline for the unknown interest rate on an annuity appears in the figure below.

All variables must be known except for the nominal interest rate, \(IY\). At either end of the timeline:
- If you know \(PV_{DUE}\) or \(PV_{ORD}\), there might be an \(FV\) on the other side as well. \(FV_{DUE}\), \(FV_{ORD}\), and \(PV\) will not appear.
- If you know \(FV_{DUE}\) or \(FV_{ORD}\), there might be a \(PV\) on the other side. \(PV_{DUE}\), \(PV_{ORD}\), and \(FV\) will not appear.
The Formula
A most interesting circumstance arises when you attempt to solve any of the future value or present value annuity formulas, both ordinary and due, for the interest rate. Formula 11.2 is reprinted below for illustration; however, the same point holds for Formulas 11.3 to 11.5.
\[\text { Formula } 11.2: FV_{ORD}=PMT\left[\dfrac{\left[(1+i)^{\frac{CY}{PY}}\right]^{N}-1}{(1+i)^{\frac{CY}{PY}}-1}\right] \nonumber \]
In this formula, the \(FV_{ORD}\), \(PMT\), or \(N\) each appears only once. This allows you to easily manipulate the formula to solve for these variables, as we have done in previous sections. However, the periodic interest rate, \(i\), appears in the formula twice. This normally is not a problem because you can apply basic rules of algebra to isolate and combine like terms, but not so in this instance.
To illustrate the difficulty, assign \(PMT\) = $1 and make \(CY = PY\). That makes the equation look like this:
\[FV_{ORD}=\dfrac{(1+i)^N-1}{i} \nonumber \]
If you rearrange the formula you have
\[iFV_{ORD}+1=(1+i)^N \nonumber \]
The \(i\) on the left-hand side is free to be isolated, but the i on the right-hand side is part of the base for an exponent. To cancel the \(N\) exponent, you need to raise both sides of the equation to the exponent of \(1/N\), arriving at the following:
\[\left(iFV_{ORD}+1\right)^{\frac{1}{N}}=1+i \nonumber \]
Note the result: Now the left -hand side has \(i\) being part of a base for an exponent, while the \(i\) on the right-hand side is free to be isolated. Not much of an improvement, is it? To fix this, you will need to take both sides of the equation to the exponent of \(N\), which puts you back in your original dilemma. It is an endless loop with no solution.
The bottom line is that there is no algebraic way to isolate the \(i\) in this equation. Thus, no rearrangement of Formulas 11.2 to 11.5 to isolate this variable is possible. So how do you solve for it? There are two ways:
- Trial and Error. In this manual method, you simply keep plugging in various values for \(i\) and attempt to home in on the actual value for the variable. Perhaps you start with \(i\) = 1% and find out that your \(FV_{ORD}\) is too low. Then you try \(i\) = 2% and find out that your \(FV_{ORD}\) is too high. Now you know that i is between 1% and 2%, so perhaps you try 1.5%. You repeat this process until you end up with a precise enough number. As you can imagine, this process is extremely time consuming, tedious, and prone to errors, so no one performs this process by hand any more.
- Use Technology. Whether you use calculators or spreadsheets, these tools are pre-programmed with the trial-and-error technique and can perform millions of iterations in less than a second to find the solution. All problems in this section, therefore, assume you have access to technology, so no algebraic solutions appear in the formula calculations.
How It Works
Follow these steps to solve for any nominal interest rate:
Step 1: Identify the annuity type. Draw a timeline to visualize the question.
Step 2: Identify the variables that you know, including \(CY, PMT, PY\), and Years. You must also identify a value for one of \(PV_{ORD}\), \(PV_{DUE}\), \(FV_{ORD}\), or \(FV_{DUE}\). You may or may not have a value for \(FV\) or \(PV\).
Step 3: Use Formula 11.1 to calculate N. Input all six of the known variables into your technology and solve for the interest rate.
Important Notes
Solving for the nominal interest rate on your BAII+ requires you to enter all six of the other variables excluding the \(I/Y\). Then press CPT \(I/Y\) to solve the problem. Because of the trial-and-error technique, it may take your calculator a few seconds to compute the answer. If your screen goes blank and your calculator hesitates, this is normal! The values you enter in the present value (\(PV\)), future value (\(FV\)), and annuity payment (\(PMT\)) must adhere to the cash flow sign convention. Remember that on the BAII+, the \(I/Y\) represents the nominal interest rate, which is compounded according to the value you entered into the \(C/Y\) variable.
Things To Watch Out For
When solving for the interest rate, pay careful attention to which form of interest rate is being sought:
- Periodic (\(i\)): What is the interest rate per month?
- Nominal (\(IY\) with \(CY ≠ 1\)): What is the interest rate compounded monthly?
- Effective (\(IY\) with \(CY = 1\)): What is the annually compounded or effective rate of interest?
Paths To Success
If you want to know both the nominal and effective interest rate in any situation, there are two methods to produce the answers. The first step in both methods is to solve the problem for the nominal interest rate using the appropriate value for the compounding frequency (\(CY\)). Then to calculate the effective rate you can do one of the following:
- Change the \(CY\) to a value of one (\(CY = 1\)) and recalculate the \(IY\). This book prefers this method as it is the easier and less error-prone method.
- Take your calculated nominal interest rate and convert it to an effective interest rate by using Formula 9.4 (interest rate conversion), calculator (I Conv function), or the Chapter 9 Excel template (which uses the EFFECT function of Excel). This technique produces the same basic solution; however, it has a higher chance of error and may lack precision if not enough decimals are used.
Is it possible in financial situations for the calculated value of the nominal interest rate, \(IY\), to be negative?
- Answer
-
Yes, it is possible. Many investments such as stocks fluctuate based on market conditions. It is possible for an investment to lose its value after it is purchased, which produces a negative rate of return.
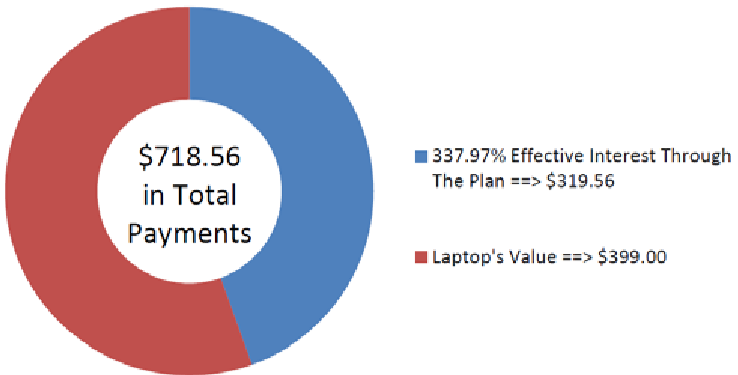
Smartchoice, a rent-to-own store, offers a Dell 10" Mini Inspiron Netbook for a cash n' carry price of $399. Alternatively, under its rent-to-own plan you could make $59.88 monthly payments in advance and own the laptop after one year. What interest rate is effectively being charged on the rent-to-own plan?
Solution
Step 1:
The payments are made at the beginning of the payment intervals, and the compounding period and payment intervals are different. Therefore, this is a general annuity due. Solve for the effective interest rate, which is the nominal interest rate, \(IY\), that has a compounding frequency of one.
What You Already Know
Step 1 (continued):
The timeline for the retirement annuity appears below.

Step 2:
\(PV_{DUE}\) = $399, \(CY\) = 1, \(PMT\) = $59.88, \(PY\) = 12, Years = 1
How You Will Get There
Step 3:
Apply Formula 11.1 and Formula 11.5. Enter the information into the calculator to solve for \(IY\) (which automatically applies Formula 9.1 to convert \(i\) to \(IY\)).
Perform
Step 3:
\(N=12 \times 1=12\) payments
\[\$ 399=\$ 59.88\left[\dfrac{1-\left[\dfrac{1}{(1+i)^{\frac{1}{12}}}\right]^{12}}{(1+i)^{\frac{1}{12}}-1}\right] \times(1+i) \frac{1}{12} \nonumber \]
See calculator instructions for the solution.
Calculator Instructions
| Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| BGN | 12 | Answer: 337.975924 | 399 | -59.88 | 0 | 12 | 1 |
The figure shows the effective interest and the laptop’s value that make up the payments. The effective interest rate being charged under the rent-to-own payment plan is 337.9759%.
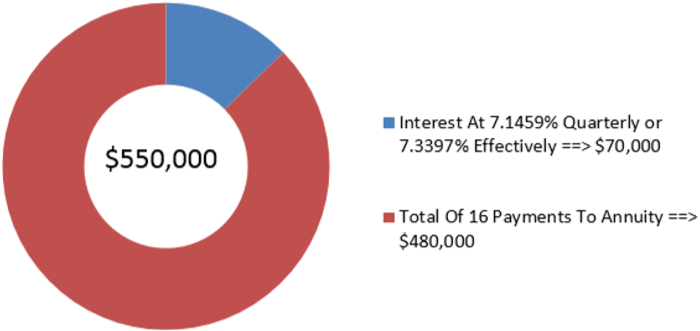
Cubonic Industries deposits $30,000 at the end of every quarter to save up $550,000 for a capital project in four years. To achieve its goal, what nominal interest rate compounded quarterly does Cubonic Industries require on its investment? What is the effective rate?
Solution
Step 1:
There are two questions here. The first question about the nominal interest rate involves an ordinary simple annuity. Solve this for \(IY\) when \(CY\) = 4. The second question about the effective rate involves an ordinary general annuity. Solve this for \(IY\) when \(CY\) = 1.
What You Already Know
Step 1 (continued):
The timeline for both questions appears below.

Step 2:
Ordinary simple annuity: \(FV_{ORD}\) = $550,000, \(CY\) = 4, \(PMT\) = $30,000, \(PY\) = 4, Years = 4
Ordinary general annuity: All the same except \(CY\) = 1
How You Will Get There
Step 3:
Apply Formula 11.1 and Formula 11.2.
Ordinary simple annuity: Enter the information into the calculator and solve for \(IY\).
Ordinary general annuity: Change the \(CY\) to 1 (for the effective rate) and recalculate \(IY\). Note that for both annuities the calculator automatically applies Formula 9.1 to convert \(i\) to \(IY\).
Perform
Step 3:
\(N=4 \times 4=16\) payments
Ordinary Simple Annuity:
\[\$ 550,000=\$ 30,000\left[\dfrac{\left[(1+i)^{\frac{4}{4}}\right]^{16}-1}{(1+i)^{\frac{4}{4}}-1}\right] \nonumber \]
Ordinary General Annuity :
\[\$ 550,000=\$ 30,000\left[\dfrac{\left[(1+i)^{\frac{1}{4}}\right]^{16}-1}{(1+i)^{\frac{1}{4}}-1}\right] \nonumber \]
See the calculator instructions below for the solution to each question.
Calculator Instructions
| Type | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| Simple | 16 | Answer: 7.145908 | 0 | -30000 | 550000 | 4 | 4 |
| General | \(\surd\) | Answer: 7.339689 | \(\surd\) | \(\surd\) | \(\surd\) | \(\surd\) | 1 |
The figure shows how much principal and interest make up the final balance. For Cubonic Industries to achieve its savings goal, the savings annuity must earn 7.1459% compounded quarterly, or 7.3397% effectively.
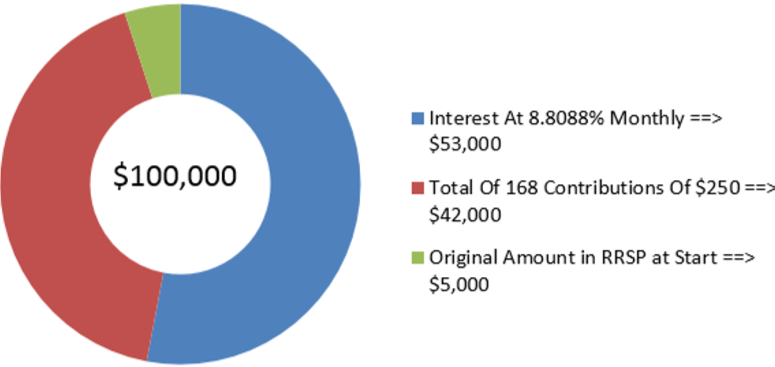
Amadeus has already saved $5,000 in his RRSP today. Suppose he continues to make $250 contributions at the beginning of each month for the next 14 years. For him to achieve his goal of having $100,000, what monthly nominal rate of return must his investment earn?
Solution
Step 1:
The payments are made at the beginning of the payment intervals, and the compounding period and payment intervals are the same. Therefore, this is a simple annuity due. Solve for the monthly nominal interest rate, \(IY\).
What You Already Know
Step 1 (continued):
The timeline for RRSP contributions appears below.

Step 2:
\(FV_{DUE}\) = $100,000, \(PV\) = $5,000, \(CY\) =12, \(PMT\) = $250, \(PY\) = 12, Years = 14
How You Will Get There
Step 3:
Apply Formula 11.1 and the calculator simultaneously solves Formulas 9.3 and 11.3. The annuity is simple, so \(N\) is the same number for both the number of payments and compounds. Enter the information into the calculator and solve for \(IY\).
Perform
Step 3:
\(N=12 \times 14=168\) payments
\[\$ 100,000-\$ 5,000(1+i)^{168}=\$ 250\left[\dfrac{\left[(1+i)^{\frac{12}{12}}\right]^{168}-1}{(1+i)^{\frac{12}{12}}-1}\right] \times(1+i)^{\frac{12}{12}} \nonumber \]
See the calculator instructions for the solution.
Calculator Instructions
| Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|
| BGN | 168 | Answer: 8.808808 | -5000 | -250 | 100000 | 12 | 12 |
The figure shows how much principal and interest make up the final balance. The nominal rate of interest that Amadeus must earn on his investment is 8.8088% compounded monthly.
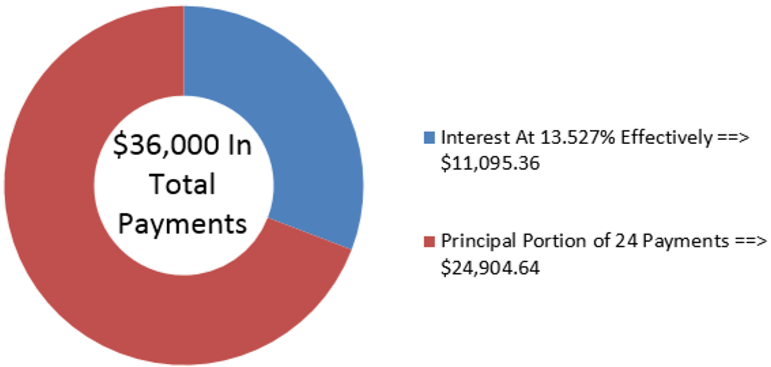
Gemma is looking to purchase a new Nissan Pathfinder for $54,904.64 including all fees and sales taxes. She can afford to pay no more than $1,500 at the end of every month, and she wants to have the balance owing reduced to $30,000 after two years, when she can pay off the vehicle with her trust fund. What is the maximum effective rate of interest she could be charged on the car loan to meet her goals?
Solution
Step 1:
The payments are made at the end of the payment intervals, and the compounding period and payment intervals are different. Therefore, this is an ordinary general annuity. Solve for the effective interest rate, \(IY\).
What You Already Know
Step 1 (continued):
The timeline for the car loan appears below.

Step 2:
\(PV_{ORD}\) = $54,904.64, \(FV\) = $30,000, \(CY\) =1, \(PMT\) = $1,500, \(PY\) = 12, Years = 2
How You Will Get There
Step 3:
Apply Formula 11.1, and the calculator simultaneously solves Formulas 9.3 and 11.4. *Note that since the annuity is general, the \(N\) compounds and \(N\) payments are different numbers. Putting these two elements into the same equation requires that \(N\) take on a single value equaling the number of payments (the annuity requirement). In this regard, the periodic interest rate used in Formula 9.3 must be converted to match the payment frequency. You accomplish this using the same \(\dfrac{CY}{PY}\) exponent from the annuities formulas. Enter the information into the calculator and solve for \(IY\).
Perform
Step 3:
\(N=12 \times 2=24\) payments
\[\$ 54,904.64-\dfrac{\$ 30,000}{\left[(1+i)^{\frac{1}{12}}\right]^{24}}=\$ 1,500\left[\dfrac{1-\left[\frac{1}{(1+i)^{\frac{1}{12}}}\right]^{24}}{(1+i)^{\frac{1}{12}}-1}\right] \nonumber \]
See the calculator instructions for the solution.
Calculator Instructions
| N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|
| 24 | Answer: 13.527019 | 54904.64 | -1500 | -30000 | 12 | 1 |
The figure shows how much principal and interest make up the payments. Gemma will be able to purchase the car if she can obtain a car loan that has an effective interest rate lower than 13.527%.