13.4: Special Application - Mortgages
- Page ID
- 22148
If you buy a home in Canada, you will almost certainly need to take out a mortgage. After all, the expense is huge: on average a house costs $784,567 in Vancouver, $432,576 in Calgary, $261,666 in Winnipeg, $503,094 in Toronto, $272,069 in Halifax, and $318,363 in the Northwest Territories!1 As mentioned earlier in this book, the average Canadian home costs approximately $378,369.2 Compare that with Canadian median family gross income of $69,860,3 and once you consider the income left after all deductions and expenses it becomes obvious that you will have to pay for your home gradually over many years. That means you must make use of a financial institution’s money over time, all the while paying for this privilege in the form of interest.
Your home mortgage may well be the biggest personal financial transaction you will ever make, so understanding the factors that determine your mortgage payments can save you a lot of money. This section explains mortgage fundamentals and shows you how to amortize and calculate payments on various mortgages.
Mortgages Explained
This figure illustrates the various concepts related to mortgages. Each of these concepts is discussed below.
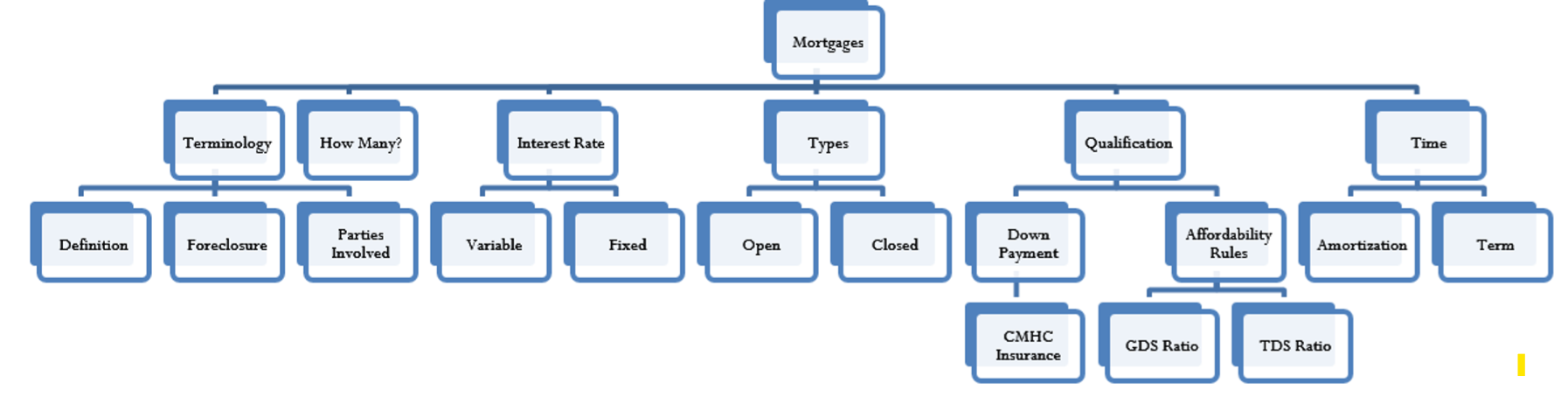
Terminology
A mortgage is a special type of loan that is collaterally secured by real estate. In essence, the loan has a lien against the property, that is, the right to seize the property for the debt to be satisfied. An individual or business taking out a mortgage is obliged to pay back the amount of the loan with interest based on a predetermined contract. The financial institution, though, has a claim on the real estate property in the event that the mortgage goes into default, meaning that it is not paid as per the agreement. In these instances, financial institutions will pursue foreclosure of the property, which allows for the tenants to be evicted and the property to be sold. The proceeds of the sale are then used to pay off the mortgage. A mortgage always involves two parties. The individual or business that borrows the money is referred to as the mortgagor, and the financial institution that lends the money is referred to as the mortgagee.
How Many Mortgages
A real estate property can have more than one mortgage. The main mortgage based on the amount of money borrowed to purchase the home is called the first mortgage. But property owners can choose to have other mortgages as well. For example, most home equity lines of credit (HELOCs) are secured by a second mortgage against the property. Sometimes homeowners borrow money to make home improvements or renovations and have these amounts placed as an additional mortgage against the property. Any number of mortgages against a property is possible, though it is uncommon to have more than three. The order of the mortgages is important. If the mortgage goes into default and foreclosure occurs, the mortgagee with the first mortgage gets access to the proceeds first. If any money is left over after the first mortgage is paid off, the mortgagee of the second mortgage gets the remainder. If anything is left, the third mortgagee gets the balance and so on until all proceeds have been expended. Ultimately, any money left over after all mortgages and costs have been paid belongs to the mortgagor.
Interest Rate
In the mortgage contract, the two parties can agree to either a fixed interest rate or a variable interest rate. Either way, the mortgage always forms an ordinary annuity since interest is not payable in advance.
- Under a fixed interest rate, the principal is repaid through a number of equal payments that cover both the interest and principal components of the loan. The interest portion is highest at the beginning and gradually declines over the amortization period of the mortgage. In Canada, fixed interest rates are either annually or semi-annually compounded; the latter is the prevailing choice.
- In a variable interest rate mortgage, the principal is repaid through an agreed-upon number of unequal payments that fluctuate with changes in borrowing rates. The principal and interest portions of the payment vary as interest rates fluctuate, meaning that the interest portion can rise at any point with any increase in rates. When rates change, a common practice in many financial institutions is to change the variable interest rate as of the first day of the next month. If the rate change does not coincide with a mortgage payment date, then the interest portion is calculated in a way similar to the procedure for a demand loan (see Section 8.5), where the exact number of days at the different rates must be determined. In Canada, variable interest rates are usually compounded monthly.
Types of Mortgages
The mortgage agreement can be open or closed. An open mortgage has very few rules and it allows the mortgagor to pay off the debt in full or make additional prepayments at any given point in any amount without penalty. A closed mortgage has many rules that determine how the mortgage is to be paid. It does not allow the mortgager to pay off the debt in full until the loan matures. As a marketing tool, most closed mortgages have “top-up” options that allow the mortgagor to make additional payments (such as an additional 20% per year) against the mortgage without penalty. Any payments exceeding the maximums or early payment of the mortgage are penalized heavily, with a three-month minimum interest charge that could be increased up to a measure called the interest rate differential, which effectively assesses the bank's loss and charges the mortgagor this full amount.
Qualification
Purchasing a home and obtaining a mortgage requires a down payment. You can get a mortgage with a 25% down payment or more; this is known as a loan-to-value ratio of 75% or less. The loan-to-value ratio divides the principal borrowed by the value of the house. If you do not have enough down payment to meet this criterion, you can make the real estate purchase with as little as 5% down (a 95% loan-to-value ratio); however, your mortgage must then be insured by the Canada Mortgage and Housing Corporation (CMHC). The premium charged for the insurance can range from 0.5% to 3.3% of the principal borrowed, depending on the mortgage particulars.
To qualify for a mortgage, you must also meet two affordability rules:
- The first affordability rule states that your principal, interest, taxes, and heating expenses, or PITH, must not exceed 32% of your gross monthly household income. If the real estate involves a condominium, then 50% of the condo fees are also included in the PITH. This is known as the gross debt service (GDS) ratio.
- The second affordability rule states that the PITH plus all other debt requirements must not exceed 40% of gross monthly household income. Other debt can include any other debt payments such as car loans, credit cards, or student loans. This is known as the total debt service (TDS) ratio.
It is important to note that these ratios have some degree of flexibility depending on the financial institution issuing the mortgage. Each of the percentages for the ratios commonly varies by up to ±3% depending on the particular institution’s policies.
Time
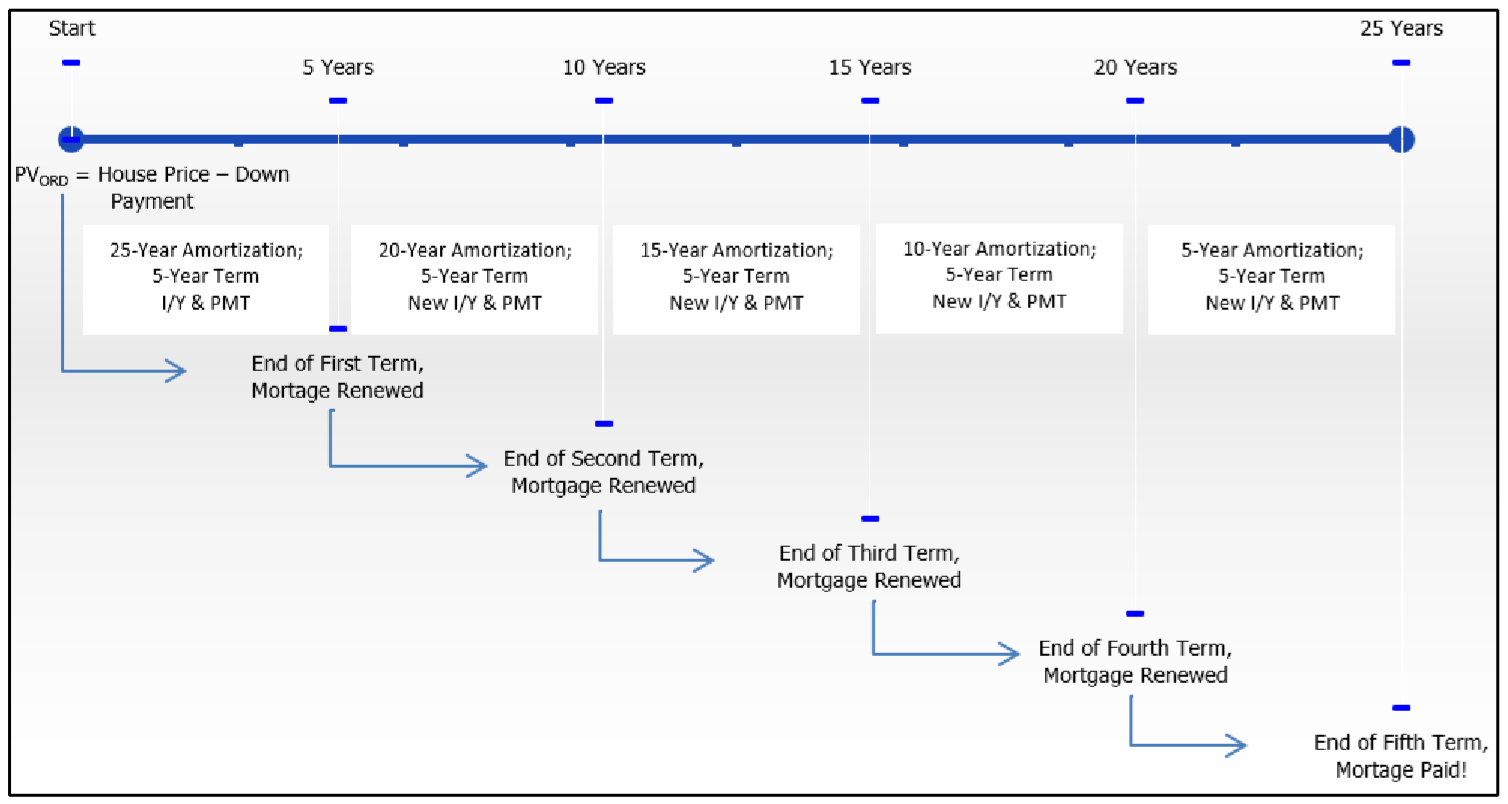
Finally, due to the large amount of principal borrowed in a real estate purchase, the mortgage may be amortized over an extended time period. The most common amortization is 25 years with a maximum of 30 years. That is a long time frame for any contract. Consequently, mortgages are taken out in shorter terms, usually up to no more than five years, although some institutions do offer seven- or ten-year terms. This allows the financial institution regular opportunities to update the interest rate to reflect current mortgage rates. What this means to the mortgagor is that the mortgage becomes due in full at the end of each term. Most people then renew their mortgage for another term, though the amortization period becomes shorter in accordance with the number of years elapsed since the initial principal was borrowed. The figure below illustrates the typical mortgage amortization process, where the amortization is initially established at 25 years and the mortgagor uses five consecutive five-year terms to pay off the debt.
How Mortgage Interest Rates Are Determined
The actual interest rate you can obtain on a mortgage is determined by five factors in combination:
- The Bank of Canada Rate. This rate sets the basis from which all variable rates are determined. The prime rate (the Bank of Canada rate +2%) is usually the lowest obtainable interest rate. Some banks, however, discount this rate slightly by a margin between 0.1% and 0.4%.
- Bond Market Rates. Bond market rates set the basis for which all fixed interest rates are determined. Fluctuations in the prime rate do not necessarily affect bond market rates.
- The Mortgage Type. Open mortgages have substantially higher rates than equivalent closed mortgages because of the uncertainty of when the mortgage will be paid off. Banks protect their interests and minimize the risks of open mortgages through the higher rate.
- The Term. As the length of the term increases, the interest rate increases as well. This is due to the uncertainty of future interest rates. The financial institution must protect itself against rising rates in the future.
- The Type of Rate. Variable rates are lower than fixed rates since the financial institution can adjust the rate at any time to match prevailing conditions. Fixed rates do not share this benefit of adjustability and therefore are higher to protect the financial institution.
The table on the next page illustrates some actual posted semi-annually compounded interest rates at the time of writing.
| Term | Closed Mortgage | Open Mortgage | ||
|---|---|---|---|---|
| Variable Rate | Fixed Rate | Variable Rate | Fixed Rate | |
| 1 year | 2.10% | 3.09% | 3.14% | 6.30% |
| 5 year | 3.00% | 5.34% | 4.00% | 8.25% |
Calculating the Mortgage Payment
The following mortgage variables are always known:
- Mortgage interest rates are posted by every financial institution. The posted rate is almost always negotiable, and a smart mortgagor may be able to negotiate up to a 1% deduction from the posted rate.
- The mortgagor chooses the amortization period, the term, and the payment frequency and also negotiates these variables with the financial institution.
- The principal is determined by the value of the home purchased less any down payment plus any fees or premiums.
- All mortgages are ordinary annuities.
What is left? The unknown variable is the mortgage payment amount that matches the time value of money variables. When calculating this amount, the most important variable is the amortization period, which determines the length of time over which the loan is repaid. It forms the basis for calculating the payment. Note that the term has no effect on the payment calculation. It dictates only the time frame during which the current mortgage arrangement (interest rate, payment frequency, type, and so on) remains in effect.
How It Works
Follow these steps to calculate a mortgage payment:
Step 1: Visualize the mortgage by drawing a timeline as illustrated below. Identify all other time value of money variables, including \(PV_{ORD}, IY, CY, PY\), and Years. The future value, \(FV\), is always zero (the mortgage is repaid).
Step 2: Calculate the periodic interest rate (\(i\)) using Formula 9.1.
Step 3: Calculate the number of annuity payments (\(N\)) using Formula 11.1. Remember to use the amortization period and not the term for the Years variable in this calculation.
Step 4: Calculate the ordinary annuity payment amount using Formula 11.4 and rearranging for \(PMT\). You must round this calculated amount to two decimals since it represents a physical payment amount.
In each of the following situations determine which mortgage results in a higher mortgage payment. Assume all other time value of money variables remain constant.
- Open or closed
- Fixed or variable
- Two-year fixed rate or five-year fixed rate
- Ten-year amortization or 20-year amortization
- Answer
-
- Open (open mortgages always have a higher interest rate than closed mortgages).
- Fixed rates are always higher to account for future uncertainties.
- Five-year fixed rate (the longer the term, the higher the rate).
- Ten-year amortization (there is less time to pay off the debt, meaning higher payments are required).
The Olivers are looking to purchase a new home from Pacesetter Homes in a northeastern Calgary suburb. An Appaloosa 3 model show home can be purchased for $408,726.15. They are planning on putting $50,000 as a down payment with a 25 year amortization and weekly payments. If current mortgage rates are fixed at 5.29% compounded semi-annually for a five year closed term, determine the mortgage payment required.
Solution
Calculate the mortgage payment amount required (\(PMT\)).
What You Already Know
Step 1:
The mortgage timeline appears below.
\(PV_{ORD}\) = $408,726.15 − $50,000 = $358,726.15, \(IY\) = 5.29%, \(CY\) = 2, \(PY\) = 52, Years = 25, \(FV\) = $0
How You Will Get There
Step 2:
Apply Formula 9.1.
Step 3:
Apply Formula 11.1.
Step 4:
Calculate the mortgage payment using Formula 11.4, rearranging for \(PMT\).
Perform
Step 2:
\[i=5.29 \% / 2=2.645 \% \nonumber \]
Step 3:
\(N=52 \times 25=1,300\) payments
Step 4:
\[\$ 358,726.15=PMT\left[\dfrac{1-\left[\dfrac{1}{(1+0.02645)^{\frac{2}{52}}}\right]^{1300}}{(1+0.02645)^{\frac{2}{52}}-1}\right] \nonumber \]
\[PMT=\dfrac{\$ 358,726.15}{\left[\dfrac{1-\left[\dfrac{1}{1.001004}\right]^{1,300}}{0.001004}\right]}=\$ 494.40 \nonumber \]
Calculator Instructions
| Mode | N | I/Y | PV |
|---|---|---|---|
| END | 1300 | 5.29 | 358726.15 |
| PMT | FV | P/Y | C/Y |
|---|---|---|---|
| Answer: -494.398328 | 0 | 52 | 2 |
If the Olivers purchase this home as planned, they are mortgaging $358,726.15 for 25 years. During the first five-year term of their mortgage, they make weekly payments of $494.40. After the five years, they must renew their mortgage.
Renewing the Mortgage
When the term of a mortgage expires, the balance remaining becomes due in full. Typically the balance owing is still quite substantial, so the mortgage must be renewed. As discussed earlier, this means that the mortgagor assumes another mortgage, not necessarily with the same financial institution, and the amortization term is typically reduced by the length of the first term. The length of the second term of the mortgage then depends on the choice of the mortgagor. Other variables such as payment frequency and the interest rate may or may not change.
For example, assume a mortgage is initially taken out with a 25-year amortization and a five-year term. After five years, the mortgage becomes due in full. Unable to pay it, the mortgagor renews the mortgage for the remaining 20-year amortization, and also opts for a three-year term in assuming the new mortgage. When those three years are over, the mortgagor renews the mortgage for the remaining 17-year amortization and again makes another term decision. This process repeats until the debt is ultimately paid off.
How It Works
Follow these steps to renew a mortgage:
Steps 1 to 4: The steps for calculating the mortgage payment amount remain unchanged.
Step 5: Determine the balance remaining at the end of the mortgage term. This involves the following:
- Calculate the future value of the mortgage principal (\(FV\)) at the end of the term using Formulas 9.2 (Number of Compounding Periods for Single Payments) and 9.3 (Compound Interest for Single Payments).
- Calculate the future value of the mortgage payments (\(FV_{ORD}\)) made throughout the term using Formulas 11.1 (Number of Annuity Payments) and 11.2 (Future Value of an Ordinary Annuity).
- Calculate the remaining balance by taking \(FV − FV_{ORD} = BAL\).
Step 6: Depending on the information being sought, repeat the above steps as needed for each mortgage renewal using the new amortization remaining, the new interest rate, any changes in payment frequency, and the new term. For example, if you are looking for the mortgage payment in the second term, repeat just steps 2 through 4. If looking for the balance remaining at the end of the second term, repeat step 5 as well.
Important Notes
Most commonly, mortgagors progress along the original path of amortization with each mortgage term renewal. The mortgaging process does not require this, though. With any renewal, the mortgagor may choose either to shorten or to lengthen the amortization period. If shortening the amortization period causes no TDS or GDS ratio concerns, the mortgagor can pay off the mortgage faster. If the mortgagor wishes to lengthen the amortization period, the financial institution may look at the overall time to pay the debt and put an upper cap on how long the amortization period may be increased.
Things To Watch Out For
The most common mistake with mortgages is to confuse the term and the amortization period. Remember:
- When you determine the mortgage payment amount, you use the amortization period to determine the \(N\).
- When you calculate the balance remaining at the end of a mortgage period, you use the term to determine the \(N\).
Paths To Success
When you use your BAII Plus calculator to calculate the remaining balance at the end of the term, you can arrive at this number in one of two ways. Once you have computed the mortgage payment amount and re-entered it into the calculator with only two decimals, you determine the last payment number for the mortgage term and then either
- Input this value into the \(N\) and solve for \(FV\), or
- Open up the AMORT function and input the last payment number into both P1 and P2. Scroll down to BAL for the solution.
A mortgage was taken out in its first term with a semi-annually compounded interest rate of 6%. If the mortgage remains on the same amortization schedule, what happens to the mortgage payment if the new semi-annually compounded interest rate upon renewal is
- 6.5%
- 5.5%
- 6%
- Answer
-
- PMT rises, since more interest is charged to the mortgage.
- PMT falls, since less interest is charged to the mortgage.
- PMT remains the same, since there is no change in the interest charged to the mortgage.
The Chans purchased their home three years ago for $389,000 less a $38,900 down payment at a fixed semi-annually compounded rate of 4.9% with monthly payments. They amortized the mortgage over 20 years. The Chans will renew the mortgage on the same amortization schedule at a new rate of 5.85% compounded semi-annually. How much will their monthly payments increase in the second term?
Solution
Calculate the original mortgage payment in the first term, or \(PMT_1\). Then renew the mortgage and recalculate the mortgage payment in the second term, or \(PMT_2\). The amount by which \(PMT_2\) is higher is their monthly payment increase.
What You Already Know
Step 1:
The Chans’s mortgage timeline appears below.
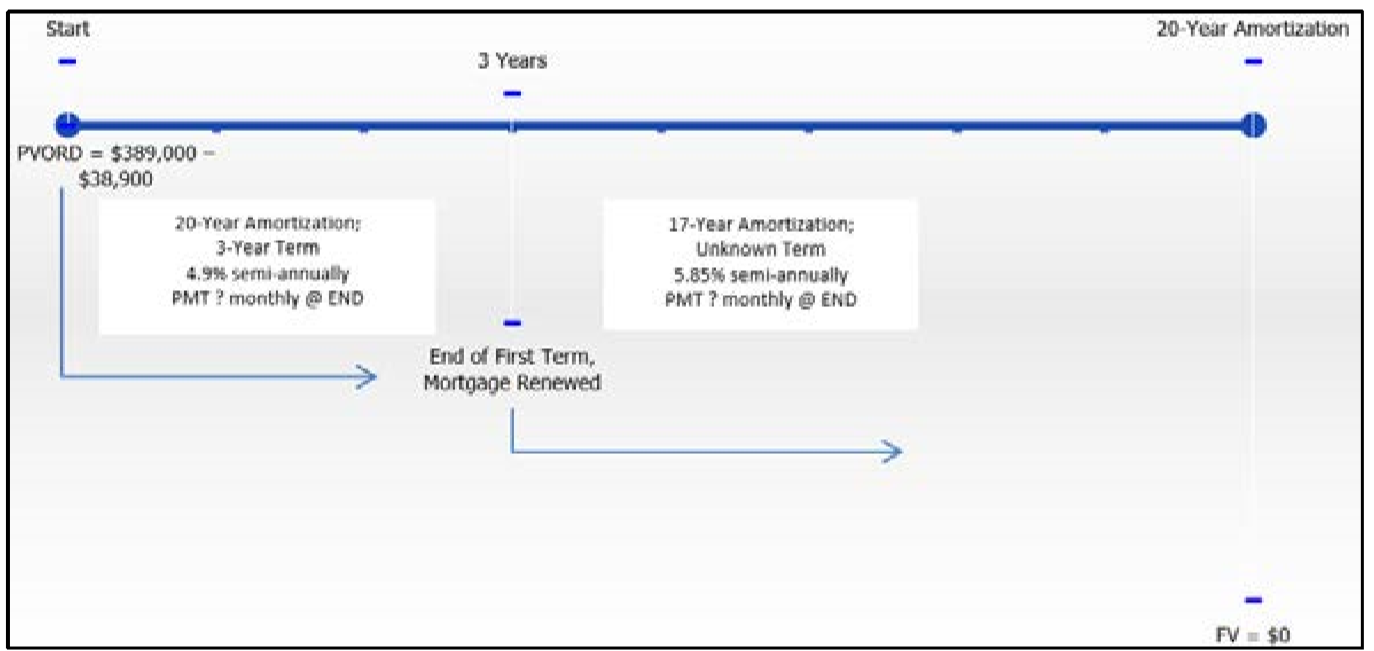
First Term: \(PV_{ORD}\) = $389,000 − $38,900 = $350,100, \(IY\) = 4.9%, \(CY\) = 2, \(PY\) = 12, Years = 20, \(FV\) = $0
Second Term: \(PV_{ORD} = BAL\) after first term, \(IY\) = 5.85%, \(CY\) = 2, \(PY\) = 12, Years = 17, \(FV\) = $0
How You Will Get There
Step 2:
For the first term, apply Formula 9.1.
Step 3:
For the first term, apply Formula 11.1.
Step 4:
For the first term, calculate the mortgage payment using Formula 11.4, rearranging for \(PMT\).
Step 5:
Calculate the future value of the principal at the end of the first term using Formulas 9.2 and 9.3 for the principal and Formulas 11.1 and 11.2 for the mortgage payments. Determine the remaining balance through \(BAL = FV − FV_{ORD}\).
Step 6:
Calculate the new mortgage payment through Formulas 9.1, 11.1, and 11.4, rearranging for \(PMT\).
Step 7:
Calculate the increase from the first to the second payment.
Perform
Step 2:
\[i=4.9 \% / 2=2.45 \% \nonumber \]
Step 3:
\(N=12 \times 20=240\) payments
Step 4:
\[\$ 350,100=PMT\left[\dfrac{1-\left[\dfrac{1}{(1+0.0245)^{\frac{2}{12}}}\right]^{240}}{(1+0.0245)^{\frac{2}{12}}-1}\right] \nonumber \]
\[PMT=\dfrac{\$ 350,100}{\left[\dfrac{1-\left[\dfrac{1}{1.004042}\right]^{240}}{0.004042}\right]}=\$ 2,281.73 \nonumber \]
Step 5:
Principal:
\(N=2 \times 3=6\) compounds; \(FV=\$ 350,100(1+0.0245)^{6}=\$ 404,821.7959\)
Payments:
\(N=12 \times 3=36 \) payments
\[FV_{ORD}=\$ 2,281.73\left[\dfrac{\left[(1+0.0245)^{\frac{2}{12}}\right]^{36}-1}{(1+0.0245)^{\frac{2}{12}}-1}\right]=\$ 88,228.30609 \nonumber \]
Balance:
\(\$ 404,821.7959-\$ 88,228.30609=\$ 316,593.49 \)
Step 6:
\( i=5.85 \% / 2=2.925 \% ; N=12 \times 17=204 \) payments
\[\$ 316,593.49=PMT\left[\dfrac{1-\left[\dfrac{1}{(1+0,02925)^{\frac{2}{12}}}\right]^{204}}{(1+0.02925)^{\frac{2}{12}}-1}\right] \nonumber \]
\[PMT=\dfrac{\$ 316,593.49}{\left [ \dfrac{1-\left [\dfrac{1}{(1+0.02925)^{\frac{2}{12}}}\right ]^{204}}{(1+0.02925)^{\frac{2}{12}}-1} \right ]}= \$ 2,440.73 \nonumber \]
Step 7:
\[\$ 2,440.73-\$ 2,281.73=\$ 159.00 \nonumber \]
| Action | Mode | N | I/Y | PV | PMT | FV | P/Y | C/Y |
|---|---|---|---|---|---|---|---|---|
| First Term Payment | END | 240 | 4.9 | 350100 | Answer: -2,281.730755 | 0 | 12 | 2 |
| Balance at end of First Term | \(\surd\) | 36 | c | \(\surd\) | -2,281.73 | Answer: -316,593.4898 | \(\surd\) | \(\surd\) |
| Second Term Payment | \(\surd\) | 204 | 5.85 | 316593.49 | Answer: -2,440.733592 | 0 | \(\surd\) | \(\surd\) |
The initial mortgage payment for the three-year term was $2,281.73. Upon renewal at the higher interest rate, the monthly payment increased by $159.00 to $2,440.73.
References
1 Canadian Real Estate Association (CREA), “Housing Market Stats”, https://www.crea.ca/housing-market-stats/ (accessed July 9, 2011).
2 Living In Canada, “Canadian House Prices,” www.livingin-canada.com/house-prices-canada.html (accessed July 9, 2011).
3 Statistics Canada, “Median Total Income, by Family Type, by Province and Territory, CANSIM table 111-0009, www40.statcan.ca/l01/cst01/famil108a-eng.htm (accessed October 19, 2010).