5.11: Linear Programming

Figure \(\PageIndex{1}\) : The aftermath of an earthquake and tsunami. (credit: modification of work "Earthquake and Tsunami Japan" by Climate and Ecosystems Change Adaptation Research University Network/Flickr, CC BY 2.0)

Learning Objectives

1. Compose an objective function to be minimized or maximized.
2. Compose inequalities representing a system application.
3. Apply linear programming to solve application problems.

Imagine you hear about some natural disaster striking a far-away country; it could be an earthquake, a fire, a tsunami, a tornado, a hurricane, or any other type of natural disaster. The survivors of this disaster need help—they especially need food, water, and medical supplies. You work for a company that has these supplies, and your company has decided to help by flying the needed supplies into the disaster area. They want to maximize the number of people they can help. However, there are practical constraints that need to be taken into consideration; the size of the airplanes, how much weight each airplane can carry, and so on. How do you solve this dilemma? This is where linear programming comes into play. Linear programming is a mathematical technique to solve problems involving finding maximums or minimums where a linear function is limited by various constraints.

As a field, linear programming began in the late 1930s and early 1940s. It was used by many countries during World War II; countries used linear programming to solve problems such as maximizing troop effectiveness, minimizing their own casualties, and maximizing the damage they could inflict upon the enemy. Later, businesses began to realize they could use the concept of linear programming to maximize output, minimize expenses, and so on. In short, linear programming is a method to solve problems that involve finding a maximum or minimum where a linear function is constrained by various factors.

Who Knew?: A Mathematician Invents a “Tsunami Cannon”

On December 26, 2004, a massive earthquake occurred in the Indian Ocean. This earthquake, which scientists estimate had a magnitude of 9.0 or 9.1 on the Richter Scale, set off a wave of tsunamis across the Indian Ocean. The waves of the tsunami averaged over 30 feet (10 meters) high, and caused massive damage and loss of life across the coastal regions bordering the Indian Ocean.

Usama Kadri works as an applied mathematician at Cardiff University in Wales. His areas of research include fluid dynamics and non-linear phenomena. Lately, he has been focusing his research on the early detection and easing of the effects of tsunamis. One of his theories involves deploying a series of devices along coastlines which would fire acoustic-gravity waves (AGWs) into an oncoming tsunami, which in theory would lessen the force of the tsunami. Of course, this is all in theory, but Kadri believes it will work. There are issues with creating such a device: they would take a tremendous amount of electricity to generate an AGW, for instance, but if it would save lives, it may well be worth it.

Compose an Objective Function to Be Minimized or Maximized

An objective function is a linear function in two or more variables that describes the quantity that needs to be maximized or minimized.

Example \(\PageIndex{1}\): Composing an Objective Function for Selling Two Products

Miriam starts her own business, where she knits and sells scarves and sweaters out of high-quality wool. She can make a profit of $8 per scarf and $10 per sweater. Write an objective function that describes her profit.

Answer

Let \(x\) represent the number of scarves sold, and let \(y\) represent the number of sweaters sold. Let \(P\) represent profit. Since each scarf has a profit of \(\$ 8\) and each sweater has a profit of \(\$ 10\), the objective function is \(P=8 x+10 y\).

Your Turn \(\PageIndex{1}\)

For a fundraiser at school, the Robotics Club is selling bags of apples and bunches of bananas during lunch. They will make a profit of $4 per bag of apples and $6 per bunch of bananas. Write an objective function that describes the profit the Robotics Club will make.

Example \(\PageIndex{2}\): Composing an Objective Function for Production

William’s factory produces two products, widgets and wadgets. It takes 24 minutes for his factory to make 1 widget, and 32 minutes for his factory to make 1 wadget. Write an objective function that describes the time it takes to make the products.

Answer

Let \(x\) equal the number of widgets made; let \(y\) equal the number of wadgets made; let \(T\) represent total time. The objective function is \(T=24 x+32 y\).

Your Turn \(\PageIndex{2}\)

Suppose William has a second factory that can make widgets in 20 minutes and wadgets in 28 minutes. Write an objective function that describes the time it takes to make the products.

Composing Inequalities Representing a System Application

For our two examples of profit and production, in an ideal world the profit a person makes and/or the number of products a company produces would have no restrictions. After all, who wouldn’t want to have an unrestricted profit? However in reality this is not the case; there are usually several variables that can restrict how much profit a person can make or how many products a company can produce. These restrictions are called constraints.

Many different variables can be constraints. When making or selling a product, the time available, the cost of manufacturing and the amount of raw materials are all constraints. In the opening scenario with the tsunami, the maximum weight on an airplane and the volume of cargo it can carry would be constraints. Constraints are expressed as linear inequalities; the list of constraints defined by the problem forms a system of linear inequalities that, along with the objective function, represent a system application.

Example \(\PageIndex{3}\): Representing the Constraints for Selling Two Products

Two friends start their own business, where they knit and sell scarves and sweaters out of high-quality wool. They can make a profit of $8 per scarf and $10 per sweater. To make a scarf, 3 bags of knitting wool are needed; to make a sweater, 4 bags of knitting wool are needed. The friends can only make 8 items per day, and can use not more than 27 bags of knitting wool per day. Write the inequalities that represent the constraints. Then summarize what has been described thus far by writing the objective function for profit and the two constraints.

Answer

Let \(x\) represent the number of scarves sold, and let \(y\) represent the number of sweaters sold. There are two constraints: the number of items the business can make in a day (a maximum of 8 ) and the number of bags of knitting wool they can use per day (a maximum of 27). The first constraint (total number of items in a day) is written as:

\[x+y \leq 8\]

Since each scarf takes 3 bags of knitting wool and each sweater takes 4 bags of knitting wool, the second constraint, total bags of knitting wool per day, is written as:

\[3 x+4 y \leq 27\]

In summary, here are the equations that represent the new business: \(P=8 x+10 y\); This is the profit equation: The business makes \(\$ 8\) per scarf and \(\$ 10\) per sweater.

\[\begin{aligned}
x+y & \leq 8 \\
3 x+4 y & \leq 27
\end{aligned}\]
 

Your Turn \(\PageIndex{3}\)

For a fudraiser at school, the Robotics Club is selling bags of apples and bunches of bananas during lunch. They will make a profit of $4 per bag of apples and $6 per bunch of bananas. Due to school health regulations, the club is allowed to have only 20 bags and bunches of fruit on school grounds each day to sell. Another regulation: the container where the Robotics Club keeps the fruit has a maximum weight capacity of 70 pounds. Each bag of apples weighs 3 pounds, while each bunch of bananas weighs 5 pounds. Write the inequalities that represent these constraints. Then summarize the equations that represent this system.

Example \(\PageIndex{4}\): Representing Constraints for Production

A factory produces two products, widgets and wadgets. It takes 24 minutes for the factory to make 1 widget, and 32 minutes for the factory to make 1 wadget. Research indicates that long-term demand for products from the factory will result in average sales of 12 widgets per day and 10 wadgets per day. Because of limitations on storage at the factory, no more than 20 widgets or 17 wadgets can be made each day. Write the inequalities that represent the constraints. Then summarize what has been described thus far by writing the objective function for time and the two constraints.

Answer

Let \(x\) equal the number of widgets made; let \(y\) equal the number of wadgets made. Based on the long-term demand, we know the factory must produce a minimum of 12 widgets and 10 wadgets per day. We also know because of storage limitations, the factory cannot produce more than 20 widgets per day or 17 wadgets per day. Writing those as inequalities, we have:

\[\begin{array}{l}
x \geq 12 \\
y \geq 10 \\
x \leq 20 \\
y \leq 17
\end{array}\]

The number of widgets made per day must be between 12 and 20 , and the number of wadgets made per day must be between 10 and 17. Therefore, we have:

\[\begin{array}{l}
12 \leq x \leq 20 \\
10 \leq y \leq 17
\end{array}\]

The system is:

\[\begin{array}{l}
T=24 x+32 y \\
12 \leq x \leq 20 \\
10 \leq y \leq 17
\end{array}\]

\(T\) is the variable for time; it takes 24 minutes to make a widget and 32 minutes to make a wadget.

Your Turn \(\PageIndex{4}\)

Suppose a second factory can make widgets in 20 minutes and wadgets in 28 minutes. Research for this factory indicates that long-term demand for products from this second factory will result in average sales of 15 widgets per day and 13 wadgets per day. Because of limitations on storage at his factory, no more than 22 widgets or 19 wadgets can be made each day. Write the inequalities that represent the constraints. Then summarize what has been described thus far by writing the objective function for time and the two constraints.

Applying Linear Programming to Solve Application Problems

There are four steps that need to be completed when solving a problem using linear programming. They are as follows:

Step 1: Compose an objective function to be minimized or maximized.

Step 2: Compose inequalities representing the constraints of the system.

Step 3: Graph the system of inequalities representing the constraints.

Step 4: Find the value of the objective function at each corner point of the graphed region.

The first two steps you have already learned. Let’s continue to use the same examples to illustrate Steps 3 and 4.

Example \(\PageIndex{5}\): Solving a Linear Programming Problem for Two Products

Three friends start their own business, where they knit and sell scarves and sweaters out of high-quality wool. They can make a profit of $8 per scarf and $10 per sweater. To make a scarf, 3 bags of knitting wool are needed; to make a sweater, 4 bags of knitting wool are needed. The friends can only make 8 items per day, and can use not more than 27 bags of knitting wool per day. Determine the number of scarves and sweaters they should make each day to maximize their profit.

Answer

Step 1: Compose an objective function to be minimized or maximized. From Example 5.98, the objective function is \(P=8 x+10 y\).
 

Step 2: Compose inequalities representing the constraints of the system. From Example 5.98, the constraints are \(x+y \leq 8\) and \(3 x+4 y \leq 27\).
 

Step 3: Graph the system of inequalities representing the constraints. Using methods discussed in Graphing Linear Equations and Inequalities, the graphs of the constraints are shown below. Because the number of scarves \((x)\) and the number of sweaters \((y)\) both must be non-negative numbers (i.e., \(x \geq 0\) and \(y \geq 0\) ), we need to graph the system of inequalities in Quadrant I only. Figure \(\PageIndex{2}\) shows each constraint graphed on its own axes, while Figure \(\PageIndex{3}\) shows the graph of the system of inequalities (the two constraints graphed together). In Figure \(\PageIndex{4}\) , the large shaded region represents the area where the two constraints intersect. If you are unsure how to graph these regions, refer back to Graphing Linear Equations and Inequalities.

Figure 5. \(\PageIndex{2}\) Graphs of each constraint

Figure \(\PageIndex{3}\) : Graph of the System of Inequalities

Step 4: Find the value of the objective function at each corner point of the graphed region. The “graphed region” is the area where both of the regions intersect; in Figure 5.112, it is the large shaded area. The “corner points” refer to each vertex of the shaded area. Why the corner points? Because the maximum and minimum of every objective function will occur at one (or more) of the corner points. Figure 5.112 shows the location and coordinates of each corner point.

Figure \(\PageIndex{4}\) : Graph of Region with Corner Points

Three of the four points are readily found, as we used them to graph the regions; the fourth point, the intersection point of the two constraint lines, will have to be found using methods discussed in Systems of Linear Equations in Two Variables, either using substitution or elimination. As a reminder, set up the two equations of the constraint lines:

\[\begin{aligned}
3 x+4 y & =27 \\
x+y & =8
\end{aligned}\]

For this example, substitution will be used.

\[\begin{aligned}
x+y & =8 \\
y & =8-x .
\end{aligned}\]

Substituting \(8-x\) into the first equation for \(y\), we have

\[\begin{aligned}
3 x+4(8-x) & =27 \\
3 x+32-4 x & =27 \\
-x & =-5 \\
x & =5
\end{aligned}\]

Now, substituting the 5 in for \(x\) in either equation to solve for \(y\). Choosing the second equation, we have:

\[\begin{array}{r}
5+y=8 \\
y=3
\end{array}\]

Therefore, \(x=5\), and \(y=3\).

To find the value of the objective function, \(P=8 x+10 y\), put the coordinates for each corner point into the equation and solve. The largest solution found when doing this will be the maximum value, and thus will be the answer to the question originally posed: determining the number of scarves and sweaters the new business should make each day to maximize their profit.

Corner \((x, y)\)	Objective Function \(P=8 x+10 y\)
\((0,0)\)	\(P=8(0)+10(0)=0\)
\((0,6.75)\)	\(P=8(0)+10(6.75)=40+30 = 70\)
\((5,3)\)	\(P=8(5)+10(3)=67.5\)
\((8,0)\)	\(P=8(8)+10(0)=64\)

The maximum value for the profit \(P\) occurs when \(x=5\) and \(y=3\). This means that to maximize their profit, the new business should make 5 scarves and 3 sweaters every day.

 

Your Turn \(\PageIndex{5}\)

For a fundraiser at school, the Robotics Club is selling bags of apples and bunches of bananas during lunch. They will make a profit of $4 per bag of apples and $6 per bunch of bananas. Due to school health regulations, the club is allowed to have only 20 bags and bunches of fruit on school grounds each day to sell. Another regulation: the container where the Robotics Club keeps the fruit has a maximum weight capacity of 70 pounds. Each bag of apples weighs 3 pounds, while each bunch of bananas weighs 5 pounds. Determine the number of bags of apples and the number of bags of bananas the Robotics Club should sell each day to maximize their profit.

 

People in Mathematics: Leonid Kantorovich

Leonid Vitalyevich Kantorovich was born January 19, 1912, in St. Petersburg, Russia. Two major events affected young Leonid’s life: when he was five, the Russian Revolution began, making life in St. Petersburg very difficult; so much so that Leonid’s family fled to Belarus for a year. When Leonid was 10, his father died, leaving his mother to raise five children on her own.

Despite the hardships, Leonid showed incredible mathematical ability at a young age. When he was only 14, he enrolled in Leningrad State University to study mathematics. Four years later, at age 18, he graduated with what would be equivalent to a Ph.D. in mathematics.

Although his primary interests were in pure mathematics, in 1938 he began working on problems in economics. Supposedly, he was approached by a local plywood manufacturer with the following question: how to come up with a work schedule for eight lathes to maximize output, given the five different kinds of plywood they had at the factory. By July 1939, Leonid had come up with a solution, not only to the lathe scheduling problem but to other areas as well, such as an optimal crop rotation schedule for farmers, minimizing waste material in manufacturing, and finding optimal routes for transporting goods. The technique he discovered to solve these problems eventually became known as linear programming. He continued to use this technique for solving many other problems involving optimization, which resulted in the book The Best Use of Economic Resources, which was published in 1959. His continued work in linear programming would ultimately result in him winning the Nobel Prize of Economics in 1975.

Check Your Understanding

 

1. Kellie makes tables and chairs. Kellie profits $20 from a table (\(t\)), and $10 from a chair (\(c\)). The objective function for profit in this situation is:

1. \({P = 20t - 10c}\)
2. \({P = 20c + 10t}\)
3. \({P = 20t + 10c}\)
4. \({P = 20c - 10t}\)

 

2. Dave grows wheat (\(w\)) and barley (\(b\)) on a farm. Dave expects to profit $150 per acre for wheat and $180 per acre for barley. The objective function for profit in this situation is:

1. \({P = 150w + 180b}\)
2. \({P = 150b + 180w}\)
3. \({P = 180w + 150b}\)
4. \({P = 150w - 180b}\)

 

3. An antique music store sells two types of vinyl records; 45 rpm records (\(f\)) and 33 rpm records (\(t\)). It makes a profit of $2.50 for each 45 rpm record and $6.75 for each 33 rpm record. The objective function for profit in this situation is:

1. \({P = 2.50f + 6.75c}\)
2. \({P = 2.50f + 6.75t}\)
3. \({P = 2.50t + 6.75f}\)
4. None of these

 

4. Kellie makes tables and chairs. Kellie profits $20 from a table (\(t\)), and $10 from a chair (\(c\)). A table requires 15 board feet of wood, while a chair requires 4 board feet of wood. Kellie has 70 board feet available. What is the constraint inequality in this situation?

1. \({20t + 10c \leq 70}\)
2. \({ t + c \leq 70}\)
3. \({ 15t + 4c \geq 70}\)
4. \({ 15t + 4c \leq 70}\)

 

5. Kellie makes tables and chairs. Kellie profits $20 from a table (\(t\)), and $10 from a chair (\(c\)). The maximum number of tables and chairs Kellie can make in any one day is 12. What is the constraint inequality in this situation?

1. \({t + c \leq 12}\)
2. \({ 20t + 10c \leq 12}\)
3. \({ 20t + 10c \geq 12}\)
4. \({ 20t + 10c \leq 70}\)

 

6. Dave grows wheat (\(w\)) and barley (\(b\)) on a farm. Dave expects to profit $150 per acre for wheat and $180 per acre for barley. The cost of seed is $10 per acre for wheat and $15 per acre for barley. Dave can only afford to spend $945 on seed. What is the constraint inequality in this situation?

1. \({w + b \leq 945}\)
2. \({ 10w + 15b \geq 945}\)
3. \({ 10w + 15b \leq 945}\)
4. \({ 150w + 180w \leq 945}\)

 

7. Dave grows wheat (\(w\)) and barley (\(b\)) on a farm. Dave expects to profit $150 per acre for wheat and $180 per acre for barley. The cost of raising each crop is $30 per acre for wheat and $25 per acre for barley. Dave budgets $1,635 for the raising of both crops. What is the constraint inequality in this situation?

1. \({150w + 180b \leq \text{1,635}}\)
2. \({25w + 30b \leq \text{1,635}}\)
3. \({w + b \leq \text{1,635}}\)
4. \({30w + 25b \leq \text{1,635}}\)

 

8. Kellie makes tables and chairs. Kellie profits $20 from a table (\(t\)), and $10 from a chair (\(c\)). A table requires 15 board feet of wood, while a chair requires 4 board feet of wood. Kellie has 70 board feet available. The maximum number of tables and chairs Kellie can make in any one day is 12. The graph of the system of inequalities representing the constraints is:

 

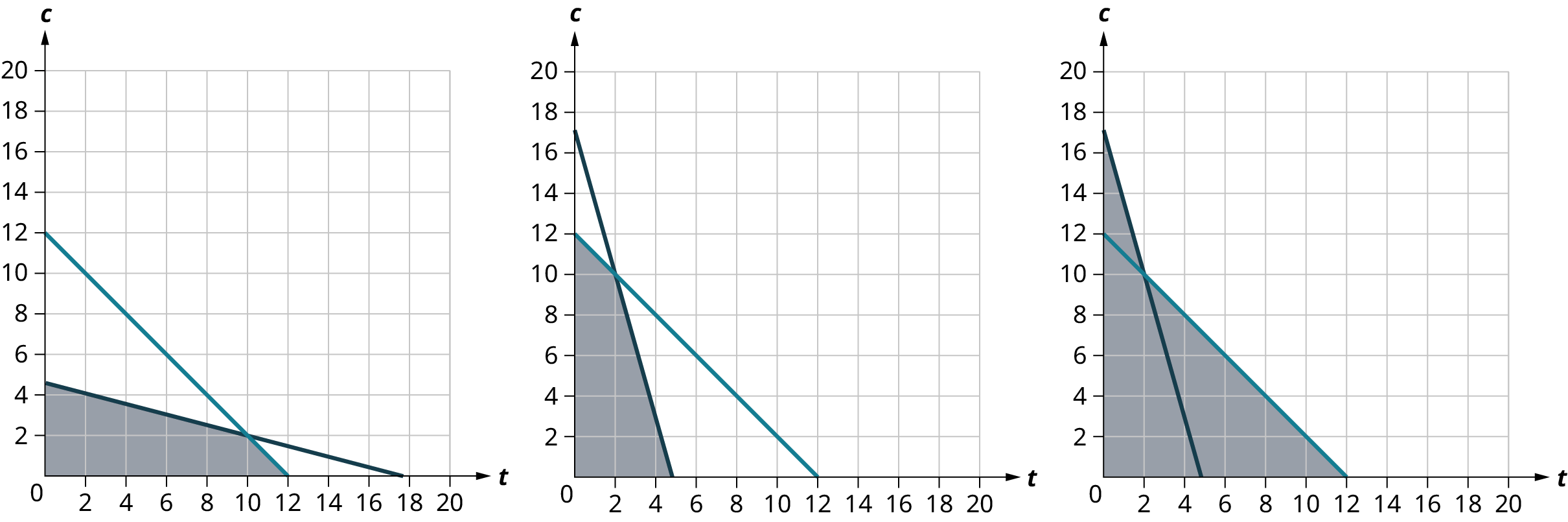
9. Kellie makes tables and chairs. Kellie profits $20 from a table (\(t\)), and $10 from a chair (\(c\)). A table requires 15 board feet of wood, while a chair requires 4 board feet of wood. Kellie has 70 board feet available. The maximum number of tables and chairs Kellie can make in any one day is 12. The four corner points of the system are:

1. \({(0, 0), (0, 12), (10, 2), (12, 0)}\)
2. \({(0, 0), (0, 12), (2, 10), (4\tfrac{2}{3} , 0)}\)
3. \({(0, 0), (17.5, 0), (2, 10), (12, 0)}\)

 

10. Kellie makes tables and chairs. Kellie profits $20 from a table (\(t\)), and $10 from a chair (\(c\)). A table requires 15 board feet of wood, while a chair requires 4 board feet of wood. Kellie has 70 board feet available. The maximum number of tables and chairs Kellie can make in any one day is 12. The maximum profit Kellie can make in one day is:
\($220\quad\quad{$120}\quad\quad{$140}\quad\quad{$24}\)