5.11.1: Exercises
- Page ID
- 169548
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
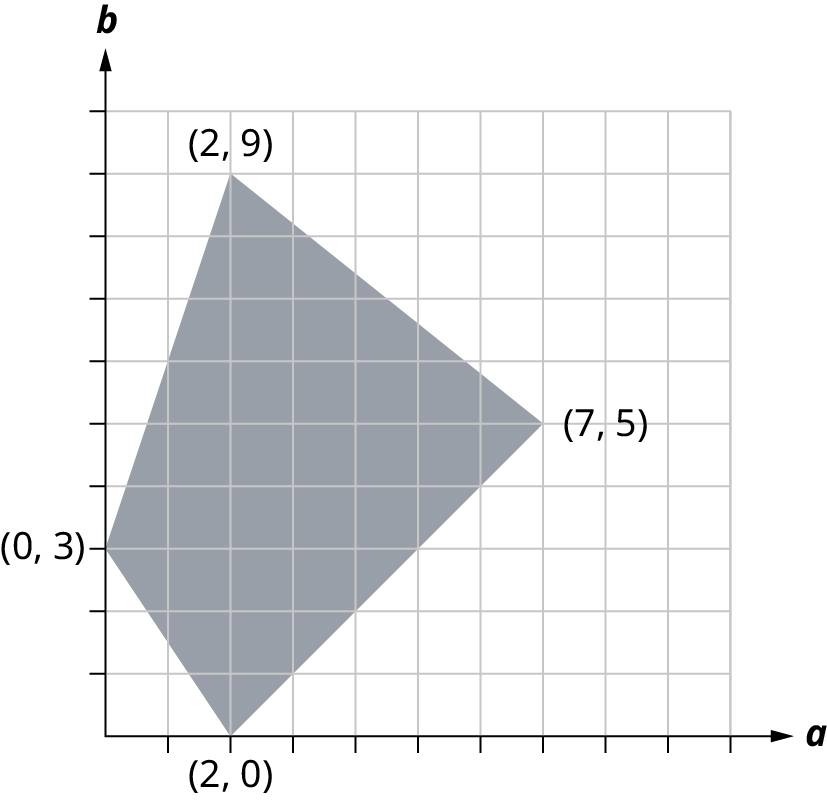
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)For the following exercises, find the value of the objective function at each corner of the graphed region.
Objective Function \(P = 6x + 11y\).
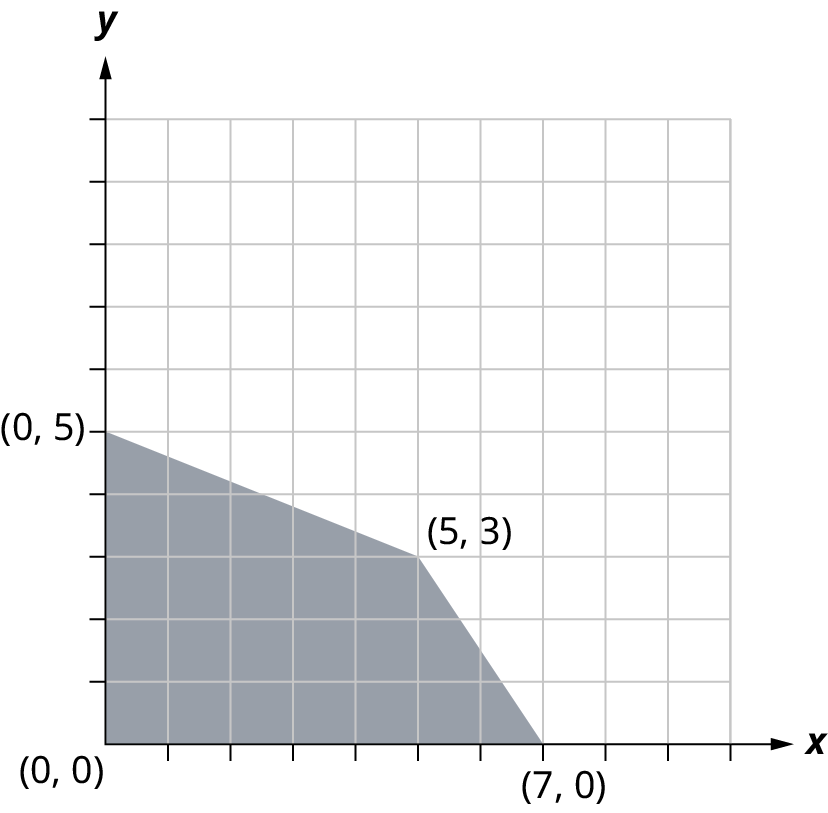
Objective Function \(T = 5x + 3y\)
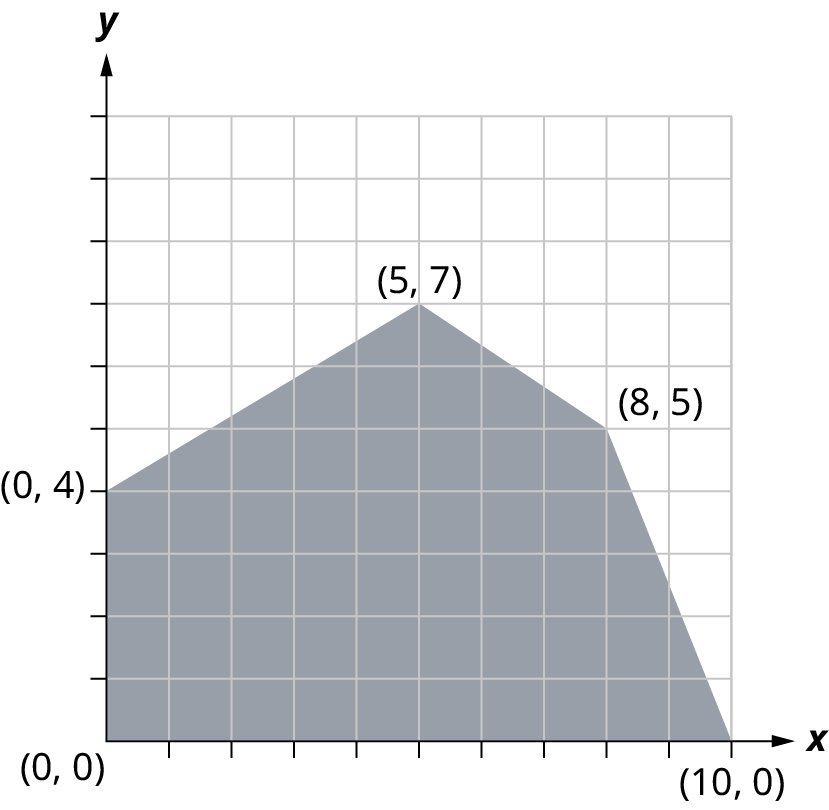
Objective Function \(L = 33x + 45y\)
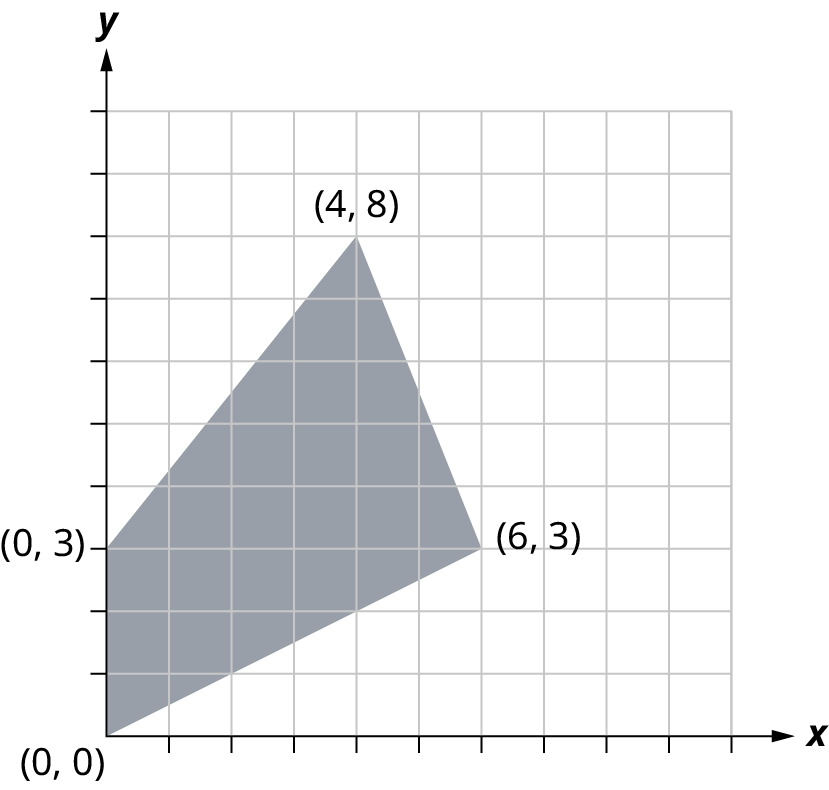
Objective Function \(P = 2t + 4c\)
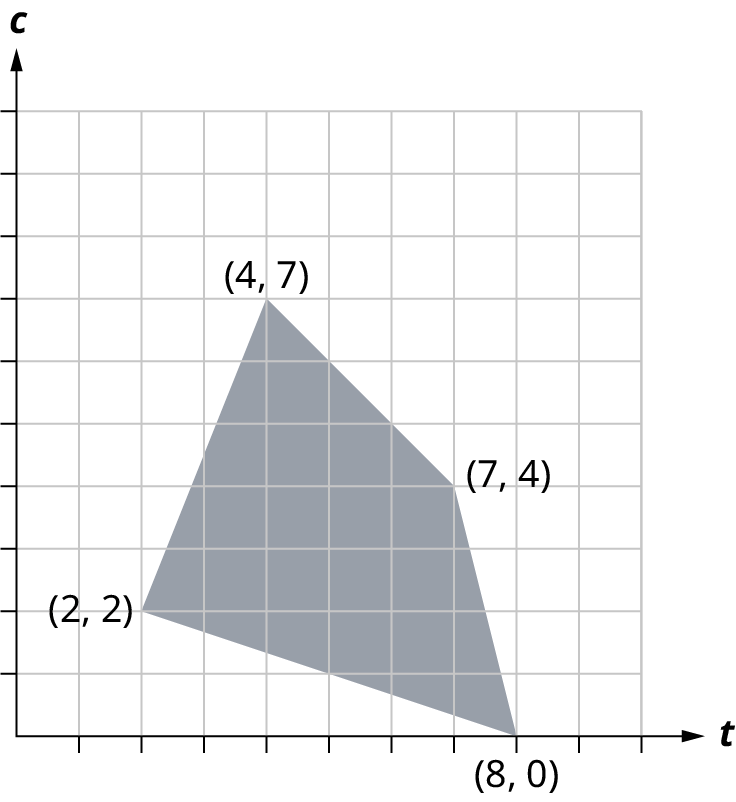
Objective Function \(P = 2.5a + 3.75b\)
For the following exercises, write the constraint inequalities. The variables to use are given in parentheses.
Fernando builds birdbaths \((x)\) and birdhouses \((y)\). Fernando can make a total of 7 birdbaths and birdhouses per day. A birdbath costs $8 to make, while a birdhouse costs $6 to make. Fernando has $48 to spend on building materials for the day. When he sells them, Fernando makes $12 in profit on a birdbath and $9 in profit on a birdhouse.
A fruit pie \((p)\) requires 12 ounces of fruit and 15 ounces of dough; a fruit tart \((t)\) requires 4 ounces of fruit and 3 ounces of dough. There are 72 ounces of fruit and 60 ounces of dough.
One recipe for chocolate cake \((c)\) calls for 9 ounces of chocolate chips and 4 eggs; a recipe for dark chocolate cake \((d)\) requires 12 ounces of chocolate chips but only 3 eggs. There are 90 ounces of chocolate chips and 36 eggs.
To build an outdoor bench \((b)\), a carpenter needs 10 pieces of wood and 26 nails; to build an outdoor chair \((c)\), the carpenter need 8 pieces of wood and 33 nails. There are 92 pieces of wood and 286 nails.
For the following exercises, graph each of the system of inequalities from Exercises 6–9. Assume all graphs are in the first quadrant.
Graph of Exercise 6
Graph of Exercise 7
Graph of Exercise 8
Graph of Exercise 9
For the following exercises, use the four steps for solving linear programming problems to solve.
A restaurant sells both regular milk and chocolate milk. To make a glass of regular milk (\(x\)), it takes 16 ounces of, well, milk. To make a glass of chocolate milk (\(y\)), it takes 15 ounces of milk and 1 ounce of chocolate flavoring. The restaurant makes a profit of $1.50 per glass on regular milk and $1.00 per glass on chocolate milk. At the beginning of the day, the restaurant has 600 ounces of milk and 24 ounces of chocolate flavoring. To maximize profits, how much of each should they sell that day?
To make a package of all-beef hot dogs (\(x\)), a factory uses one pound of beef; to make their regular all-meat hot dogs (\(y\)), they use ½ pound of beef and ½ pound of pork. The profit on the package of all-beef hot dogs is $2.40 per pack; the profit on the all-meat hot dogs is $3.20 per pack. If there are 400 pounds of beef and 250 pounds of pork available, how many of each product should the factory make to maximize their profit?
A toy maker makes two plastic toys, the Ring (\(x\)) and the Stick (\(y\)). The toy maker makes $5 per Ring and $4 per Stick. The Ring uses 4 feet of plastic, while the Stick uses 3 feet of plastic. Today the toy maker has 36 feet of plastic available. The toy maker also only makes 10 plastic toys per day. To maximize profit, how many of each toy should the toy maker make?
The toy maker also makes exactly two toys out of wood, the Box (\(x\)) and the Bat (\(y\)). The toy maker makes $6 per Box and $7 per Bat. Each Box requires 25 ounces of wood, and each Bat requires 40 ounces of wood. Today the toy maker has 260 ounces of wood available. The toy maker also only makes 8 wooden toys per day. To maximize profit, how many of each wooden toy should the toy maker make?
Sara makes two kinds of kites out of fabric and popsicle sticks. Her Famous Flyer (\(x\)) needs 2 yards of fabric and 9 popsicle sticks; her Gallant Glider (\(y\)) needs 3 yards of fabric and 18 popsicle sticks. She makes a profit of $4 on the Famous Flyer and $6 on the Gallant Glider. Today she has 30 yards of fabric and 153 popsicle sticks. How many of each kite should she make to maximize her profit?
Randy’s RV Storage stores two types of Recreational Vehicles (RVs), The Xtra RV (\(x\)) takes up 400 square feet of space, while the Yosemite RV (\(y\)) takes up 600 square feet of space. Randy has 55,000 square feet of storage space. By local law, he is only allowed to have a maximum of 100 RVs on his property at any one time. He charges $60 a month to store an Xtra RV, and $80 a month to store a Yosemite RV. How many of each should he store in order to maximize his profit?
A Belgian chocolatier wants to introduce two new chocolate bar creations. The first chocolate bar is called Super Dark (\(x\)), and it consists of 90 grams of chocolate and 10 grams of sugar. The second chocolate bar is called Special Dark (\(y\)), containing 80 grams of chocolate and 20 grams of sugar. She calculates that her company will make 1 Euro per bar of Super Dark, and 2 Euros per bar on Special Dark. She first will create some samples to sell out of 1,260 grams of chocolate and 240 grams of sugar. How many of each bar should the chocolatier create to maximize profit?
A juice bottler makes two kinds of specialty juices using different mixtures of pineapple (\(x\)) and orange (\(y\)) juices. A 16-ounce bottle of Island Delight has 10 ounces of pineapple juice and 6 ounces of orange juice. A 16-ounce bottle of Sun Fun has 4 ounces of pineapple juice and 12 ounces of orange juice. The bottler makes $1.60 per bottle on Island Delight and $1.20 per bottle on Sun Fun. The amounts of juice available today are 640 ounces of pineapple juice and 768 ounces of orange juice. To maximize profit, how many of each bottle of juice should the juice bottler make?
Fernando builds birdbaths (\(x\)) and birdhouses (\(y\)). Fernando can make a total of 7 birdbaths and birdhouses per day. A birdbath costs $8 to make, while a birdhouse costs $6 to make. Fernando has $48 to spend on building materials for the day. When he sells them, Fernando makes $12 in profit on a birdbath and $9 in profit on a birdhouse. Determine how many of each Fernando should make to maximize his profit for the day.
A farmer grows wheat (\(x\)) and barley (\(y\)) on his 500 acres of cropland. He expects to profit $150 per acre for wheat and $180 per acre for barley. The cost of raising each crop (seed, pesticide, etc.) is $60 per acre for wheat and $90 per acre for barley. The farmer can budget $36,000 for the growing of the crops. To maximize his profit, how many acres of each crop should be grown?
A company is going to ship food (\(x\)) and water (\(y\)) to the victims of a tsunami. Each container of food will feed 8 people for a day, and each container of water will give 12 people their daily water. The food containers each weigh 30 pounds and take up 8 cubic feet of space; each container of water weighs 120 pounds, but takes up only 2 cubic feet of space. The airplanes lined up to carry the supplies to the victims cannot have its cargo exceed 24,000 pounds; also, the total cargo area in the airplanes is 4,000 cubic feet. How many containers of food and water can be sent with each plane shipment that maximizes the shipment?
Another company will send clothing (\(x\)) and medical supplies (\(y\)) to the victims of the tsunami. Each container of clothing contains enough clothing for 12 people; each container of medical supplies can aid 8 people. The clothing containers each weigh 50 pounds and take up 6 cubic feet of space; each container of medical supplies weighs 20 pounds, and takes up 4 cubic feet of space. The airplanes lined up to carry the supplies to the victims cannot have its cargo exceed 24,000 pounds; also, the total cargo area in the airplanes is 3,000 cubic feet. How many containers of clothing and medical supplies can be sent with each plane shipment that maximizes the shipment?

