4.4: Arguments
- Page ID
- 59947
A logical argument is a claim that a set of premises support a conclusion. There are two general types of arguments: inductive and deductive arguments.
An inductive argument uses a collection of specific examples as its premises and uses them to propose a general conclusion.
A deductive argument uses a collection of general statements as its premises and uses them to propose a specific situation as the conclusion.
The argument “when I went to the store last week I forgot my purse, and when I went today I forgot my purse. I always forget my purse when I go the store” is an inductive argument.
Solution
The premises are:
- I forgot my purse last week
- I forgot my purse today
The conclusion is:
- I always forget my purse
Notice that the premises are specific situations, while the conclusion is a general statement. In this case, this is a fairly weak argument, since it is based on only two instances.
The argument “every day for the past year, a plane flies over my house at 2 p.m. A plane will fly over my house every day at 2 p.m.” is a stronger inductive argument, since it is based on a larger set of evidence.
An inductive argument is never able to prove the conclusion true, but it can provide either weak or strong evidence to suggest it may be true.
Many scientific theories, such as the big bang theory, can never be proven. Instead, they are inductive arguments supported by a wide variety of evidence. Usually in science, an idea is considered a hypothesis until it has been well tested, at which point it graduates to being considered a theory. The commonly known scientific theories, like Newton’s theory of gravity, have all stood up to years of testing and evidence, though sometimes they need to be adjusted based on new evidence. For gravity, this happened when Einstein proposed the theory of general relativity.
A deductive argument is more clearly valid or not, which makes them easier to evaluate.
A deductive argument is considered valid if all the premises are true, and the conclusion follows logically from those premises. In other words, the premises are true, and the conclusion follows necessarily from those premises.
The argument “All cats are mammals and a tiger is a cat, so a tiger is a mammal” is a valid deductive argument.
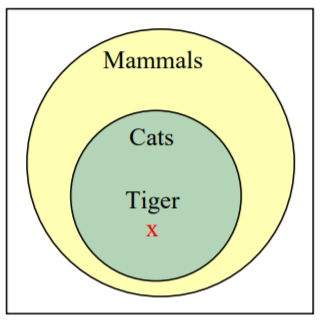The premises are:
- All cats are mammals
- A tiger is a cat
The conclusion is:
- A tiger is a mammal
Both the premises are true. To see that the premises must logically lead to the conclusion, one approach would be to use a Venn diagram. From the first premise, we can conclude that the set of cats is a subset of the set of mammals. From the second premise, we are told that a tiger lies within the set of cats. From that, we can see in the Venn diagram that the tiger also lies inside the set of mammals, so the conclusion is valid.
To analyze an argument with a Venn diagram
- Draw a Venn diagram based on the premises of the argument
- If the premises are insufficient to determine what determine the location of an element, indicate that.
- The argument is valid if it is clear that the conclusion must be true
Premise: All firefighters know CPR
Premise: Jill knows CPR
Conclusion: Jill is a firefighter
Solution
From the first premise, we know that firefighters all lie inside the set of those who know CPR. From the second premise, we know that Jill is a member of that larger set, but we do not have enough information to know if she also is a member of the smaller subset that is firefighters.
Since the conclusion does not necessarily follow from the premises, this is an invalid argument, regardless of whether Jill actually is a firefighter.
It is important to note that whether or not Jill is actually a firefighter is not important in evaluating the validity of the argument; we are only concerned with whether the premises are enough to prove the conclusion.
Determine the validity of this argument:
Premise: No cows are purple
Premise: Fido is not a cow
Conclusion: Fido is purple
In addition to these categorical style premises of the form “all ___”, “some ____”, and “no ____”, it is also common to see premises that are implications.
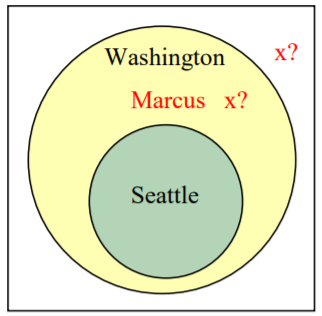Premise: If you live in Seattle, you live in Washington.
Premise: Marcus does not live in Seattle
Conclusion: Marcus does not live in Washington
Solution
From the first premise, we know that the set of people who live in Seattle is inside the set of those who live in Washington. From the second premise, we know that Marcus does not lie in the Seattle set, but we have insufficient information to know whether or not Marcus lives in Washington or not. This is an invalid argument.
Consider the argument “You are a married man, so you must have a wife.”
Solution
This is an invalid argument, since there are, at least in parts of the world, men who are married to other men, so the premise not insufficient to imply the conclusion.
Some arguments are better analyzed using truth tables.
Consider the argument
Premise: If you bought bread, then you went to the store
Premise: You bought bread
Conclusion: You went to the store
While this example is hopefully fairly obviously a valid argument, we can analyze it using a truth table by representing each of the premises symbolically. We can then look at the implication that the premises together imply the conclusion. If the truth table is a tautology (always true), then the argument is valid.
We’ll get \(B\) represent “you bought bread” and \(S\) represent “you went to the store”. Then the argument becomes:
Premise: \(B → S\)
Premise: \(B\)
Conclusion: \(S\)
To test the validity, we look at whether the combination of both premises implies the conclusion; is it true that \(\left[ (B→S) ⋀ B \right] → S\)?
| B | S | B→S | (B→S) ⋀ B | [(B→S) ⋀ B] → S | |||
| T | T | T | T | T | |||
| T | F | F | F | T | |||
| F | T | T | F | T | |||
| F | F | T | F | T | |||
Since the truth table for \(\left[ (B→S) ⋀ B \right] → S\) is always true, this is a valid argument.
Determine if the argument is valid:
Premise: If I have a shovel I can dig a hole.
Premise: I dug a hole
Conclusion: Therefore, I had a shovel
To analyze an argument with a truth table:
- Represent each of the premises symbolically
- Create a conditional statement, joining all the premises with and to form the antecedent, and using the conclusion as the consequent.
- Create a truth table for that statement. If it is always true, then the argument is valid.
Premise: If I go to the mall, then I’ll buy new jeans
Premise: If I buy new jeans, I’ll buy a shirt to go with it
Conclusion: If I got to the mall, I’ll buy a shirt.
Solution
Let \(M\) = I go to the mall, \(J\) = I buy jeans, and \(S\) = I buy a shirt.
The premises and conclusion can be stated as:
Premise: M → J
Premise: J → S
Conclusion: M → S
We can construct a truth table for \([(M→J) ⋀ (J→S)] → (M→S)\)
| M | J | S | M→J | J→S | (M→J) ⋀ (J→S) | M→S | [(M→J) ⋀ (J→S)] → (M→S) | |||
| T | T | T | T | T | T | T | T | |||
| T | T | F | T | F | F | F | T | |||
| T | F | T | F | T | F | T | T | |||
| T | F | F | F | T | F | F | T | |||
| F | T | T | T | T | T | T | T | |||
| F | T | F | T | F | F | T | T | |||
| F | F | T | T | T | T | T | T | |||
| F | F | F | T | T | T | T | T | |||
From the truth table, we can see this is a valid argument.
The previous problem is an example of a syllogism.
A syllogism is an implication derived from two others, where the consequence of one is the antecedent to the other. The general form of a syllogism is:
Premise: p → q
Premise: q → r
Conclusion: p → r
This is sometimes called the transitive property for implication.
Premise: If I work hard, I’ll get a raise.
Premise: If I get a raise, I’ll buy a boat.
Conclusion: If I don’t buy a boat, I must not have worked hard.
Solution
If we let W = working hard, R = getting a raise, and B = buying a boat, then we can represent our argument symbolically:
Premise: H → R
Premise: R → B
Conclusion: ~B → ~H
We could construct a truth table for this argument, but instead, we will use the notation of the contrapositive we learned earlier to note that the implication ~B → ~H is equivalent to the implication H → B. Rewritten, we can see that this conclusion is indeed a logical syllogism derived from the premises.
Is this argument valid?
Premise: If I go to the party, I’ll be really tired tomorrow.
Premise: If I go to the party, I’ll get to see friends.
Conclusion: If I don’t see friends, I won’t be tired tomorrow.
Lewis Carroll, author of Alice in Wonderland, was a math and logic teacher, and wrote two books on logic. In them, he would propose premises as a puzzle, to be connected using syllogisms.
Solve the puzzle. In other words, find a logical conclusion from these premises.
- All babies are illogical.
- Nobody is despised who can manage a crocodile.
- Illogical persons are despised
Solution
Let B = is a baby, D = is despised, I = is illogical, and M = can manage a crocodile.
Then we can write the premises as:
B → I
M → ~D
I → D
From the first and third premises, we can conclude that B → D; that babies are despised. Using the contrapositive of the second premised, D → ~M, we can conclude that B → ~M; that babies cannot manage crocodiles.
While silly, this is a logical conclusion from the given premises.