7.5: Exercises

Last updated
Save as PDF

Page ID: 34215

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Skills

Create a digraph for the following set of tasks:

$\begin{array}{|l|l|l|}
\hline \text { Task } & \text { Time required } & \begin{array}{l}
\text { Tasks that must be } \\
\text { completed first }
\end{array} \\
\hline \mathrm{A} & 3 & \\
\hline \mathrm{B} & 4 & \\
\hline \mathrm{C} & 7 & \\
\hline \mathrm{D} & 6 & \mathrm{A}, \mathrm{B} \\
\hline \mathrm{E} & 5 & \mathrm{B} \\
\hline \mathrm{F} & 5 & \mathrm{D}, \mathrm{E} \\
\hline \mathrm{G} & 4 & \mathrm{E} \\
\hline
\end{array}$

Create a digraph for the following set of tasks:

$\begin{array}{|l|l|l|}
\hline \text { Task } & \text { Time required } & \begin{array}{l}
\text { Tasks that must be } \\
\text { completed first }
\end{array} \\
\hline \mathrm{A} & 3 & \\
\hline \mathrm{B} & 4 & \\
\hline \mathrm{C} & 7 & \\
\hline \mathrm{D} & 6 & \mathrm{A} \\
\hline \mathrm{E} & 5 & \mathrm{A} \\
\hline \mathrm{F} & 5 & \mathrm{B} \\
\hline \mathrm{G} & 4 & \mathrm{D}, \mathrm{E} \\
\hline
\end{array}$

Use this digraph for the next 2 problems.

$sc17.svg$

Using the priority list $\mathrm{T}_{4}, \mathrm{T}_{1}, \mathrm{T}_{7}, \mathrm{T}_{3}, \mathrm{T}_{6}, \mathrm{T}_{2}, \mathrm{T}_{5}$, schedule the project with two processors.
Using the priority list $\mathrm{T}_{5}, \mathrm{T}_{2}, \mathrm{T}_{3}, \mathrm{T}_{7}, \mathrm{T}_{1}, \mathrm{T}_{4}, \mathrm{T}_{6}$, schedule the project with two processors.

Use this digraph for the next 4 problems.

$sc18.svg$

Using the priority list $\mathrm{T}_{4}, \mathrm{T}_{3}, \mathrm{T}_{9}, \mathrm{T}_{10}, \mathrm{T}_{8}, \mathrm{T}_{5}, \mathrm{T}_{6}, \mathrm{T}_{1}, \mathrm{T}_{7}, \mathrm{T}_{2}$ schedule the project with two processors.
Using the priority list $\mathrm{T}_{2}, \mathrm{T}_{4}, \mathrm{T}_{6}, \mathrm{T}_{8}, \mathrm{T}_{10}, \mathrm{T}_{1}, \mathrm{T}_{3}, \mathrm{T}_{5}, \mathrm{T}_{7}, \mathrm{T}_{9}$ schedule the project with two processors.
Using the priority list $\mathrm{T}_{4}, \mathrm{T}_{3}, \mathrm{T}_{9}, \mathrm{T}_{10}, \mathrm{T}_{8}, \mathrm{T}_{5}, \mathrm{T}_{6}, \mathrm{T}_{1}, \mathrm{T}_{7}, \mathrm{T}_{2}$ schedule the project with three processors.
Using the priority list $\mathrm{T}_{2}, \mathrm{T}_{4}, \mathrm{T}_{6}, \mathrm{T}_{8}, \mathrm{T}_{10}, \mathrm{T}_{1}, \mathrm{T}_{3}, \mathrm{T}_{5}, \mathrm{T}_{7}, \mathrm{T}_{9}$ schedule the project with three processors.

Use the decreasing time algorithm to create a priority list for the digraph from #3, and schedule with two processors.

Use the decreasing time algorithm to create a priority list for the digraph from #3, and schedule with three processors.

Use the decreasing time algorithm to create a priority list for the digraph from #5, and schedule with two processors.

Use the decreasing time algorithm to create a priority list for the digraph from #5, and schedule with three processors.

Use the decreasing time algorithm to create a priority list for the problem from #1, and schedule with two processors.

Use the decreasing time algorithm to create a priority list for the problem from #2, and schedule with two processors.

With the digraph from #3:

a. Apply the backflow algorithm to find the critical time for each task

b. Find the critical path for the project and the minimum completion time

c. Use the critical path algorithm to create a priority list and schedule on two processors.

With the digraph from #3, use the critical path algorithm to schedule on three processors.

With the digraph from #5:

a. Apply the backflow algorithm to find the critical time for each task

b. Find the critical path for the project and the minimum completion time

c. Use the critical path algorithm to create a priority list and schedule on two processors.

With the digraph from #5, use the critical path algorithm to schedule on three processors.

Use the critical path algorithm to schedule the problem from #1 on two processors.

Use the critical path algorithm to schedule the problem from #2 on two processors.

Concepts

If an additional order requirement is added to a digraph, can the optimal finishing time ever become longer? Can the optimal finishing time ever become shorter?

Will an optimal schedule always have no idle time?

Consider the digraph below.

$sc19.svg$

How many priority lists could be created for these tasks?
How many unique schedules are created by those priority lists?

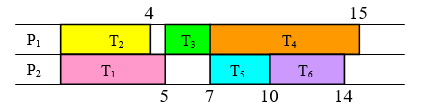
Create a digraph and priority list that would lead to the schedule below.

$clipboard_ef0cf2d2798287b75ab51f13c0cd0dd90.png$

Is it possible to create a digraph with three tasks for which every possible priority list creates a different schedule? If so, create it.

Is it possible to create a digraph with four tasks for which every possible priority list creates a different schedule? If so, create it.

Exploration

Independent tasks are ones that have no order requirements; they can be completed in any order.

a. Consider three tasks, with completion times 2, 2, and 4 hours respectively. Construct two different schedules on two processors with different completion times to show that the priority list still matters with independent tasks.

b. Choose a set of independent tasks with different completion times, and implement the decreasing time list algorithm and the critical path algorithm. What do you observe?

c. Will using the decreasing time list or critical path algorithms with independent tasks always produce an optimal schedule? Why or why not?

d. Will using the decreasing time list or critical path algorithms with independent tasks always produce the same schedule? Why or why not?

In a group, choose ten tasks necessary to throw a birthday party for a friend or child (for example, cleaning the house or buying a cake). Determine order requirements for the tasks, create a digraph, and schedule the tasks for two people.

29-37: At the end of the chapter it was noted that no algorithm exists to determine if an arbitrary schedule is optimal, but there are special cases where we can determine that a schedule is indeed optimal. In each of the following scenarios, determine

If the scenario is even possible
Whether or not the schedule could be optimal
Whether or not we can be sure that the schedule is optimal

A job has a critical time of 30 hours, and the finishing time for the schedule on 2 processors is 30 hours.
The sum of all task times for a job is 40 hours, and the finishing time for the schedule on 2 processors was 15 hours
The sum of all task times for a job is 100 hours, the critical time of the job was 40 hours, and the finishing time for the schedule on 2 processors was 50 hours.
The sum of all task times for a job is 50 hours, and the finishing time for the schedule on 2 processors was 40 hours.
A job has a critical time of 30 hours, and the finishing time for the schedule on 3 processors is 20 hours.
The sum of all task times for a job is 60 hours, and the finishing time for the schedule on 3 processors was 20 hours.
The critical time for a job is 25 hours, and the finishing time for the schedule on 2 processors was 30 hours.
The sum of all task times for a job is 20 hours, and the finishing time for the schedule on 2 processors was 25 hours.
Based on your observations in the previous scenarios, write guidelines for when you can determine that a schedule is optimal.

Search

Text Color

Text Size

Margin Size

Font Type