14.3: The Hindu-Arabic Number System

Last updated
Save as PDF

Page ID: 34263

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The Evolution of a System

Our own number system, composed of the ten symbols {0,1,2,3,4,5,6,7,8,9} is called the Hindu-Arabic system. This is a base-ten (decimal) system since place values increase by powers of ten. Furthermore, this system is positional, which means that the position of a symbol has bearing on the value of that symbol within the number. For example, the position of the symbol 3 in the number 435,681 gives it a value much greater than the value of the symbol 8 in that same number. We’ll explore base systems more thoroughly later. The development of these ten symbols and their use in a positional system comes to us primarily from India.[i]

$Picture of Al-Biruni$ It was not until the 15^th century that the symbols that we are familiar with today first took form in Europe. However, the history of these numbers and their development goes back hundreds of years. One important source of information on this topic is the writer al-Biruni, whose picture is shown here.[ii] Al-Biruni, who was born in modern day Uzbekistan, had visited India on several occasions and made comments on the Indian number system. When we look at the origins of the numbers that al-Biruni encountered, we have to go back to the third century B.C.E. to explore their origins. It is then that the Brahmi numerals were being used.

The Brahmi numerals were more complicated than those used in our own modern system. They had separate symbols for the numbers 1 through 9, as well as distinct symbols for 10, 100, 1000,…, also for 20, 30, 40,…, and others for 200, 300, 400, …, 900. The Brahmi symbols for 1, 2, and 3 are shown below.[iii]

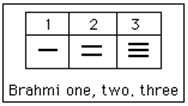
$Brahmi symbols. One is a horizontal line. Two is two horizontal lines. Three is three horizontal lines.$

These numerals were used all the way up to the 4^th century C.E., with variations through time and geographic location. For example, in the first century C.E., one particular set of Brahmi numerals took on the following form[iv]:

$First century CE Brahmi numerals. 1 to 3 are horizontal lines. 4 looks like plus, 5 like an h, 6 like a squiggle, 7 like a slanted inverted U, 8 like a sideways S, and 9 like a question mark.$

From the 4^th century on, you can actually trace several different paths that the Brahmi numerals took to get to different points and incarnations. One of those paths led to our current numeral system, and went through what are called the Gupta numerals. The Gupta numerals were prominent during a time ruled by the Gupta dynasty and were spread throughout that empire as they conquered lands during the 4^th through 6^th centuries. They have the following form[v]:

$4th through 6th century Gupta numerals. They look similar to the first century symbols, but somewhat more elaborate.$

How the numbers got to their Gupta form is open to considerable debate. Many possible hypotheses have been offered, most of which boil down to two basic types[vi]. The first type of hypothesis states that the numerals came from the initial letters of the names of the numbers. This is not uncommon…the Greek numerals developed in this manner. The second type of hypothesis states that they were derived from some earlier number system. However, there are other hypotheses that are offered, one of which is by the researcher Ifrah. His theory is that there were originally nine numerals, each represented by a corresponding number of vertical lines. One possibility is this:[vii]

$Numerals 1 through 9 represented with groupings of vertical lines.$

Because these symbols would have taken a lot of time to write, they eventually evolved into cursive symbols that could be written more quickly. If we compare these to the Gupta numerals above, we can try to see how that evolutionary process might have taken place, but our imagination would be just about all we would have to depend upon since we do not know exactly how the process unfolded.

The Gupta numerals eventually evolved into another form of numerals called the Nagari numerals, and these continued to evolve until the 11^th century, at which time they looked like this:[viii]

$11th century Nagari numerals. The 1 looks like a q, 2 and 3 look similar to the modern symbols. 4 looks like an 8, 5 looks like a 4, 6 is an elaborate squiggle, 7 is like a sideways 6, 8 like a sideways U, 9 like a curved p, and 0 like a circle.$

Note that by this time, the symbol for 0 has appeared! The Mayans in the Americas had a symbol for zero long before this, however, as we shall see later in the chapter.

These numerals were adopted by the Arabs, most likely in the eighth century during Islamic incursions into the northern part of India.[ix] It is believed that the Arabs were instrumental in spreading them to other parts of the world, including Spain (see below).

Other examples of variations up to the eleventh century include:

Devangari, eighth century[x]:

$Devangari numerals. Most look similar to modern numerals, but some are different.$

West Arab Gobar, tenth century[xi]:

$West Arab Gobar numerals. Most look similar to modern numerals, but some are different.$

Spain, 976 C.E.[xii]:

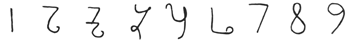
$Spanish numerals. Most look similar to modern numerals, but some are different.$

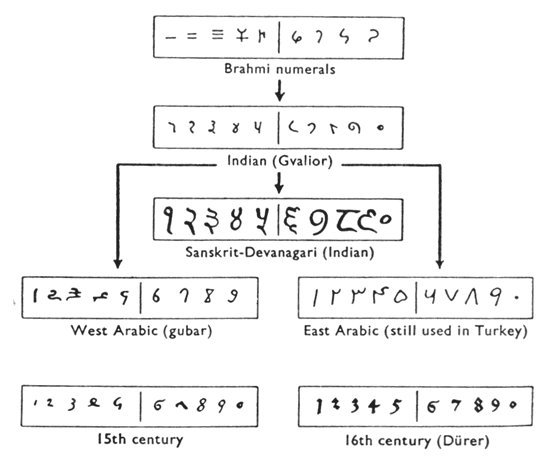
Finally, one more graphic[xiii] shows various forms of these numerals as they developed and eventually converged to the 15^th century in Europe.

$A flow chart showing the evolution of numerals from Brahmi to Indian, then splitting into three branches: West Arabic, Sanskrit-Devanagari, and East Arabic.$

The Positional System

More important than the form of the number symbols is the development of the place value system. Although it is in slight dispute, the earliest known document in which the Indian system displays a positional system dates back to 346 C.E. However, some evidence suggests that they may have actually developed a positional system as far back as the first century C.E.

The Indians were not the first to use a positional system. The Babylonians (as we will see in Chapter 3) used a positional system with 60 as their base. However, there is not much evidence that the Babylonian system had much impact on later numeral systems, except with the Greeks. Also, the Chinese had a base-10 system, probably derived from the use of a counting board[xiv]. Some believe that the positional system used in India was derived from the Chinese system.

Wherever it may have originated, it appears that around 600 C.E., the Indians abandoned the use of symbols for numbers higher than nine and began to use our familiar system where the position of the symbol determines its overall value.[xv] Numerous documents from the seventh century demonstrate the use of this positional system.

Interestingly, the earliest dated inscriptions using the system with a symbol for zero come from Cambodia. In 683, the 605^th year of the Saka era is written with three digits and a dot in the middle. The 608^th year uses three digits with a modern 0 in the middle.[xvi] The dot as a symbol for zero also appears in a Chinese work (Chiu-chih li). The author of this document gives a strikingly clear description of how the Indian system works:

Using the [Indian] numerals, multiplication and division are carried out. Each numeral is written in one stroke. When a number is counted to ten, it is advanced into the higher place. In each vacant place a dot is always put. Thus the numeral is always denoted in each place. Accordingly there can be no error in determining the place. With the numerals, calculations is easy…”[xvii]

Transmission to Europe

It is not completely known how the system got transmitted to Europe. Traders and travelers of the Mediterranean coast may have carried it there. It is found in a tenth-century Spanish manuscript and may have been introduced to Spain by the Arabs, who invaded the region in 711 C.E. and were there until 1492.

In many societies, a division formed between those who used numbers and calculation for practical, every day business and those who used them for ritualistic purposes or for state business.[xviii] The former might often use older systems while the latter were inclined to use the newer, more elite written numbers. Competition between the two groups arose and continued for quite some time.

$Drawing of two people, one using an abacus, and the other numerals.$ In a 14^th century manuscript of Boethius’ The Consolations of Philosophy, there appears a well-known drawing of two mathematicians. One is a merchant and is using an abacus (the “abacist”). The other is a Pythagorean philosopher (the “algorist”) using his “sacred” numbers. They are in a competition that is being judged by the goddess of number. By 1500 C.E., however, the newer symbols and system had won out and has persevered until today. The Seattle Times recently reported that the Hindu-Arabic numeral system has been included in the book The Greatest Inventions of the Past 2000 Years.[xix]

One question to answer is why the Indians would develop such a positional notation. Unfortunately, an answer to that question is not currently known. Some suggest that the system has its origins with the Chinese counting boards. These boards were portable and it is thought that Chinese travelers who passed through India took their boards with them and ignited an idea in Indian mathematics.[xx] Others, such as G. G. Joseph propose that it is the Indian fascination with very large numbers that drove them to develop a system whereby these kinds of big numbers could easily be written down. In this theory, the system developed entirely within the Indian mathematical framework without considerable influence from other civilizations.

[i] www-groups.dcs.st-and.ac.uk/~history/HistTopics/Indian_numerals.html

[ii] www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Al-Biruni.html

[iii] www-groups.dcs.st-and.ac.uk/~history/HistTopics/Indian_numerals.html

[iv] www-groups.dcs.st-and.ac.uk/~history/HistTopics/Indian_numerals.html

[v] Ibid

[vi] Ibid

[vii] Ibid

[viii] Ibid

[ix] Katz, page 230

[x] Burton, David M., History of Mathematics, An Introduction, p. 254-255

[xi] Ibid

[xii] Ibid

[xiii] Katz, page 231.

[xiv] Ibid, page 230

[xv] Ibid, page 231.

[xvi] Ibid, page 232.

[xvii] Ibid, page 232.

[xviii] McLeish, p. 18

[xix] seattletimes.nwsource.com/news/health-science/html98/invs_20000201.html, Seattle Times, Feb. 1, 2000

[xx] Ibid, page 232.