6.2: Enzyme Kinetics

Enzymes are catalysts, usually proteins, that help convert other molecules called substrates into products, but are themselves unchanged by the reaction. Each enzyme has high specificity for at least one reaction, and it can accelerate this reaction by millions of times. Without enzymes, most biochemical reactions are too slow for life to be possible. Enzymes are so important to our lives that a single amino acid mutation in one enzyme out of the more than 2000 enzymes in our bodies can result in a severe or lethal genetic disease.

Figure 6.1: A Michaelis-Menten reaction of two substrates converting to one product. (Drawn by User:IMeowbot, released under the GNU Free Documentation License.)

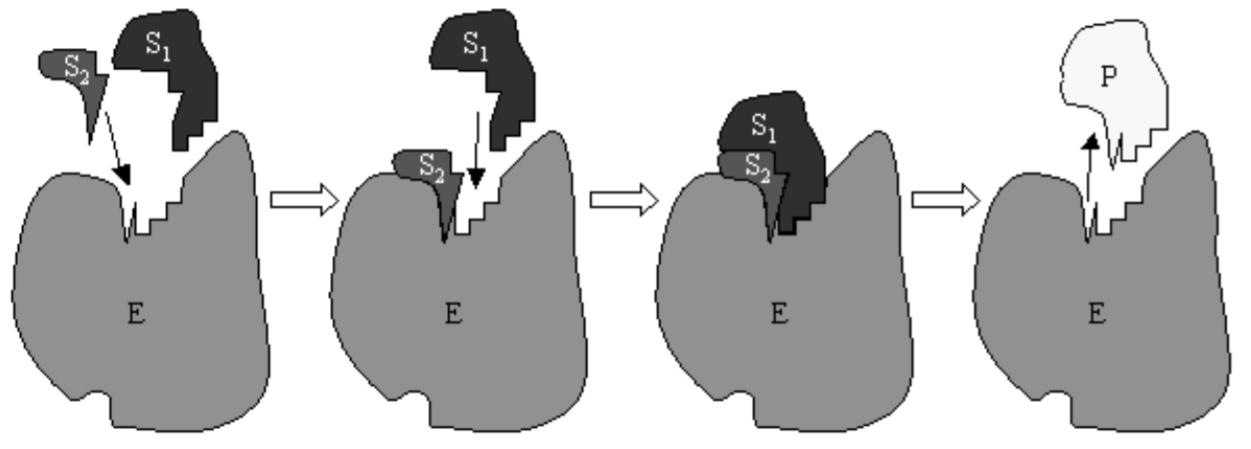
where \(C\) is a complex formed by the enzyme and the substrate. A cartoon of the Michaelis-Menten reaction with an enzyme catalyzing a reaction between two substrates is shown in Fig. 6.1. Commonly, substrate is continuously provided to the reaction and product is continuously removed. The removal of product has been modeled by neglecting the reverse reaction \(P+E \rightarrow C\). A continuous provision of substrate allows us to assume that \(S\) is held at an approximately constant concentration.

The differential equations for \(C\) and \(P\) can be obtained from the law of mass action:

\[\begin{aligned} &d C / d t=k_{1} S E-\left(k_{-1}+k_{2}\right) C \\[4pt] &d P / d t=k_{2} C . \end{aligned} \nonumber \]

Biochemists usually want to determine the reaction velocity \(d P / d t\) in terms of the substrate concentration \(S\) and the total enzyme concentration \(E_{0}\). We can eliminate \(E\) in favor of \(E_{0}\) from the conservation law that the enzyme, free and bound, is conserved; that is

\[\frac{d(E+C)}{d t}=0 \quad \Longrightarrow \quad E+C=E_{0} \quad \Longrightarrow \quad E=E_{0}-C \nonumber \]

and we can rewrite the equation for \(d C / d t\) eliminating \(E\) :

\[\begin{align} \nonumber \frac{d C}{d t} &=k_{1} S\left(E_{0}-C\right)-\left(k_{-1}+k_{2}\right) C \\[4pt] &=k_{1} E_{0} S-\left(k_{-1}+k_{2}+k_{1} S\right) C \end{align} \nonumber \]

Because \(S\) is assumed to be held constant, the complex \(C\) is expected to be in equilibrium, with the rate of formation equal to the rate of dissociation. With this so-called quasi-steady-state approximation, we may assume that \(C=0\) in \((6.3.4)\), and we have

\[C=\frac{k_{1} E_{0} S}{k_{-1}+k_{2}+k_{1} S} \nonumber \]

The reaction velocity is then given by

\[\begin{align} \nonumber \frac{d P}{d t} &=k_{2} C \\[4pt] \nonumber &=\frac{k_{1} k_{2} E_{0} S}{k_{-1}+k_{2}+k_{1} S} \\[4pt] &=\frac{V_{m} S}{K_{m}+S} \end{align} \nonumber \]

where two fundamental constants are defined:

\[K_{m}=\left(k_{-1}+k_{2}\right) / k_{1}, \quad V_{m}=k_{2} E_{0} . \nonumber \]

The Michaelis-Menten constant or the Michaelis constant \(K_{m}\) has units of concentration, and the maximum reaction velocity \(V_{m}\) has units of concentration divided by time. The interpretation of these constants is obtained by considering the following limits:

\[\begin{array}{ll} \text { as } S \rightarrow \infty, & C \rightarrow E_{0} \text { and } d P / d t \rightarrow V_{m} \\[4pt] \text { if } S=K_{m}, & C=\frac{1}{2} E_{0} \text { and } d P / d t=\frac{1}{2} V_{m} . \end{array} \nonumber \]

Therefore, \(V_{m}\) is the limiting reaction velocity obtained by saturating the reaction with substrate so that every enzyme is bound; and \(K_{m}\) is the concentration of \(S\) at which only one-half of the enzymes are bound and the reaction proceeds at one-half maximum velocity.