6.5: Cooperativity

Enzymes and other protein complexes may have multiple binding sites, and when a substrate binds to one of these sites, the other sites may become more active. A well-studied example is the binding of the oxygen molecule to the hemlobin protein. Hemoglobin can bind four molecules of \(\mathrm{O}_{2}\), and when three molecules are bound, the fourth molecule has an increased affinity for binding. We call this cooperativity.

We will model cooperativity by assuming that an enzyme has two separated but indistinguishable binding sites for a substrate \(S\). For example, the enzyme may

Figure 6.4: Cooperativity.

be a protein dimer, composed of two identical sub-proteins with identical binding sites for \(S\). A cartoon of this enzyme is shown in Fig. 6.4. Because the two binding sites are indistinguishable, we need consider only two complexes: \(C_{1}\) and \(C_{2}\), with enzyme bound to one or two substrate molecules, respectively. When the enzyme exhibits cooperativity, the binding of the second substrate molecule has a greater rate constant than the binding of the first. We therefore consider the following reaction:

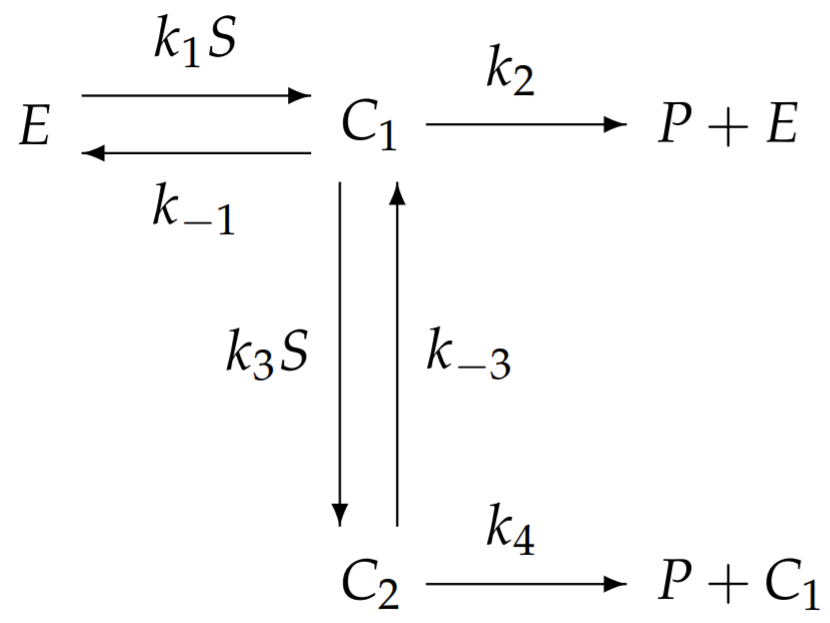
where cooperativity supposes that \(k_{1} \ll k_{3}\). Application of the law of mass action results in

\[\begin{aligned} \frac{d C_{1}}{d t} &=k_{1} S E+\left(k_{-3}+k_{4}\right) C_{2}-\left(k_{-1}+k_{2}+k_{3} S\right) C_{1} \\[4pt] \frac{d C_{2}}{d t} &=k_{3} S C_{1}-\left(k_{-3}+k_{4}\right) C_{2} \end{aligned} \nonumber \]

Applying the quasi-equilibrium approximation \(\dot{C}_{1}=\dot{C}_{2}=0\) and the conservation law \(E_{0}=E+C_{1}+C_{2}\) results in the following system of two equations and two unknowns:

\[\begin{align} \left(k_{-1}+k_{2}+\left(k_{1}+k_{3}\right) S\right) C_{1}-\left(k_{-3}+k_{4}-k_{1} S\right) C_{2} &=k_{1} E_{0} S, \\[4pt] k_{3} S C_{1}-\left(k_{-3}+k_{4}\right) C_{2} &=0 . \end{align} \nonumber \]

We divide \((6.5.1)\) by \(k_{1}\) and \((6.5.2)\) by \(k_{3}\) and define

\[K_{1}=\frac{k_{-1}+k_{2}}{k_{1}}, \quad K_{2}=\frac{k_{-3}+k_{4}}{k_{3}}, \quad \epsilon=k_{1} / k_{3} \nonumber \]

to obtain

\[\begin{align} \left(\epsilon K_{1}+(1+\epsilon) S\right) C_{1}-\left(K_{2}-\epsilon S\right) C_{2} &=\epsilon E_{0} S, \\[4pt] S C_{1}-K_{2} C_{2} &=0 . \end{align} \nonumber \]

We can subtract (6.5.5) from (6.5.4) and cancel \(\epsilon\) to obtain

\[\left(K_{1}+S\right) C_{1}+S C_{2}=E_{0} S . \nonumber \]

Equations (6.5.5) and (6.5.6) can be solved for \(C_{1}\) and \(C_{2}\) :

\[\begin{align} C_{1} &=\frac{K_{2} E_{0} S}{K_{1} K_{2}+K_{2} S+S^{2}} \\[4pt] C_{2} &=\frac{E_{0} S^{2}}{K_{1} K_{2}+K_{2} S+S^{2}} \end{align} \nonumber \]

so that the reaction velocity is given by

\[\begin{align} \frac{d P}{d t} &=k_{2} C_{1}+k_{4} C_{2} \\[4pt] &=\frac{\left(k_{2} K_{2}+k_{4} S\right) E_{0} S}{K_{1} K_{2}+K_{2} S+S^{2}} \end{align} \nonumber \]

To illuminate this result, we consider two limiting cases: (i) no cooperativity, where the active sites act independently so that each protein dimer, say, can be considered as two independent protein monomers; (ii) strong cooperativity, where the binding of the second substrate has a much greater rate constant than the binding of the first.

Independent active sites

Figure 6.5: The reaction velocity \(d P / d t\) as a function of the substrate \(S\). Shown are the solutions to the Hill equation with \(V_{m}=1, K_{m}=1\), and for \(n=1,2\).

Therefore, for independent active sites, the reaction velocity becomes

\[\begin{aligned} \frac{d P}{d t} &=\frac{\left(2 k_{2} K_{m}+2 k_{2} S\right) E_{0} S}{K_{m}^{2}+2 K_{m} S+S^{2}} \\[4pt] &=\frac{2 k_{2} E_{0} S}{K_{m}+S} \end{aligned} \nonumber \]

The reaction velocity for a dimer protein enzyme composed of independent identical monomers is simply double that of a monomer protein enzyme, an intuitively obvious result.

Strong cooperativity

We now assume that after the first substrate binds to the enzyme, the second substrate binds much more easily, so that \(k_{1} \ll k_{3}\). The number of enzymes bound to a single substrate molecule should consequently be much less than the number bound to two substrate molecules, resulting in \(C_{1} \ll C_{2}\). Dividing (6.5.7) by (6.5.8), this inequality becomes

\[\frac{C_{1}}{C_{2}}=\frac{K_{2}}{S} \ll 1 . \nonumber \]

Dividing the numerator and denominator of \((6.5.9)\) by \(S^{2}\), we have

\[\frac{d P}{d t}=\frac{\left(k_{2} K_{2} / S+k_{4}\right) E_{0}}{\left(K_{1} / S\right)\left(K_{2} / S\right)+\left(K_{2} / S\right)+1} . \nonumber \]

To take the limit of this expression as \(K_{2} / S \rightarrow 0\), we set \(K_{2} / S=0\) everywhere except in the first term in the denominator, since \(K_{1} / S\) is inversely proportional to \(k_{1}\) and may go to infinity in this limit. Taking the limit and multiplying the numerator and denominator by \(S^{2}\),

\[\frac{d P}{d t}=\frac{k_{4} E_{0} S^{2}}{K_{1} K_{2}+S^{2}} \nonumber \]

Here, the maximum reaction velocity is \(V_{m}=k_{4} E_{0}\), and the modified MichaelisMenten constant is \(K_{m}=\sqrt{K_{1} K_{2}}\), so that

\[\frac{d P}{d t}=\frac{V_{m} S^{2}}{K_{m}^{2}+S^{2}} \nonumber \]

In biochemistry, this reaction velocity is generalized to

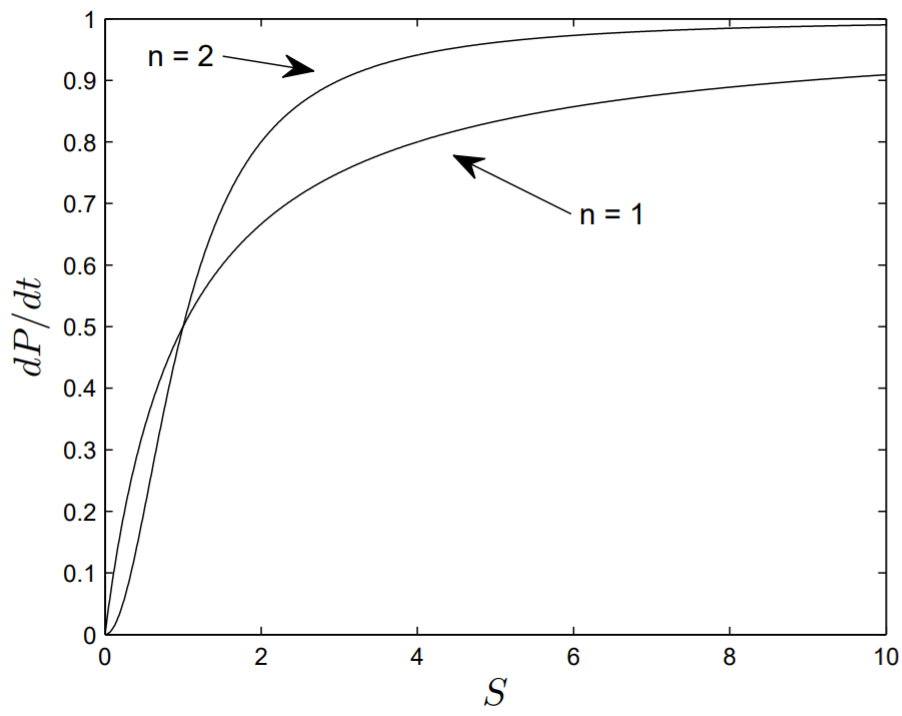
\[\frac{d P}{d t}=\frac{V_{m} S^{n}}{K_{m}^{n}+S^{n}} \nonumber \]

known as the Hill equation, and by varying \(n\) is used to fit experimental data.

In Fig. \(6.5\), we have plotted the reaction velocity \(d P / d t\) versus \(S\) as obtained from the Hill equation with \(n=1\) or 2 . In drawing the figure, we have taken both \(V_{m}\) and \(K_{m}\) equal to unity. It is evident that with increasing \(n\) the reaction velocity more rapidly saturates to its maximum value.