6.4: Allosteric Inhibition

Last updated
Save as PDF

Page ID: 93519

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The term allostery comes from the Greek word allos, meaning different, and stereos, meaning solid, and refers to an enzyme with a regulatory binding site separate from its active binding site. In our model of allosteric inhibition, an inhibitor molecule is assumed to bind to its own regulatory site on the enzyme, resulting in either a lowered binding affinity of the substrate to the enzyme, or a lowered conversion rate of substrate to product. A cartoon of allosteric inhibition due to a lowered binding affinity is shown in Fig. $6.3$.

In general, we need to define three complexes: $C_{1}$ is the complex formed from substrate and enzyme; $C_{2}$ from inhibitor and enzyme, and; $C_{3}$ from substrate, inhibitor, and enzyme. We write the chemical reactions as follows:

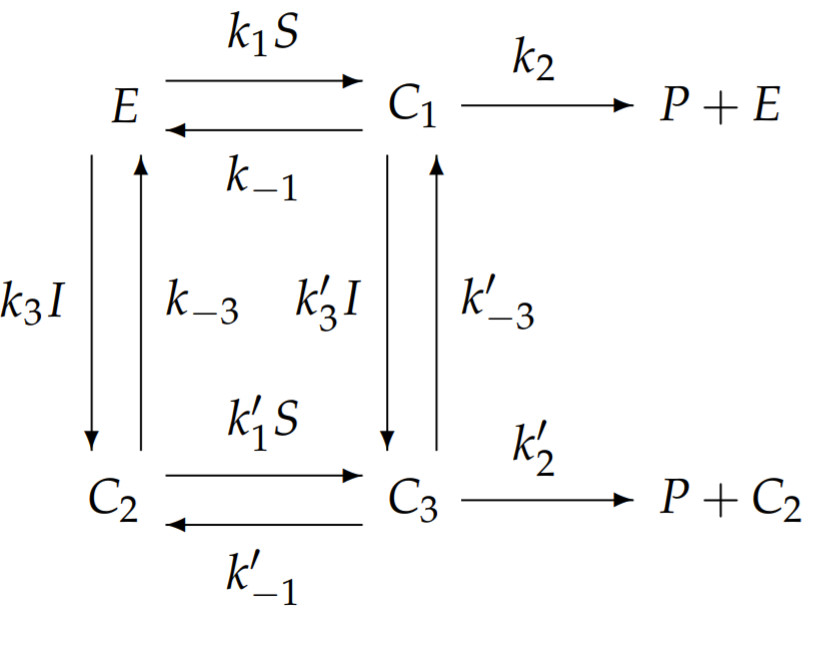
$clipboard_e7c6048933a68c0850cd297b12417b071.png$

The general model for allosteric inhibition with ten independent rate constants appears too complicated to analyze. We will simplify this general model to one with fewer rate constants that still exhibits the unique features of allosteric inhibition. One possible but uninteresting simplification assumes that if $I$ binds to $E$, then $S$ does not; however, this reduces allosteric inhibition to competitive inhibition and loses the essence of allostery. Instead, we simplify by allowing both $I$ and $S$ to simultaneously bind to $E$, but we assume that the binding of I prevents substrate conversion to product. With this simplification, $k_{2}^{\prime}=0$. To further reduce the number of independent rate constants, we assume that the binding of $S$ to $E$ is unaffected by the bound presence of $I$, and the binding of $I$ to $E$ is unaffected by the bound presence of $S$. These approximations imply that all the primed rate constants equal the corresponding unprimed rate constants, e.g., $k_{1}^{\prime}=k_{1}$, etc. With these simplifications, the schematic of the chemical reaction simplifies to

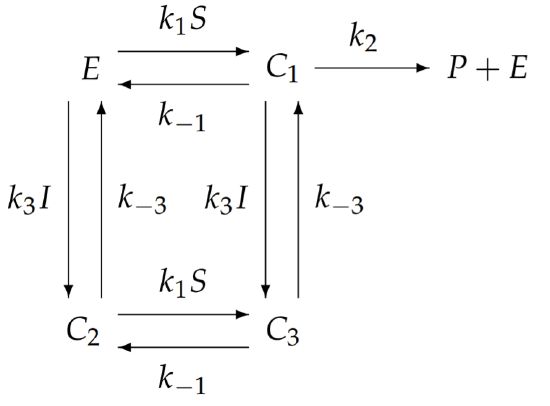
$clipboard_eaf907d6091b64c4a42b2f90c6571d8ac.png$

and now there are only five independent rate constants. We write the equations for the complexes using the law of mass action:

\[\begin{align} &\frac{d C_{1}}{d t}=k_{1} S E+k_{-3} C_{3}-\left(k_{-1}+k_{2}+k_{3} I\right) C_{1} \\[4pt] &\frac{d C_{2}}{d t}=k_{3} I E+k_{-1} C_{3}-\left(k_{-3}+k_{1} S\right) C_{2} \\[4pt] &\frac{d C_{3}}{d t}=k_{3} I C_{1}+k_{1} S C_{2}-\left(k_{-1}+k_{-3}\right) C_{3} \end{align} \nonumber \]

while the reaction velocity is given by

\[\frac{d P}{d t}=k_{2} C_{1} \nonumber \]

Again, both free and bound enzyme is conserved, so that $E=E_{0}-C_{1}-C_{2}-C_{3}$. With the quasi-equilibrium approximation $\dot{C}_{1}=\dot{C}_{2}=\dot{C}_{3}=0$, we obtain a system of three equations and three unknowns: $C_{1}, C_{2}$ and $C_{3} .$ Despite our simplifications, the analytical solution for the reaction velocity remains messy (see Keener & Sneyd, referenced at the chapter’s end) and not especially illuminating. We omit the complete analytical result here and determine only the maximum reaction velocity.

The maximum reaction velocity $V_{m}^{\prime}$ for the allosteric-inhibited reaction is defined as the time-derivative of the product concentration when the reaction is saturated With substrate; that is,

\[\begin{aligned} V_{m}^{\prime} &=\lim _{S \rightarrow \infty} d P / d t \\[4pt] &=k_{2} \lim _{S \rightarrow \infty} C_{1} \end{aligned} \nonumber \]

With substrate saturation, every enzyme will have its substrate binding site occupied. Enzymes are either bound with only substrate in the complex $C_{1}$, or bound together with substrate and inhibitor in the complex $C_{3}$. Accordingly, the schematic of the chemical reaction with substrate saturation simplifies to

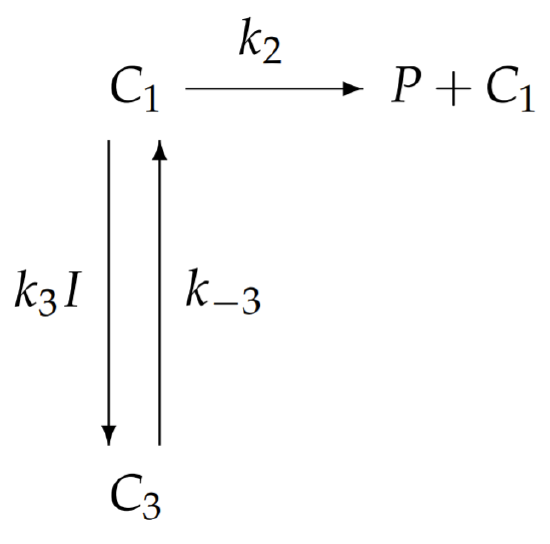
$clipboard_e440294fbb66b8045d534adf265bfc3fd.png$

The equations for $C_{1}$ and $C_{3}$ with substrate saturation are thus given by

\[\begin{align} \frac{d C_{1}}{d t} &=k_{-3} C_{3}-k_{3} I C_{1} \\[4pt] \frac{d C_{3}}{d t} &=k_{3} I C_{1}-k_{-3} C_{3} \end{align} \nonumber \]

and the quasi-equilibrium approximation yields the single independent equation

\[\begin{align} \nonumber C_{3} &=\left(k_{3} / k_{-3}\right) I C_{1} \\[4pt] &=\left(I / K_{i}\right) C_{1} \end{align} \nonumber \]

with $K_{i}=k_{-3} / k_{3}$ as before. The equation expressing the conservation of enzyme is given by $E_{0}=C_{1}+C_{3}$. This conservation law, together with $(6.4.7)$, permits us to solve for $C_{1}$ :

\[C_{1}=\frac{E_{0}}{1+I / K_{i}} \nonumber \]

Therefore, the maximum reaction velocity for the allosteric-inhibited reaction is given by

\[\begin{aligned} V_{m}^{\prime} &=\frac{k_{2} E_{0}}{1+I / K_{i}} \\[4pt] &=\frac{V_{m}}{1+I / K_{i}} \end{aligned} \nonumber \]

where $V_{m}$ is the maximum reaction velocity of both the uninhibited and the competitive inhibited reaction. The allosteric inhibitor is thus seen to reduce the maximum velocity of the uninhibited reaction by the factor $\left(1+I / K_{i}\right)$, which may be large if the concentration of allosteric inhibitor is substantial.