1.31: Right Triangle Trigonometry

Last updated
Save as PDF

Page ID: 153135

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

a white ladder leaning on a red wall, casting it shadow — Photo by Georgios Karamanis on flickr.

You may use a calculator throughout this module.

The word “trigonometry” essentially means the measurement of triangles. In this module, we will focus on right triangles. If we know some information about a right triangle, such as the measure of one side and one angle, we can use trigonometry to determine the measure of another side.

Sine, Cosine, Tangent

Consider one of the acute angles in a right triangle.

The sine of the angle is the ratio of the opposite side to the hypotenuse.
The cosine of the angle is the ratio of the adjacent side to the hypotenuse.
The tangent of the angle is the ratio of the opposite side to the adjacent side.

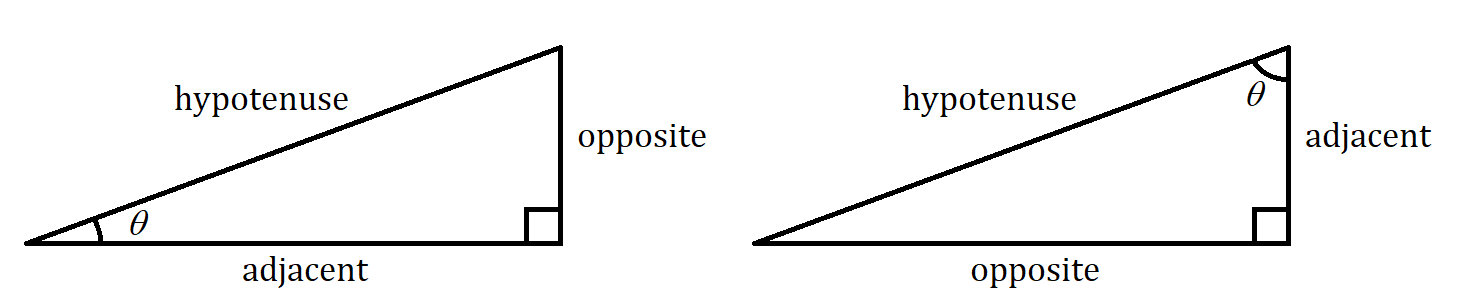
$a right triangle with lower left acute angle marked, bottom side labeled 'adjacent', right side labeled 'opposite', upper left side labeled 'hypotenuse' and another right triangle with upper right acute angle marked, right side labeled 'adjacent', bottom side labeled 'opposite', upper left side labeled 'hypotenuse'$

SOHCAHTOA

sine = $\dfrac{\text{opposite}}{\text{hypotenuse}}$

cosine = $\dfrac{\text{adjacent}}{\text{hypotenuse}}$

tangent = $\dfrac{\text{opposite}}{\text{adjacent}}$

Exercises

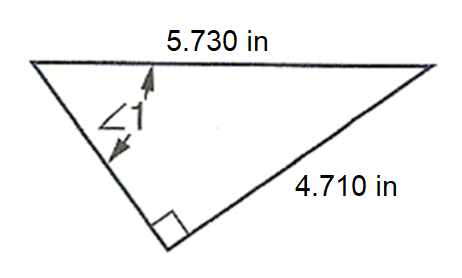
In relation to $\angle{1}$, identify which side of the triangle is the adjacent side, the opposite side, and the hypotenuse.

$right triangle with lower left acute angle marked 1, then going counterclockwise, side marked e, right angle, side marked f, unmarked acute angle, side marked d.$
$right triangle with northeast acute angle marked 1, then going counterclockwise, side marked x, right angle, side marked y, unmarked acute angle, side marked r.$

Now let’s look at a specific example, a right triangle with sides of length 3, 4, and 5. Measuring the angles with a protractor will show us that the smaller acute angle is approximately $37^\circ$ and the larger acute angle is $53^\circ$; to the nearest hundredth of a degree, these values are $36.87^\circ$ and $53.13^\circ$.

Exercises

Use the diagram to determine each of the following, first as a fraction and then as a decimal (rounded to four significant figures, if necessary).
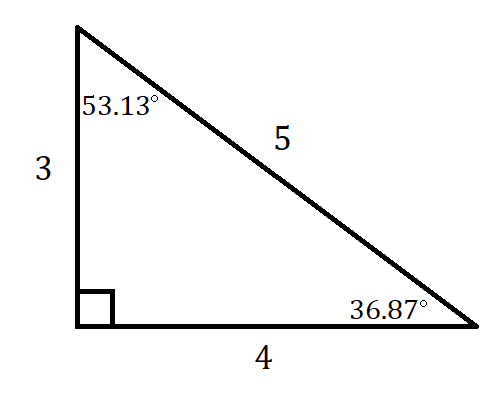
$right triangle with lower right angle marked 36.87 degrees, upper left angle marked 53.13 degrees; left side labeled 3, bottom side labeled 4, upper right side labeled 5$

sin $36.87^\circ$
cos $36.87^\circ$
tan $36.87^\circ$
sin $53.13^\circ$
cos $53.13^\circ$
tan $53.13^\circ$

Note that we would have gotten the same results for any right triangle whose sides are in the ratio 3:4:5. If the sides had been 6, 8, 10, the angles measures would still be $36.87^\circ$ and $53.13^\circ$. If the sides had been 30, 40, 50, the angles measures would still be $36.87^\circ$ and $53.13^\circ$.

Or to look at it another way, any right triangle with angles $36.87^\circ$ and $53.13^\circ$ will have these relationships: the shorter leg is $\dfrac{3}{5}$ the hypotenuse, the longer leg is $\dfrac{4}{5}$ the hypotenuse, and the shorter leg is $\dfrac{3}{4}$ the longer leg. Your scientific calculator knows this and is programmed with all the trigonometric values you need.

Exercises

Use your calculator to determine each of the following as a decimal (rounded to four significant figures, if necessary). Be sure that your calculator is in degree mode, not radian mode, before you begin.

sin $36.87^\circ$
cos $36.87^\circ$
tan $36.87^\circ$
sin $53.13^\circ$
cos $53.13^\circ$
tan $53.13^\circ$

You may notice some repeated answers here, which makes sense because, for example, the side opposite the $53.13^\circ$ angle is adjacent to the $36.87^\circ$ angle, which means that sin $53.13^\circ$ must be equal to cos $36.87^\circ$.

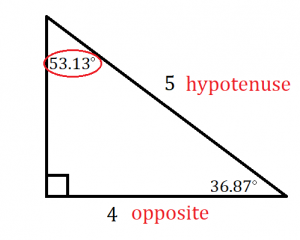
$right triangle with right angle in the southwest, 53.13 degree angle circled in the northwest, bottom side labeled 4 opposite, upper right side labeled 5 hypotenuse$ $right triangle with right angle in the southwest, 36.87 degree angle circled in the southeast, bottom side labeled 4 adjacent, upper right side labeled 5 hypotenuse$

Trigonometry Applications

The sine, cosine, and tangent ratios apply to any right triangle, not just a 3-4-5 triangle, which is what makes trigonometry so useful. If we know the measure of one side and one acute angle in a right triangle, we can use SOHCAHTOA to find the length of another side of the triangle. For each of the following exercises, we’ll need to decide whether the parts we’re dealing with will require us to use sine, cosine, or tangent.

Exercises

Determine the length of the labeled unknown side of each right triangle. Round each answer appropriately.

$right triangle with southeast acute angle marked 28.8 degrees, then going clockwise, side marked z, right angle, unmarked side, unmarked acute angle, side marked 5.3 cm.$
$right triangle with southeast acute angle marked 28.8 degrees, then going clockwise, unmarked side, right angle, side marked g, unmarked acute angle, side marked 5.3 cm.$
$right triangle with lower left acute angle marked 40 degrees 0 minutes, then going counterclockwise, side marked 6.800 in, right angle, side marked b, unmarked acute angle, unmarked side.$
$right triangle with left acute angle marked 45.80 degrees, then going counterclockwise, side marked 52.64 mm, right angle, unmarked side, unmarked acute angle, side marked p.$
$right triangle with upper left acute angle marked 62.70 degrees, then going counterclockwise, side marked y, right angle, side marked 263.80 mm, unmarked acute angle, unmarked side.$
$right triangle with northwest acute angle marked 62.70 degrees, then going counterclockwise, unmarked side, right angle, side marked 263.80 mm, unmarked acute angle, side marked d.$
A guy wire is attached to a utility pole. The wire is anchored to the ground 15 feet from the base of the pole, forming a $56^\circ$ angle with the level ground. What is the length of the wire, to the nearest foot?
A 19-foot ladder is leaning against a wall, forming a $70^\circ$ angle with the level ground. What is the vertical height of the place where the ladder contacts the wall?
During intermission of a hockey game, one lucky fan gets to shoot a puck from the blue line at the goal, 64 feet away, for the chance to win a team jersey. Actually, there is a sheet of fabric blocking the entire goal except for a 6-inch wide hole in the bottom center. If the fan shoots the puck hard enough, aiming directly at the center of the hole, they win. If their aim is off by $1^\circ$, will they still win the jersey? (If it helps, a hockey puck is 3 inches in diameter.)

$Hockey-Fan.png$

Inverse Sine, Inverse Cosine, Inverse Tangent

Okay, we now know how to find the length of a side if we know an angle and another side. But what if we know the lengths of the sides and want to determine a missing angle? Rather than carefully making a scale drawing and using a protractor, we can use a calculator.

Your calculator’s SIN, COS, and TAN keys take an angle measure for the input and give a ratio (in decimal form) as the output. Your calculator’s $\text{SIN}^{-1}$, $\text{COS}^{-1}$, and $\text{TAN}^{-1}$ keys allow you to work backwards; they take a ratio for the input and give an angle measure for the output.

Exercises

Use your calculator to determine each of the following angle measures (rounded to the nearest hundredth of a degree, if necessary).

$\text{sin}^{-1}\left(\dfrac{3}{5}\right)$
$\text{cos}^{-1}\left(\dfrac{1}{2}\right)$
$\text{tan}^{-1}\left(\dfrac{4}{3}\right)$

Inverse Trigonometry Applications

Exercises

Determine the measure of the marked angle. Round each answer to the nearest hundredth of a degree.

$right triangle with southwest acute angle marked A, then going counterclockwise, side marked 2.300 in, right angle, side marked 1.700 in, unmarked acute angle, unmarked slanted side.$
$right triangle with southeast acute angle marked 1, then going clockwise, side marked 4.360 in, right angle, unmarked side, unmarked acute angle, slanted side marked 5.870 in.$
$right triangle with southwest acute angle marked 1, then going counterclockwise, unmarked side, right angle, side marked 4.45 mm, unmarked acute angle, slanted side marked 8.70 mm.$
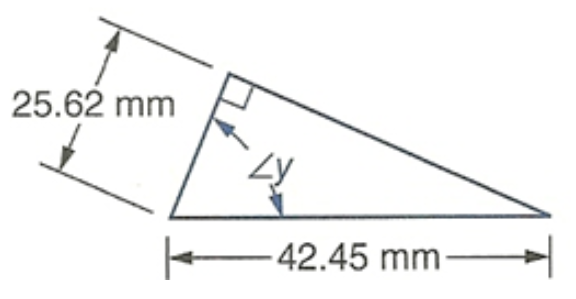
$right triangle with southwest acute angle marked y, then going clockwise, side marked 25.62 mm, right angle, unmarked side, unmarked acute angle, side marked 42.45 mm.$
$right triangle with northwest acute angle marked 1, then going counterclockwise, unmarked side, right angle, side marked 4.710 in, unmarked acute angle, side marked 5.730 in.$
$right triangle with northwest acute angle marked x, then going counterclockwise, side marked 17.070 in, right angle, side marked 10.460 in, acute angle marked y, unmarked side.$
A rule of thumb for ladder safety is that the vertical height where the ladder touches the wall should be four times the horizontal distance from the base of the ladder to the wall.^[1] To the nearest degree, what is the angle between the ladder and the floor in this scenario?
The entrance to a public building is 2 feet higher than the courtyard in front of the entrance. A ramp is being constructed, continuous with no switchbacks or level platforms, with a surface length of 25 feet. ADA regulations^[2] limit the angle of elevation to a maximum of approximately $4.75^\circ$. Does the ramp’s design meet ADA standards?

smiling young woman in wheelchair wearing green dress — Photo by UNDP in Europe and Central Asia on flickr.

Using Multiple Methods

In Module 18, we used the Pythagorean Theorem, $a^2 + b^2 = c^2$, to determine the length of an unknown side in a right triangle. We can use the Pythagorean Theorem in conjunction with trigonometry to solve a problem in more than one way or to double-check our results.

Exercises

$right triangle with southwest acute angle marked A, then counterclockwise, horizontal leg marked 14, right angle, vertical leg marked 17, unmarked angle, hypotenuse marked h$

First, use inverse tangent to determine the value of $A$. Round to the nearest tenth of a degree.
Next, use sine with $\angle A$ to determine the value of $h$. Round to the nearest tenth.
Next, use cosine with $\angle A$ to determine the value of $h$. Round to the nearest tenth.
Finally, use the Pythagorean Theorem to determine the value of $h$. Round to the nearest tenth.
Compare your answers for Exercises 36-38. Are they the same or are they different?

$Wallowa-Lake-Tramway-Sign-2.png$

The Wallowa Lake Tramway in Eastern Oregon carries passengers along a $9,650\text{ ft}$ cable, with a vertical rise of $3,700\text{ ft}$. Although the cable is not straight along its entire length, let’s assume that it is. To the nearest degree, what is the angle of elevation of the cable?
What is the approximate horizontal run covered by the tramway cable?

$Wallowa-Lake-Tram-Summit.jpg$

Source: www.americanladderinstitute.org/page/Ladders101↵
This is implied at https://www.ada-compliance.com/ada-compliance/ada-ramp but not directly stated. We'll verify this angle measure in the next module. ↵

Search

Text Color

Text Size

Margin Size

Font Type

Exercises

Exercises

Exercises

Exercises

Exercises

Exercises

Exercises