1.5: Homework
- Page ID
- 70301
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Submit homework separately from this workbook and staple all pages together. (One staple for the entire submission of all the unit homework)
- Start a new module on the front side of a new page and write the module number on the top center of the page.
- Answers without supporting work will receive no credit.
- Some solutions are given in the solutions manual.
- You may work with classmates but do your own work.
Let U = {a, c, e, m n, r, u, v, w, x, z} with subsets A, B, C and D defined below: A = {m, n, r, u, x} B = { a, c , r, u, x} C = {e, v, w, x, z } D = {a, c, z} Using correct notation, find the following, show all work
| a. \(\bf B \cap D\) | f. \(\bf A - C^{c}\) | k. \(\bf (A \cap D) - B^{c}\) |
| b. \(\bf A \cap D\) | g. \(\bf B - (A \cap C)\) | l. n(\(\bf A \cup B\)) |
| c. C - B | h. \(\bf D^{c} - (B \cup C)\) | m. n(A) + n(B) |
| d. \(\bf (A \cup C)^{c}\) | i. \(\bf (A \cap B) \cap (C \cup D)\) | n. n(D - C) |
| e. \(\bf D^{c} \cap B\) | j. \(\bf (B^{c} \cup D)^{c}\) | o. n(\(\bf B \cap C\)) |
Let U = {a, c, e, m n, r, u, v, w, x, z} with subsets A, B, C defined as follows:
| A = {m, n, r, u, v} | B = {r, u, w, x} | C = {n, r, x, c} |
Draw a Venn Diagram and place each element of the universe in the correct region
Use deMorgan's Laws to rewrite each of the following:
| a. \(\bf N \cup P^{c}\) | b. \(\bf R^{c} \cap S\) |
Use the distributive properties of sets to rewrite each of the following:
| a. \(\bf (A^{c} \cup E) \cap (A^{c} \cup F)\) | b. \(\bf B \cap (A \cup C)\) |
A survey was given to determine which of the three beverages (tea, milk and/or coffee) people drank each day. The results were as follows:
| 7 only drank coffee | 6 drank all three | 11 drank tea and coffee |
| 21 drank coffee | 4 drank none of the three | 9 drank neither coffee or tea |
| 21 drank tea | 1 drank only tea and milk |
| a. Draw a Venn diagram indicating how many people would belong in each region. Label the three sets with meaningful letters. |
| b. How many people were surveyed? |
| c. How many drank milk? |
| d. How many drank only coffee and milk? |
| e. How many drank only milk? |
| f. How many drank tea or coffee but not milk? |
| g. How many drank exactly two kinds of beverages? |
| h. How many didn’t drink milk or tea? |
Take out your A–blocks and arrange them into subsets so that each subset only contains elements that have the same size and color.
| a. How many subsets are there? | b. How many pieces are in each subset? |
Let A, B and C represent any sets. Answer True or False for the following statements. In order for a statement to be true, it must always be true. For each False statement, give an example of why it is False.
| a. B is always a subset of \(\bf A \cup B\) |
| b. \(\bf (A - B)^{c} = A^{c} - B^{c}\) |
| c. B is always a subset of \(\bf A \cap B\) |
| d. \(n\)(\(\bf A \cup B\)) = \(n\)(A) + \(n\)(B) |
| e. \(n\)(\(\bf A \cup B)\) = \(n\)(A) + \(n\)(B) – \(n\)(\(\bf A \cap B\)) |
| f. If \(n\)(\(\bf A \cup B\)) = \(n\)(A) + \(n\)(B), then A and B are disjoint. |
Draw a Venn diagram and shade in the region that represents the following
| a. \(\bf (C \cup A) - B\) | b. \(\bf (C \cap B) \cup A\) | c. \(\bf (C \cap B) - A\) |
| d. \(\bf (A \cup C) \cap B\) | e. \(\bf \bar{A} - (B \cap C)\) | f. \(\bf (B - A) \cap (B - C)\) |
Identify the shaded area of each Venn diagram by set notation.
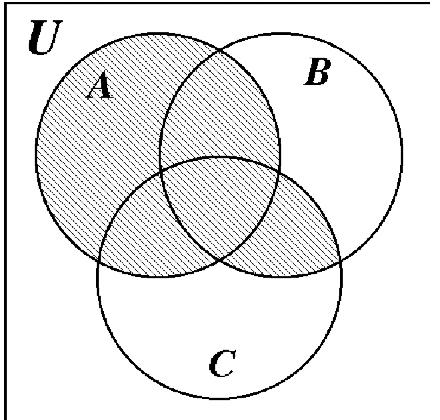 a. a. |
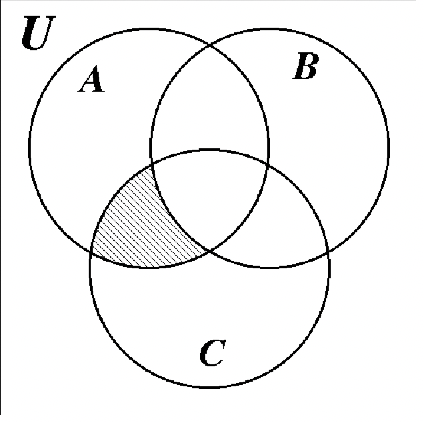 b. b. |
List all possible subsets for each set given.
| a. { } | b. {a} | c. {a, b} | d. {a, b, c} |
Let A = {1, 2, 4}, B = {(a, c), 5} and C = {x}. Find the following:
| a. \(A \times A\) | a. \(A \times B\) | c. \(B \times C\) |
| d. \(C \times A\) | a. \(C \times C\) |
Use your A–blocks to do this problem. Let X represent the set of large circles and Y represent the set of red circles. Using set notation and abbreviations, find the following:
| a. X - Y | b. \(\bf X \cap Y\) | c. \(\bf X \cup Y\) | d. Y - X |


