3.2: Combining

You will need: Base Blocks (Material Cards 4-15)

We will begin this exercise set by figuring out how to add in the Egyptian numeral system. You are reminded of the symbols and their Hindu-Arabic equivalents below:

| (1)

(10)

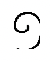(100)

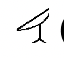(1,000)

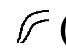(10,000)

(100,000)

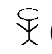(1,000,000)

Since the Egyptian numeration system is a basic additive system, the sum of two numbers is formed by simply combiningthe symbols from both numerals together. Because it is a Base Ten system, an exchange can be made any time there are ten of the same symbol by replacing ten of one symbol for the next higher symbol . To show that an exchange is being made, you can circle, put a box around or underline ten of the same symbol. In the examples that follow, the exchanges are indicated by putting a box around a group of ten symbols that are to be replaced with a new symbol at the next step. After each exchange, it may be necessary to make another exchange. Study the following examples of Egyptian addition problems. Try to think in Egyptian as you do these by simply following the rules of combining and exchanging as opposed to thinking about what numbers each numeral stands for in Hindu-Arabic. After working through each problem, you can always go back and check by first converting each of the numerals being added (the addends )to Hindu-Arabic, adding them together and then checking that the sum agrees with the answer obtained in Egyptian.

Exercise 1

Add the following Egyptian numerals. Show all steps, indicating any exchanges made. Again, try to work through these by thinking only in Egyptian. You can always go back and check when you are done by doing them in Hindu-Arabic. Make up your own problems for part e and part f.

a.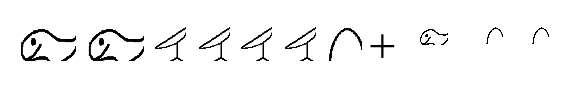

b.

c.

d.

Let’s pretend that our current system of money was strictly in Base Ten so that the only currency we used were pennies, dimes, one dollar bills, ten dollar bills, hundred dollar bills, thousand dollar bills and so on. Instead of drawing pictures of the money, these abbreviations for each kind of coin or bill will be used: penny (A), dime (B), one dollar bill (C), ten dollar bill (D), hundred dollar bill (E), thousand dollar bill (F) and so on. Since most of you are considering entering the teaching profession, you probably won’t need to handle anything higher than a thousand dollar bill. At least that’s the case as I write this in 1999 but who knows what the future holds, right?

Exercise 2

Show what exchanges could be made for each of the following:

a. AAAAAAAAAA = ____

b. CCCCCCCCCC = ____

c. FFFFFFFFFF = ____

Exercise 3

Form each sum by combining the two addends into one lump. Make exchanges as necessary so that the sum is represented by the least number of coins or bills. Show all steps, indicating any exchanges made.

a. CCAADDDCB + BBBBBBBBBAAACC

b. AAAACCCCCCCCCEEE + CCCCCCBBA

c. EEEEEEEEAAAAAAAA + EEEAA

d. DDDDCCCCCBBBBB + DDDDDCCCCBBBBB

To add in the Mayan system, the first step is to combine the symbols at each level together. The symbols at each level must be combined separately. Then, at each level, look to see if any exchanges can be made. A group of five dots can always be exchanged for a line segment. Exchanges from one level to the next are a little trickier. A group of 20 at one level can be traded for one dot at the next level up except from the second to the third level where a group of 18 at the second level can be traded for one dot at the third level. Study the following examples of one level Mayan numerals being added together. Any time an exchange is being made, a circle or box will be put around what will be replaced at the next step. An arrow will be used to indicate if an exchange is being made from one level to the next level up. The arrow indicates a dot will be on the next level up in the next step in place of the amount boxed at the original level. See example 2 below: From step 2 to step 3, the four line segments on level one are replaced with a dot at level two.

Example 1

Example 2

Example 3

Example 4

Exercise 4

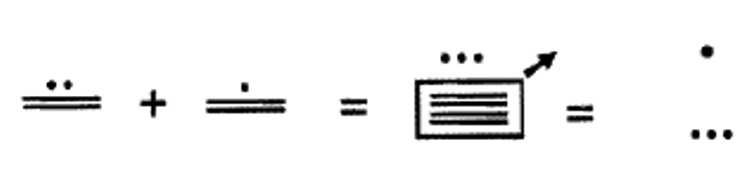
Add the following single level Mayan numerals together. Make any necessary exchanges and show all steps.

a.

b.

c.

Study the following examples on this and the next page of adding Mayan numerals together. All of these are more than one level. Large spaces are used to differentiate between the different levels. Try to do them by yourself on your own paper.

Example 1

Example 2

Example 3

Remember, a group of 18 at the second level can be exchanged for a dot at the third level!

Example 4

Example 5

After doing each of the above examples solely in Mayan, I checked each problem by converting each addend to Hindu-Arabic, adding in Base Ten, converting the sum into Mayan and making sure the answer agreed with the answer I had gotten. When I checked Example 5 (76,896 + 46,754 = 123,650), a fairly complicated problem, it didn't check. So I reworked the problem until I got it right. It's a good idea to check your work carefully as you go along which requires strong doses of concentration, effort and patience. Otherwise, it's quite easy to make one or more mistakes during computation. Keep in mind that if all you do is convert to Hindu-Arabic, add and convert back to Mayan, you won't get credit because that would not show all of the steps involved, combining, exchanging, etc. that you are required to show when you do the exercises. Try each of the above examples on a separate piece of paper to make sure you are working them correctly. Note that the sequence of steps shown for each example might not be the only way to arrive at the correct answer.

Exercise 5

Add the following Mayan numerals together. Make any necessary exchanges and show all steps. It's a very good idea to check your work and that doesn't mean looking up the answer in the solutions! After adding in Mayan, convert the answer to Hindu-Arablic. Then, convert the original two numbers to Hindu-Arabic and add together and see if it matches the answer.

a.

b.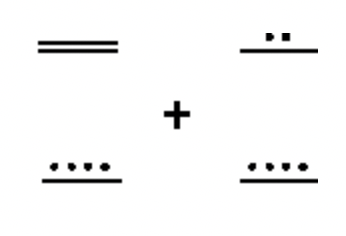

c.

d.

e.

Exercise 6

Count out 15 unit blocks and make exchanges with base four blocks. Put them in a pile, called Pile A, and SAVE THIS PILE. Since you've made exchanges in base four, write 15 as a base four numeral on the space provided for Pile A below. Now, count out 13 more units and make exchanges with base four blocks. Put them in a pile, called Pile B. Since you've made exchanges in base four, write 13 as a base four numeral on the space provided for Pile B below. To add, simply combine the blocks from Pile A and Pile B to form one big pile of blocks. You are forming the union of Pile A and Pile B! Make all possible exchanges with base four blocks and then write the number of units in the combined pile as a base four numeral on the space provided.

Combining the two piles is the same as forming the sum of the two numerals. You have just added two numbers together in a different base.

Below is the addition problem you have just performed in Base Four.

____________ + _____________ = ____________

Pile A Pile B Combined Pile

Exercise 7

Count out 15 unit blocks and make exchanges with base seven blocks. Put them in a pile, called Pile A, and SAVE THIS PILE. Since you've made exchanges in base seven , write 15 as a base seven numeral on the space provided for Pile A below. Now, count out 13 more units and make exchanges with base seven blocks. Put them in a pile, called Pile B. Since you've made exchanges in base seven , write 13 as a base seven numeral on the space provided for Pile B below. To add, simply combine the blocks from Pile A and Pile B to form one big pile of blocks. You are forming the union of Pile A and Pile B! Make all possible exchanges with base seven blocks and then write the number of units in the combined pile as a base seven numeral on the space provided below.

Combining the two piles is the same as forming the sum of the two numerals. You have just added two numbers together in a different base.

Below is the addition problem you have just performed in Base Seven

____________ + _____________ = ____________

Pile A Pile B Combined Pile

Exercise 8

Count out 15 unit blocks and make exchanges with base two blocks. Put them in a pile, called Pile A, and SAVE THIS PILE. Since you've made exchanges in base two, write 15 as a base two numeral on the space provided for Pile A below. Now, count out 13 more units and make exchanges with base two blocks. Put them in a pile, called Pile B. Since you've made exchanges in base two, write 13 as a base two numeral on the space provided for Pile B below. To add, simply combine the blocks from Pile A and Pile B to form one big pile of blocks. You are forming the union of Pile A and Pile B! Make all possible exchanges with base two blocks and then write the number of units in the combined pile as a base two numeral on the space provided.

Combining the two piles is the same as forming the sum of the two numerals. You have just added two numbers together in a different base.

Below is the addition problem you have just performed in Base Two.

____________ + _____________ = ____________

Pile A Pile B Combined Pile

Exercise 9

Count out 15 unit blocks and make exchanges with base nine blocks. Put them in a pile, called Pile A, and SAVE THIS PILE. Since you've made exchanges in base nine, write 15 as a base nine numeral on the space provided for Pile A below. Now, count out 13 more units and make exchanges with base nine blocks. Put them in a pile, called Pile B. Since you've made exchanges in base nine, write 13 as a base nine numeral on the space provided for Pile B below. To add, simply combine the blocks from Pile A and Pile B to form one big pile of blocks. You are forming the union of Pile A and Pile B! Make all possible exchanges with base nine blocks and then write the number of units in the combined pile as a base nine numeral on the space provided.

Combining the two piles is the same as forming the sum of the two numerals. You have just added two numbers together in a different base.

Below is the addition problem you have just performed in Base Nine.

____________ + _____________ = ____________

Pile A Pile B Combined Pile

Exercise 10

Count out 15 unit blocks and make exchanges with base three blocks. Put them in a pile, called Pile A, and SAVE THIS PILE. Since you've made exchanges in base three, write 15 as a base three numeral on the space provided for Pile A below. Now, count out 13 more units and make exchanges with base three blocks. Put them in a pile, called Pile B. Since you've made exchanges in base three, write 13 as a base three numeral on the space provided for Pile B below. To add, simply combine the blocks from Pile A and Pile B to form one big pile of blocks. You are forming the union of Pile A and Pile B! Make all possible exchanges with base three blocks and then write the number of units in the combined pile as a base three numeral on the space provided below.

Combining the two piles is the same as forming the sum of the two numerals. You have just added two numbers together in a different base.

Below is the addition problem you have just performed in Base Three

____________ + _____________ = ____________

Pile A Pile B Combined Pile

Exercise 11

Count out 15 unit blocks and make exchanges with base eight blocks. Put them in a pile, called Pile A, and SAVE THIS PILE. Since you've made exchanges in base eight, write 15 as a base eight numeral on the space provided for Pile A below. Now, count out 13 more units and make exchanges with base eight blocks. Put them in a pile, called Pile B. Since you've made exchanges in base eight, write 13 as a base eight numeral on the space provided for Pile B below. To add, simply combine the blocks from Pile A and Pile B to form one big pile of blocks. You are forming the union of Pile A and Pile B! Make all possible exchanges with base eight blocks and then write the number of units in the combined pile as a base eight numeral on the space provided below.

Combining the two piles is the same as forming the sum of the two numerals. You have just added two numbers together in a different base.

Below is the addition problem you have just performed in Base Eight.

____________ + _____________ = ____________

Pile A Pile B Combined Pile

Exercise 12

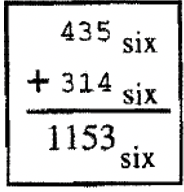
Write the six addition problems from exercises 6 -11 in a vertical format like the one in Base Six shown below. Study this Base Six problem as well as all six problems from the previous six exercises. Try to figure out a way to do the addition problems using paper and pencil instead of by using the Base Blocks. In other words, try to come up with your own algorithm (method) for doing addition in other bases. Explain your method and show a few examples. In the next Exercise Set, you will be learning algorithms for addition.

Let m < b and n < b. Let's define the word "complement" of a number, \(m_{b}\), in a given base b to be the number, \(n_{b}\), such \(m_{b} + n_{b} = 10_{b}\). (Don't read 10b as "ten, base b"). In other words, think of mb as a number of single units less than the base, b. Then the complement, nb, would be the number of single units it takes to add to mb such that the sum of mb and nb could be traded in for exactly one long. Note: Complement as defined here has nothing to do with the word complement as we defined and used it in Set Theory! The examples on the next page should clarify this definition.

Here are some examples of complements. The base must be specified.

In Base Ten: 3 & 7 are complements since 3 + 7 = 10

4 & 6 are complements since 4 + 6 = 10

8 is the complement of 2 since 8 + 2 = 10

5 is the complement of 5 since 5 + 5 = 10

In Base Eight: the complement of \(5_{\text{eight}}\) is 3\(_{\text{eight}}\) since 5\(_{\text{eight}}\) + 3\(_{\text{eight}}\) = 10\(_{\text{eight}}\)

4\(_{\text{eight}}\) & 4\(_{\text{eight}}\) are complements since 4\(_{\text{eight}}\) + 4\(_{\text{eight}}\) = 10\(_{\text{eight}}\)

2\(_{\text{eight}}\) & 6\(_{\text{eight}}\) are complements since 2\(_{\text{eight}}\) + 6\(_{\text{eight}}\) = 10\(_{\text{eight}}\)

7\(_{\text{eight}}\) is the complement of 1\(_{\text{eight}}\) since 7\(_{\text{eight}}\) + 1\(_{\text{eight}}\) = 10\(_{\text{eight}}\)

Exercise 13

Write the complement of each number:

a. \(7_{\text{nine}}\)	b. \(5_{\text{seven}}\)	c. \(2_{\text{tweleve}}\)
d. \(3_{\text{eleven}}\)	e. \(2_{\text{six}}\)	f. \(1_{\text{two}}\)
g. \(2_{\text{three}}\)	h. \(1_{\text{four}}\)	i. \(3_{\text{five}}\)

Although not necessarily a conscious effort, many people use complements and the associative property of addition to add. For instance, some people use the following strategy to add in Base Ten. Let's say the problem was to add 8 and 6. A person might think "I have 8 and it only takes 2 more to get to 10. If I take 2 from the 6 and add it to the 8, then I have 10 + 4 which is 14" In other words, the problem 8 + 6 becomes 8 + (2 + 4) = (8 + 2) + 4 = 10 + 4 = 14. Of course, they do it more automatically than it looks when written down.

The same type of strategy can be used in other bases. Study the following examples. It might help if you use units and longs in the Base Blocks.

\(4_{\text{nine}} + 8_{\text{nine}} = 4_{\text{nine}} + (5_{\text{nine}} + 3_{\text{nine}}\))
= (\(4_{\text{nine}} + 5_{\text{nine}}) + 3_{\text{nine}}\)
= \(10_{\text{nine}} + 3_{\text{nine}}\)
= \(13_{\text{nine}}\) (which is 1 long and 3 units in base nine)

\(T_{\text{twelve}} + 9_{\text{twelve}} = T_{\text{twelve}} + (2_{\text{twelve}} + 7_{\text{twelve}}\))
= (\(T_{\text{twelve}} + 2_{\text{twelve}}) + 7_{\text{twelve}}\)
= \(10_{\text{twelve}} + 7_{\text{twelve}}\)
= \(17_{\text{twelve}}\) (which is 1 long and 7 units in base twelve)

\(4_{\text{six}} + 4_{\text{six}} = 4_{\text{six}} + (2_{\text{six}} + 2_{\text{six}}\))
= (\(4_{\text{six}} + 2_{\text{six}}) + 2_{\text{six}}\)
= \(10_{\text{six}} + 2_{\text{six}}\)
= \(12_{\text{six}}\) (which is 1 long and 2 units in base six)

Exercise 14

Use your Base Blocks or the definition of complements to do the following addition problems:

a. \(7_{\text{eleven}} + 8_{\text{eleven}}\)	b. \(4_{\text{five}} + 3_{\text{five}}\)
c. \(2_{\text{eight}} + 7_{\text{eight}}\)	d. \(9_{\text{thirteen}} + 5_{\text{thirteen}}\)
e. \(3_{\text{four}} + 3_{\text{four}}\)	f. \(6_{\text{seven}} + 4_{\text{seven}}\)
g. \(2_{\text{three}} + 2_{\text{three}}\) =	h. \(1_{\text{two}} + 1_{\text{two}}\)
i. \(3_{\text{six}} + 5_{\text{six}}\)	j. \(7_{\text{nine}} + 5_{\text{nine}}\)

Now that you can add single digit numbers in any base, you can make up addition tables. Below are addition tables in Base Five and Base Eight. Since Base Five has five digits, its addition table should be a five by five grid and since Base Eight has eight digits, its addition table should be a eight by eight grid. Notice how symmetry, the commutative property and the property that x + 0 = x for all x makes much of the table easy to fill in. When making addition tables (and later when making multiplication tables) in different bases, you should label what kind of a table it is. If you do that, then the convention will be that it is not necessary to write out the word for what base it is to the right of each numeral.

Table \(\PageIndex{1}\): Base Five Addition Table

+	0	1	2	3	4
0	0	1	2	3	4
1	1	2	3	4	10
2	2	3	4	10	11
3	3	4	10	11	12
4	4	10	11	12	13

Table \(\PageIndex{2}\): Base Eight Addition Table

+	0	1	2	3	4	5	6	7
0	0	1	2	3	4	5	6	7
1	1	2	3	4	5	6	7	10
2	2	3	4	5	6	7	10	11
3	3	4	5	6	7	10	11	12
4	4	5	6	7	10	11	12	13
5	5	6	7	10	11	12	13	14
6	6	7	10	11	12	13	14	15
7	7	10	11	12	13	14	15	16

Exercise 15

Make up addition tables in the base specified.

a. Base Three Addition Table

b. Base Six Addition Table

c. Base Two Addition Table