7.1: The Meaning of Division
- Page ID
- 70323
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)You will need: Centimeter Strips (Material Cards 16A-16L) and Base Blocks (Material Cards 3 - 15)
In these first few exercises, you'll be using c-strips to explore division.
In this first exercise, we will divide \(H \div Y\). H, the part before the division sign, is called the DIVIDEND, and Y, the part after the division sign, is called the DIVISOR. One way to do this division is to find the maximum number of times the divisor (Y) can be subtracted from the dividend (H). Take out a hot pink c-strip (H). To figure out how many yellow c-strips could be subtracted, make a train consisting of as many yellow c-strips (Y) as possible such that the train you make is shorter or equal to the length of H, and if you were to add one more yellow c-strip, the train would be longer than the hot pink c-strip.
a. How many yellow c-strips did you use? ______
This number is called the QUOTIENT.
The quotient is the maximum number of times the divisor can be subtracted from the dividend.
b. If the train you made is shorter than H, what color c-strip could
you add to that train to make it equal in length to the hot pink c-strip? ______
This piece, which must be shorter than the divisor, is called the REMAINDER.
Put the hot pink strip next to the train you formed. It should look like this:
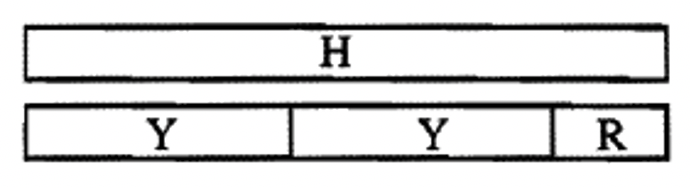
To compute \(H \div Y\), we need to figure out what goes in the blanks to make the equation in part c, below, true. The first blank must contain the largest c-strip possible that will make the equation true, and the second blank must be shorter than the yellow c-strip. We made a train of yellows, with at most one extra piece to form the length of H. Notice this is a train of yellows (which can be formed into a rectangle) plus an extra piece. Form the two yellow strips into a rectangle and find the c-strip that goes across the width. That c-strip goes in the first blank, and the extra piece (R) goes in the second blank. Fill in the blanks of the equation below. This equation should make sense by looking at the picture above showing H and the train are the same length.
c. H = ____ \(\cdots Y\) + ____
The QUOTIENT is in bold, and the REMAINDER is underlined.
We can now conclude that: \(H \div Y\) = \(\mathbf{R}\) remainder \(\underline{R}\), since \(H = \mathbf{R} \cdots Y\) + \(\underline{R}\)
This can be written as a statement about numbers by translating each c-strip to a number.
Using numbers in the above equation, \(12 \div 5\) = \(\mathbf{2}\) remainder \(\underline{2}\), since 12 = \(\mathbf{2} \cdots 5\) + \(\underline{2}\)
For a - e, do the division using the c-strips to make a train of as many of the divisor as possible such that the length of the train you make is less than or equal to the length of the dividend, and if you were to add one more of the divisor to the train, it would be longer than the dividend. If the train ends up being the same length as the dividend, there will be no remainder and the second blank will be empty. Draw a diagram showing the c-strip that is the dividend and under it, draw the train you formed. Do this the same way we did it for exercise 1. Follow the example below.
\(H \div Y\) = \(\mathbf{R}\) remainder \(\underline{R}\), since H = \(\mathbf{R}\) \(\cdots\) Y + \(\underline{R}\)
\(12 \div 5\) = \(\mathbf{2}\) remainder \(\underline{2}\), since 12 = \(\mathbf{2}\) \(\cdots\) 5 + \(\underline{2}\)
Show diagram below:
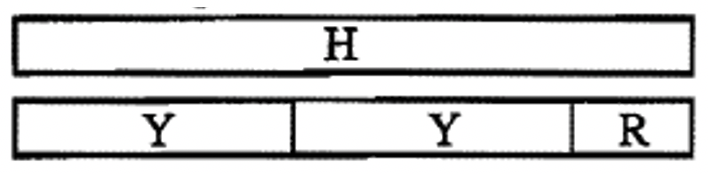
|
a. \(B \div R:\) \( B \div R\) = __ remainder __ since B = __ \(\cdots\) R + __ __ \(\div\) __ = __ remainder __ since __ = __ \(\cdots\) __ + __ Show diagram below: |
|
b. S \(\div\) L: S \(\div\) L = __ remainder __ since S = __ \(\cdots\) L + __ __ \(\div\) __ = __ remainder __ since __ = __ \(\cdots\) __ + __ Show diagram below: |
|
c. \(N \div P:\) \( N \div P\) = __ remainder __ since N = __ \(\cdots\) P + __ __ \(\div\) __ = __ remainder __ since __ = __ \(\cdots\) __ + __ Show diagram below: |
|
d. \(K \div P:\) \( K \div P\) = __ remainder __ since K = __ \(\cdots\) P + __ __ \(\div\) __ = __ remainder __ since __ = __ \(\cdots\) __ + __ Show diagram below: |
|
e. \(D \div L:\) \( D \div L\) = __ remainder __ since D = __ \(\cdots\) L + __ __ \(\div\) __ = __ remainder __ since __ = __ \(\cdots\) __ + __ Show diagram below: |
Count out 36 unit blocks. How would you divide the 36 blocks by 2? Explain how you would do it, and show a picture of what you did. What is the answer?
Get out your base four blocks now, and trade in 36 units for a number in base four.
a. Write 36 as a base four numeral: _____________
Decide how to divide this by 2 using base four blocks.
b. Explain how you would do it, and show a picture of what you did.
c. What is the answer in base four? _________
d. Write the division problem and the quotient (answer) in base four: ____________\( \div 2_{\text{four}}\) = ____________
Get out your base three blocks now, and trade in 36 units for a number in base three.
a. Write 36 as a base three numeral: _____________
Decide how to divide this by 2 using base three blocks.
b. Explain how you would do it, and show a picture of what you did.
c. What is the answer in base three? _________
d. Write the division problem and the quotient (answer) in base three: ____________\( \div 2_{\text{three}}\) = ____________
Count out 36 unit blocks. How would you divide the 36 blocks by 3? Explain how you would do it, and show a picture of what you did. What is the answer?
Get out your base four blocks now, and trade in 36 units for a number in base four.
a. Write 36 as a base four numeral: _____________
Decide how to divide this by 3 using base four blocks.
b. Explain how you would do it, and show a picture of what you did.
c. What is the answer in base four? _________
d. Write the division problem and the quotient (answer) in base four: ____________\( \div 3_{\text{four}}\) = ____________
Count out 48 unit blocks. How would you divide the 48 blocks by 16? Explain how you would do it, and show a picture of what you did. What is the answer?
There are two basic ways of thinking about division. The two word problems below both require the division \(18 \div 3\), but the problems are really quite different.
If you have 18 cookies and want to divide the cookies up equally amongst your three children, how many cookies should you give to each child?
If you have 18 cookies and want to make baggies having three cookies in each to put in lunch boxes, how many baggies will you be able to make?
Both require the division problem \(18 \div 3\), and the answer to each problem is 6. But the picture used to solve each is very different.
In Word Problem A, you are told how many kids there are, and you are asked to figure out how many cookies each child should be given. Imagine 3 children in front of you. You need to disburse the cookies amongst the 3 children so that each receives the same number of cookies. To begin, you might draw a model to represent three kids. It might look something like this:

You know there are 3 kids and each will be given the same number of cookies so that the total number of cookies they all have is 18. After disbursing, you might show the picture like this:

This is a way to illustrate that each of the 3 children has 6 cookies. If you prefer, you can actually draw 6 dots or 6 cookies in each circle. It's up to you.
Note that if you look at the model drawn, it is simply the multiplication problem 3 \(\cdots\) 6, since there are 3 sets of 6 added together. The interpretation of division Word Problem A represents is called:
Partitioning into (Equal) Subsets
In this interpretation, the divisor is the number of subsets in which to disburse something. The dividend, 18, must be divided amongst 3 equal subsets (3 is the divisor). The quotient (answer to the division problem) will be the number of elements (6) placed in each subset (the kids, in this case.) The task is to partition 18 cookies into 3 equal subsets. In this interpretation, you are given how many subsets there are (from reading the problem in this case, each kid represents one subset), but you do not how many are in each subset (that is the question being asked in this case, how many cookies each child should receive). You do the division to figure out how many elements will end up in each subset. After doing the division, the number of elements IN each subset is the answer to the problem.
One way to distinguish that a problem is suggesting this interpretation is to consider whether the information in the problem provides you with the number of subsets. If it does, as in Word Problem A, then it is the partitioning into equal subsets interpretation.
Okay, let's look at Word Problem B now.
If you have 18 cookies and want to make baggies having three cookies in each to later put in lunch boxes, how many baggies will you be able to make?
In Word Problem B, you don’t know how many subsets there will be. In fact, you are being asked how many subsets you will be able to make, so the partitioning into subsets interpretation wouldn't apply.
What you do know is how many of something will be in each subset. You would place three cookies in a baggie, then 3 more in another baggie, and so on. You won’t know how many subsets you will have until you finish disbursing the cookies. You would take three cookies away at a time and put them in a baggie, until you ran out of cookies. After doing this, a picture you might draw to illustrate this procedure might look like this:

Again, if you prefer to show three dots in each circle, as opposed to just writing the numeral 3, in each circle, that is perfectly fine. Either way, it should be clear from the drawing what procedure was used.
After disbursing all the cookies, you would count up how many baggies you were able to make, and that would give you the answer. Note the answer is 6, in this case. The model shown represents the multiplication \(6 \cdots 3\), since there are 6 baggies of 3 cookies each.
The interpretation of division Word Problem B represents is called:
Repeated Subtraction
In this interpretation, the divisor is the number of elements that will go into each subset. Each time the divisor (3) is subtracted from the dividend (18), a subset is formed. After all elements have been disbursed, the quotient (answer) is found by counting how many subsets were formed. This interpretation is used when you are given how many elements are in each subset, and you are trying to find out how many subsets can be made (that is the question being asked). You do the division (by using repeated subtraction) to figure out how many subsets can be made. After doing the division, the number of subsets you made is the answer to the problem.
One way to distinguish that a problem is suggesting this interpretation is to consider whether the information in the problem provides you with how many elements go into a subset. If so, as in Word Problem B, then it is the repeated subtraction interpretation.
Word Problems requiring division generally fall into the category of Repeated Subtraction or Partitioning into Subsets. After reading a word problem, you should be able to analyze and interpret it as a problem that requires Partitioning into Subsets or Repeated Subtraction to solve the problem, and then be able to draw a picture using that interpretation. Also, for any division problem given, you should be able to write two distinct word problems, one for each interpretation, and draw a picture for each interpretation, and be able to explain and show all the steps necessary to solve the problem.
Terry wanted to divide 100 marbles amongst his three best friends and himself. How many marbles would each of them get?
- What division problem do you need to do to find the answer?
- What interpretation of division does this word problem represent?
- Explain how to use the correct interpretation to draw a picture to find the answer.
- Draw a picture using the correct interpretation to help find the answer.
- Write the multiplication problem shown by the picture:
- Explain how you use the picture to find the answer to the problem. Be specific.
- What is the answer to this problem? ______
Jordan made 80 ounces of jello, and wanted to put them in 8 ounce containers. How many containers can she fill?
- What division problem do you need to do to find the answer?
- What interpretation of division does this word problem represent?
- Explain how to use the correct interpretation to draw a picture to find the answer.
- Draw a picture using the correct interpretation to help find the answer.
- Write the multiplication problem shown by the picture:
- Explain how you use the picture to find the answer to the problem. Be specific.
- What is the answer to this problem? ______
Angie had 144 pages of blank paper. She was making copies of a 16 page short story she wrote to send to magazines. How many complete copies could she make?
- What division problem do you need to do to find the answer?
- What interpretation of division does this word problem represent?
- Explain how to use the correct interpretation to draw a picture to find the answer.
- Draw a picture using the correct interpretation to help find the answer.
- Write the multiplication problem shown by the picture:
- Explain how you use the picture to find the answer to the problem. Be specific.
- What is the answer to this problem? ______
A group of four friends pooled their money together for some lottery tickets and won $500. How much does each person receive from the winnings?
- What division problem do you need to do to find the answer?
- What interpretation of division does this word problem represent?
- Explain how to use the correct interpretation to draw a picture to find the answer.
- Draw a picture using the correct interpretation to help find the answer.
Sheila wanted to make as many cakes from a recipe requiring 1\(\frac{1}{3}\) cups of flour for each cake. She had 8 cups of flour. How many cakes could she make?
- What division problem do you need to do to find the answer?
- What interpretation of division does this word problem represent?
- Explain how to use the correct interpretation to draw a picture to find the answer.
- Draw a picture using the correct interpretation to help find the answer.
- Write the multiplication problem shown by the picture:
- Explain how you use the picture to find the answer to the problem. Be specific.
- What is the answer to this problem? ______
Tom won 65 baseballs and decided to divide them up evenly amongst the 13 boys on his baseball team. How many baseballs will each kid get?
- What division problem do you need to do to find the answer?
- What interpretation of division does this word problem represent?
- Explain how to use the correct interpretation to draw a picture to find the answer.
- Draw a picture using the correct interpretation to help find the answer.
- Write the multiplication problem shown by the picture:
- Explain how you use the picture to find the answer to the problem. Be specific.
- What is the answer to this problem? ______
If you are not presented with a word problem, but are simply given a division problem, you can use either interpretation to think about and solve the problem. Many times, it is easier to use one interpretation over another, especially if you need to draw a picture to show how you solved the problem.
Consider the following division problem: \(26 \div 2\). Let’s say the 26 represented 2 pennies. Would it be easier to partition 26 pennies into 2 piles and count how many are in each pile; or would it be easier to make several equal subsets containing 2 pennies each from the 26 pennies, and then to count how many subsets there are? The picture you draw to represent each interpretation is quite different. Look at the difference:
A picture using partitioning into equal subsets interpretation is shown below:
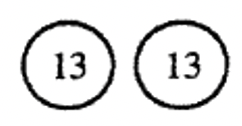
A picture using the Repeated Subtraction interpretation is shown below:
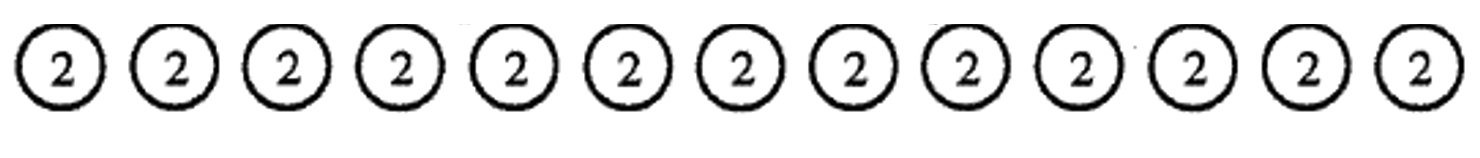
For parts a - h of this exercise, consider the division problem: \(\bf 48 \div 12\).
- Which interpretation do you think would be easier to use if you needed to draw a picture?
- Explain why the interpretation you chose in part a would be easier to use.
- Make up a word problem requiring the division \(48 \div 12\), such that the partitioning into subsets interpretation is used. Make sure your problem asks a question!
- Draw a picture to solve your problem using the Partitioning into Subsets interpretation:
- The multiplication for the picture shown in part d is: ____________________
- Make up a word problem requiring the division \(48 \div 12\), such that the repeated subtraction interpretation is used. Make sure your problem asks a question!
- Draw a picture to solve your problem using the Repeated Subtraction interpretation:
- The multiplication for the picture shown in part g is: ____________________
For parts a - h of this exercise, consider the division problem: \(\bf 200 \div 4\).
- Which interpretation do you think would be easier to use if you needed to draw a picture?
- Explain why the interpretation you chose in part a would be easier to solve this division problem. Contrast it with the other interpretation.
- Make up a word problem requiring the division \(200 \div 4\), such that the partitioning into subsets interpretation is used. Make sure your problem asks a question!
- Draw a picture to solve your problem using the Partitioning into Subsets interpretation:
- The multiplication for the picture using Partitioning into Subsets is: ________
- Make up a word problem requiring the division \(200 \div 4\), such that the repeated subtraction interpretation is used. Make sure your problem asks a question!
- Explain what you would have to do if you had to draw a picture to solve your problem using the Repeated Subtraction interpretation. Do not actually draw the picture — just explain.
- The multiplication for a picture using Repeated Subtraction would be:
For parts a - h of this exercise, consider the division problem: \( 150 \div 50\).
- Which interpretation do you think would be easier to use if you needed to draw a picture?
- Explain why the interpretation you chose in part a would be easier to solve this division problem. Contrast it with the other interpretation.
- Make up a word problem requiring the division \(150 \div 50\), such that the partitioning into subsets interpretation is used. Make sure your problem asks a question!
- Explain what you would have to do if you had to draw a picture to solve your problem using the Partitioning into Subsets interpretation. Do not actually draw the picture — just explain!
- The multiplication for a picture using Partitioning into Subsets would be: ____
- Make up a word problem requiring the division \(150 \div 50\), such that the repeated subtraction interpretation is used. Make sure your problem asks a question!
- Draw a picture to solve your problem using the Repeated Subtraction interpretation:
- The multiplication for the picture using Repeated Subtraction is: ___________
For parts a - h of this exercise, consider the division problem: \(\bf 140 \div 35\).
- Which interpretation do you think would be easier to use if you needed to draw a picture?
- Explain why the interpretation you chose in part a would be easier to solve this division problem. Contrast it with the other interpretation.
- Make up a word problem requiring the division \(140 \div 35\), such that the partitioning into subsets interpretation is used. Make sure your problem asks a question!
- Explain what you would have to do if you had to draw a picture to solve your problem using the Partitioning into Subsets interpretation. Do not actually draw the picture — just explain!
- The multiplication for a picture using Partitioning into Subsets would be: ____
- Make up a word problem requiring the division \(140 \div 35\), such that the repeated subtraction interpretation is used. Make sure your problem asks a question!
- Draw a picture to solve your problem using the Repeated Subtraction interpretation:
- The multiplication for the picture using Repeated Subtraction is:
For parts a - h of this exercise, consider the division problem: \(\bf 95 \div 5\).
- Which interpretation do you think would be easier to use if you needed to draw a picture?
- Explain why the interpretation you chose in part a would be easier to solve this division problem. Contrast it with the other interpretation.
- Make up a word problem requiring the division \(95 \div 5\), such that the partitioning into subsets interpretation is used. Make sure your problem asks a question!
- Draw a picture to solve your problem using the Partitioning into Subsets interpretation:
- The multiplication for the picture using Partitioning into Subsets is: ________
- Make up a word problem requiring the division \(95 \div 5\), such that the repeated subtraction interpretation is used. Make sure your problem asks a question!
- Explain what you would have to do if you had to draw a picture to solve your problem using the Repeated Subtraction interpretation. Do not actually draw the picture — just explain!
- The multiplication for a picture using Repeated Subtraction would be: ______
For parts a - h of this exercise, consider the division problem: \(\bf 800 \div 160\).
- Which interpretation do you think would be easier to use if you needed to draw a picture?
- Explain why the interpretation you chose in part a would be easier to solve this division problem. Contrast it with the other interpretation.
- Make up a word problem requiring the division \(800 \div 160\), such that the partitioning into subsets interpretation is used. Make sure your problem asks a question!
- Explain what you would have to do if you had to draw a picture to solve your problem using the Partitioning into Subsets interpretation. Do not actually draw the picture — just explain!
- The multiplication for a picture using Partitioning into Subsets would be: ____
- Make up a word problem requiring the division \(800 \div 160\), such that the repeated subtraction interpretation is used. Make sure your problem asks a question!
- Draw a picture to solve your problem using the Repeated Subtraction interpretation:
- The multiplication for the picture using Repeated Subtraction is:
For each division problem, a picture is shown. Based on the picture, state which interpretation of division was used.
|
a. \(84 \div 21\) Interpretation: _______ 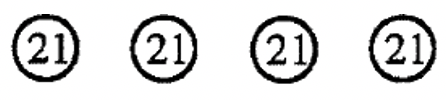 |
|
b. \(85 \div 5\) Interpretation: _______  |
|
c. \(30 \div 5\) Interpretation: _______  |
|
d. \(30 \div 6\) Interpretation: _______  |
For each picture, a particular interpretation of division was used to solve a division problem. Based on the interpretation and picture, decide what the original division problem was, and circle the correct one of the two choices given.
|
a. Repeated Subtraction  Circle the correct division problem: \(56 \div 8\) or \(56 \div 7\) |
|
a. Repeated Subtraction  Circle the correct division problem: \(56 \div 8\) or \(56 \div 7\) |
For each picture, a particular interpretation of division was used to solve a division problem. Based on that interpretation and picture, state the original division problem.
|
a. Partitioning into Subsets 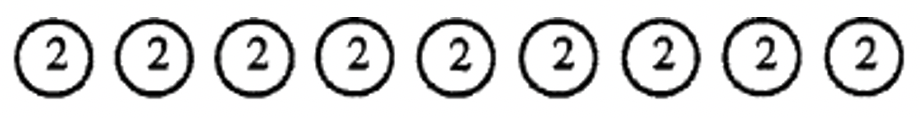 If partitioning into subsets was used, state the division problem: ___________ |
|
b. Repeated Subtraction 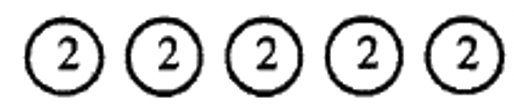 If repeated subtraction was used, state the division problem: ___________ |
If you drew a picture for the multiplication problem, a \(\cdot\) b, which letter represents how subsets are made, and which letter represents how many are in each subset?
Division is the operation that undoes mutiplication. Students can rely on this fact to learn basic division facts. For instance, since 6 \(\cdot\) 7 = 42, then \(42 \div 6 = 7\) and \(42 \div 7 = 6\). Below is a formal definition of division
Definition: a \(\div\) b is defined to be the unique number, c, under the following conditions: \(a \div b = c\) if and only if a = b \(\cdot\) c. If there is no number, c, that exists, or if there is more than one unique number that can be put in for c, then \(a \div b\) is said to be undefined.
Instead of writing c, it is sometimes easier to write a blank or box in the equations to see if a unique solution exists. If you can put a unique solution in the blank to the multiplication problem, then you can go back and fill in the solution to the division problem.
Use the definition of division to find the answer to \(\bf 21 \div 3\).
First, note that \(21 \div 3\) = ____ means 21 = 3 \(\cdot\) _____ Second, try to fill in the blank in the multiplication problem with a unique number to make the equation, 21 = 3 \(\cdot\) _____, true: 21 = 3 \(\cdot \underline{7}\). If the number filled in is the only possible solution (unique), then that is the answer to the division problem. Therefore, \(21 \div 3\) = \(\underline{7}\). You do not need to write this paragraph for your solution. Below is how to write the solution.
Solution
Since \(21 = 3 \cdot \underline{7}\), then \( 21 \div 3 = \underline{7}\).
Use the definition of division to find the following quotients:
| a. \(32 \div 8\) |
| b. \(56 \div 8\) |
| c. \(32 \div 2\) |
| d. \(0 \div 13\) |
| e. \(12 \div 1\) |
| f. \(X \div 1\) (Assume X is any number.) |
| g. \(0 \div Y\) (Assume Y is any nonzero number. |
Exercise 25f illustrates that any number divided by 1 is itself.
In other words, \(\bf a \div 1 = a\) for all values of a.
Exercise 25g illustrates that zero divided by any nonzero whole number is 0.
In other words, \(\bf 0 \div a = 0\), for all nonzero values of a.
In the above problem, all of the answers were whole numbers. If you were asked to use the definition to find only whole number solutions, then some divisions would be undefined under whole numbers. There may, however, be rational or irrational solutions depending on the problem.
Use the definition of division to find if \(\bf 21 \div 5\) is defined under whole numbers. Show the solution if it is defined, or explain why not if it is not defined.
First, note that \(21 \div 5\) = ____ means 21 = 5 \(\cdot\) _____ Second, try to fill in the blank in the multiplication problem with a unique whole number to make the equation, 21 = 5 \(\cdot\) _____, true. There is no whole number that can be put in the blank to make that equation true. Therefore, \(21 \div 5\) is not defined under whole numbers. Here is how you would show the answer.
Solution
Since there is no whole number solution to make the equation, 21 = 5 \(\cdot\) ____ true, \( 21 \div 5\) is not defined under whole numbers.
Use the definition of division to find which of the following quotients are defined under whole numbers. Show the solution if it is defined, or explain why not if it is not defined. Part a and b are done for you. Use these as examples.
|
a. \(45 \div 5\) Solution: Since \( 45 = 5 \cdot \underline{9}\), then \(45 \div 5 = \underline{9}\). |
|
b. \(42 \div 9\) Solution: Since there is no whole number solution to make the equation, 42 = 9 \(\cdot\) ___ true, \(42 \div 9\) is not defined under whole numbers. (Yes, you should write all of this out!) |
|
c. \(48 \div 6\) Solution: |
|
d. \(35 \div 4\) Solution: |
|
e. \(48 \div 1\) Solution: |
|
f. \(55 \div 7\) Solution: |
|
g. \(0 \div 8\) Solution: |
Let's explore what happens when we divided by zero.
Use the definition of division to find the quotient: \(\bf 8 \div 0\).
First, note that \(8 \div 0\) = ____ means 8 = 0 \(\cdot\) _____ Second, try to fill in the blank in the multiplication problem with a unique number to make the equation, 8 = 0 \(\cdot\) _____, true. There is no number that can be put in the blank to make that equation true since any number times 0 is 0, and will never equal 8. This is how you could write the solution:
Solution
There is no number that will make the equation, 8 = 0 \(\cdot\) ____ true, since any number put in the blank will make the right hand side of the equation zero, which can never equal the left-hand side of the equation, which is 8. Therefore, \( 8 \div 0\) is not defined.
Use the definition of division to show that the following quotients are undefined:
a. \(6 \div 0\)
b. \(18 \div 0\)
c. \(M \div 0\) (Assume \(M \neq 0\))
In exercise 27, you showed that dividing a nonzero number by 0 was undefined. Now, let's explore what happens if we divide zero by zero.
Use the definition of division to find the quotient: \(0 \div 0\).
First, note that \(0 \div 0\) = ____ means 0 = 0 \(\cdot\) _____ Second, try to fill in the blank in the multiplication problem with a unique number to make the equation, 0 = 0 \(\cdot\) _____, true. There is no unique number that can be put in the blank to make that equation true since any number put in the blank will make the equation true, and therefore there is no unique number that will work. This is how you could write the solution:
Solution
There is no unique number that can be put in the blank to make the equation 0 = 0 \(\cdot\) ____ true, since any number will make it true. Therefore, \(0 \div 0\) is called indeterminate.
In exercise 27, you showed that a nonzero number divided by zero is undefined. The next example showed that zero divided by zero is indeterminate.
To prove that division by zero is undefined, two cases must be shown. Below is a complete proof to show that division by zero is undefined.
Problem: Prove that division by zero is undefined
Solution: The goal is to show that \(a \div 0\) is undefined for all values of a. There are two cases to consider Case 1: \(a \neq 0\); Case 2: a = 0.
Case 1: Let \(a \neq 0\). There is no unique number that could be put in the blank to make the equation, a = 0 \(\cdot\) ____, true because the left-hand side of the equation is not zero (since \(a \neq 0\)), and any number put in the blank will make the right hand side of the equation zero. Therefore, when \(a \neq 0\), \(a \div 0\) is not defined.
Case 2: Let a = 0. There is no unique number that can be put in the blank to make the equation 0 = 0 \(\cdot\) ____ true, since any number will make it true. Therefore, \(0 \div 0\) is indeterminate.
It takes practice writing this proof. You'll need to practice writing it several times to master the problem. One option is to memorize the proof shown above by writing it out a few times until you really get the idea. This would make a good exam question.
Prove that division by zero is undefined.


