22.1: How Many Groups? (Part 1)

Last updated
Save as PDF

Page ID: 40245

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Lesson

Let's play with blocks and diagrams to think about division with fractions.

Exercise $\PageIndex{1}$: Equal-Sized Groups

Write a multiplication equation and a division equation for each sentence or diagram.

Eight $5 bills are worth $40.
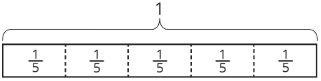
There are 9 thirds in 3 ones.

Exercise $\PageIndex{2}$: Reasoning with Pattern Blocks

Use the pattern blocks in the applet to answer the questions. (If you need help aligning the pieces, you can turn on the grid.)

If a hexagon represents 1 whole, what fraction do each of the following shapes represent? Be prepared to show or explain your reasoning.
1. 1 triangle
2. 1 rhombus
3. 1 trapezoid
4. 4 triangles
5. 3 rhombuses
6. 2 hexagons
7. 1 hexagon and 1 trapezoid
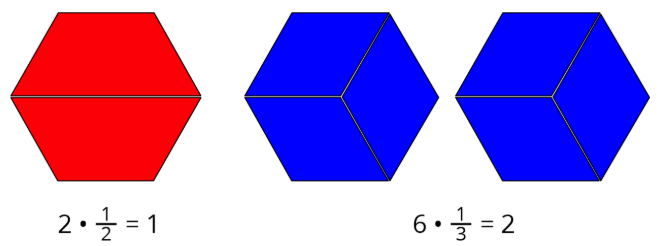
Here are Elena’s diagrams for $2\cdot\frac{1}{2}=1$ and $6\cdot\frac{1}{3}=2$. Do you think these diagrams represent the equations? Explain or show your reasoning.

Figure $\PageIndex{2}$: Two diagrams of pattern blocks: The first is of one red hexagon composed of two red trapezoids. The diagram is labeled with the equation 2 times one half equals 1. The second diagram is of two blue hexagons where each hexagon is composed of three blue rhombuses. The second diagram is labeled with the equation 6 times, one third, equals 2.

Use pattern blocks to represent each multiplication equation. Remember that a hexagon represents 1 whole.
1. $3\cdot\frac{1}{6}=\frac{1}{2}$
2. $2\cdot\frac{3}{2}=3$
Answer the questions. If you get stuck, consider using pattern blocks.
1. How many $\frac{1}{2}$s are in $4$?
2. How many $\frac{2}{3}$s are in $2$?
3. How many $\frac{1}{6}$s are in $1\frac{1}{2}$?

Summary

Some problems that involve equal-sized groups also involve fractions. Here is an example: “How many $\frac{1}{6}$ are in $2$?” We can express this question with multiplication and division equations.

$?\cdot\frac{1}{6}=2$

$2\div\frac{1}{6}=?$

Pattern-block diagrams can help us make sense of such problems. Here is a set of pattern blocks.

If the hexagon represents 1 whole, then a triangle must represent $\frac{1}{6}$, because 6 triangles make 1 hexagon. We can use the triangle to represent the $\frac{1}{6}$ in the problem.

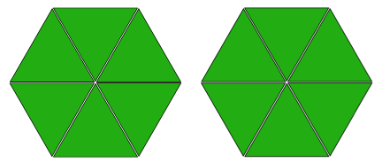
Twelve triangles make 2 hexagons, which means there are 12 groups of $\frac{1}{6}$ in 2.

If we write the 12 in the place of the “?” in the original equations, we have:

$12\cdot\frac{1}{6}=2$

$2\div\frac{1}{6}=12$

Practice

Exercise $\PageIndex{3}$

Consider the problem: A shopper buys cat food in bags of 3 lbs. Her cat eats $\frac{3}{4}$ lb each week. How many weeks does one bag last?

Draw a diagram to represent the situation and label your diagram so it can be followed by others. Answer the question.
Write a multiplication or division equation to represent the situation.
Multiply your answer in the first question (the number of weeks) by $\frac{3}{4}$. Did you get 3 as a result? If not, revise your previous work.

Exercise $\PageIndex{4}$

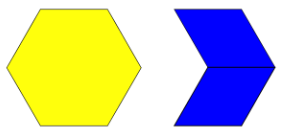
Use the diagram to answer the question: How many $\frac{1}{3}$s are in $1\frac{2}{3}$? The hexagon represents 1 whole. Explain or show your reasoning.

Exercise $\PageIndex{6}$

Write two division equations for each multiplication equation.

$15\cdot\frac{2}{5}=6$
$6\cdot\frac{4}{3}=8$
$16\cdot\frac{7}{8}=14$

Exercise $\PageIndex{7}$

Noah and his friends are going to an amusement park. The total cost of admission for 8 students is $100, and all students share the cost equally. Noah brought $13 for his ticket. Did he bring enough money to get into the park? Explain your reasoning.

(From Unit 4.1.2)

Exercise $\PageIndex{8}$

Write a division expression with a quotient that is:

greater than $8\div 0.001$
less than $8\div 0.001$
between $8\div 0.001$ and $8\div\frac{1}{10}$

(From Unit 4.1.1)

Exercise $\PageIndex{9}$

Find each unknown number.

$12$ is $150$% of what number?
$5$ is $50$% of what number?
$10$% of what number is $300$?
$5$% of what number is $72$?
$20$ is $80$% of what number?

(From Unit 3.4.5)