1.8: Logarithmic Functions

Logarithms are the inverse of exponential functions – they allow us to undo exponential functions and solve for the exponent. They are also commonly used to express quantities that vary widely in size.

Logarithm Equivalent to an Exponential

The logarithm (base \(b\)) function, written \( \log_b (x) \), is the inverse of the exponential function (base \(b\)), \( b^x \).

This means the statement \( b^a=c \) is equivalent to the statement \( \log_b (c)=a \).

Properties of Logs: Inverse Properties

• \( \log_b(b^x)=x \)
• \( b^{\log_b(x)}=x \)

Example \(\PageIndex{1}\)

Write these exponential equations as logarithmic equations:

1. \( 2^3=8 \)
2. \( 5^2=25 \)
3. \(10^{-4}=\frac{1}{10000}\)

Solution

1. \( 2^3=8 \) is equivalent to \( \log_2(8)=3 \).
2. \( 5^2=25 \) is equivalent to \( \log_5(25)=2 \).
3. \(10^{-4}=\frac{1}{10000}\) is equivalent to \( \log_{10}\left(\frac{1}{10000}\right)=-4 \).

Example \(\PageIndex{2}\)

Solve \( 2^x=10 \) for \(x\).

Solution

By rewriting this expression as a logarithm, we get \( x=\log_2(10) \).

While this does define a solution, and an exact solution at that, you may find it somewhat unsatisfying since it is difficult to compare this expression to the decimal estimate we made earlier. Also, giving an exact expression for a solution is not always useful–often we really need a decimal approximation to the solution. Luckily, this is a task calculators and computers are quite adept at. Unluckily for us, most calculators and computers will only evaluate logarithms of two bases. Happily, this ends up not being a problem, as we’ll see briefly.

Common and Natural Logarithms

The common log is the logarithm with base 10, and is typically written \( \log(x) \).

The natural log is the logarithm with base \(e\), and is typically written \( \ln(x) \).

Example \(\PageIndex{3}\)

Evaluate \( \log(1000) \) using the definition of the common log.

Solution

To evaluate \( \log(1000) \), we can say \( x=\log(1000) \), then rewrite into exponential form using the common log base of 10:\[ 10^x=1000. \nonumber \]

From this, we might recognize that 1000 is the cube of 10, so \(x = 3\).

We also can use the inverse property of logs to write \( log_{10}\left(10^3\right) =3 \).

Values of the common log

Number	Number as exponential	log(number)
1000	\( 10^3 \)	3
100	\( 10^2 \)	2
10	\( 10^1 \)	1
1	\( 10^0 \)	0
0.1	\( 10^{-1} \)	-1
0.01	\( 10^{-2} \)	-2
0.001	\( 10^{-3} \)	-3

Example \(\PageIndex{4}\)

Evaluate \( \log(500) \) using you calculator or computer.

Solution

Using a computer or calculator, we can evaluate and find that \( \log(500)\approx 2.69897 \).

Another property provides the basis for solving exponential equations.

Properties of Logs: Exponent Property

\( \log_b\left(A^r\right)=r\,\log_b(A) \)

Solving exponential equations:

1. Isolate the exponential expressions when possible.
2. Take the logarithm of both sides.
3. Utilize the exponent property for logarithms to pull the variable out of the exponent.
4. Use algebra to solve for the variable.

Example \(\PageIndex{5}\)

In the last section, we predicted the population (in billions) of India \(t\) years after 2008 by using the function \( f(t)=1.14(1+0.0134)^t \). If the population continues following this trend, when will the population reach 2 billion?

Solution

We need to solve for the \(t\) so that \(f(t) = 2\)

\(2=1.14(1.0134)^t\)	Initial equation.
\(\dfrac{2}{1.14}=1.0134^t\)	Divide by 1.14 to isolate the exponential expression.
\(\ln\left(\dfrac{2}{1.14}\right)=\ln\left(1.0134^t\right)\)	Take the logarithm of both sides of the equation.
\(\ln\left(\dfrac{2}{1.14}\right)=t\,\ln(1.0134)\)	Apply the exponent property on the right side.
\( t = \dfrac{\ln\left(\dfrac{2}{1.14}\right)}{\ln(1.0134)}\)	Divide both sides by \(\ln(1.0134)\)
\( t\approx 42.23 \text{ years} \)

If this growth rate continues, the model predicts the population of India will reach 2 billion about 42 years after 2008, or approximately in the year 2050.

Example \(\PageIndex{6}\)

Solve \( 5e^{-0.3t}=2 \) for \( t \).

Solution

First we divide by 5 to isolate the exponential: \[ e^{-0.3t}=\frac{2}{5}. \nonumber \]

Since this equation involves \(e\), it makes sense to use the natural log:

\(\ln\left(e^{-0.3t}\right)=\ln\left(\dfrac{2}{5}\right)\)	Take the natural log of both sides.
\(-0.3t=\ln\left(\dfrac{2}{5}\right)\)	Utilizing the inverse property for logs.
\( t = \dfrac{\ln\left(\dfrac{2}{5}\right)}{-0.3}\)	Now dividing by -0.3.
\( t\approx 3.054 \)

In addition to solving exponential equations, logarithmic expressions are common in many physical situations.

Example \(\PageIndex{7}\)

In chemistry, pH is a measure of the acidity or basicity of a liquid. The pH is related to the concentration of hydrogen ions, \(\left[H^+\right]\), measured in moles per liter, by the equation\[\text{pH}=-\log\left(\left[H^+\right]\right)\nonumber \]

If a liquid has concentration of 0.0001 moles per liter, determine the pH. Determine the hydrogen ion concentration of a liquid with pH of 7.

Solution

To answer the first question, we evaluate the expression \( -\log(0.0001) \). While we could use our calculators for this, we do not really need them here, since we can use the inverse property of logs: \[ -\log(0.0001)=-\log\left(10^{-4}\right)=-(-4)=4.\nonumber \]

To answer the second question, we need to solve the equation \( 7=-\log\left(\left[H^+\right]\right) \). Begin by isolating the logarithm on one side of the equation by multiplying both sides by -1: \(-7=\log\left(\left[H^+\right]\right)\). Rewriting into exponential form yields the answer: \[\left[H^+\right]=10^{-7}=0.0000001\text{ moles per liter}.\nonumber \]

While we don't often need to sketch the graph of a logarithm, it is helpful to understand the basic shape.

Graphical Features of the Logarithm

Graphically, given the function \( g(x)=\log_b(x) \).

• The graph has a horizontal intercept at (1, 0).
• The graph has a vertical asymptote at \( x = 0\).
• The graph is increasing and concave down.
• The domain of the function is \( x \gt 0\), or \( (0, \infty) \) in interval notation.
• The range of the function is all real numbers, or \( (-\infty, \infty) \) in interval notation.

When sketching a general logarithm with base \(b\), it can be helpful to remember that the graph will pass through the points \((1, 0)\) and \((b, 1)\).

To get a feeling for how the base affects the shape of the graph, examine the graphs below:

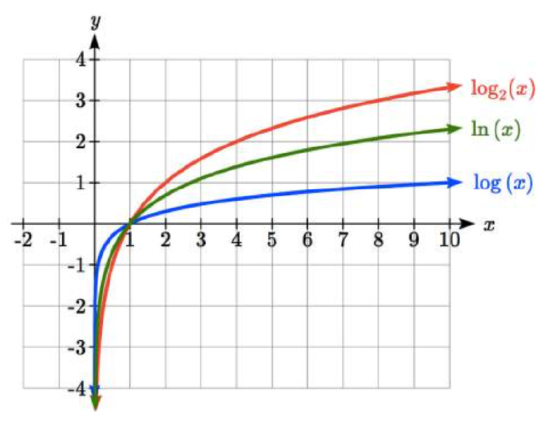
Another important observation made was the domain of the logarithm: \(x \gt 0\). Like the reciprocal and square root functions, the logarithm has a restricted domain which must be considered when finding the domain of a composition involving a log.

Example \(\PageIndex{8}\)

Find the domain of the function \( f(x)=\log(5-2x) \).

Solution

The logarithm is only defined when the input is positive, so this function will only be defined when \( 5-2x \gt 0 \). Solving this inequality, \( -2x \gt -5 \), so \( x\lt \frac{5}{2} \).

The domain of this function is \( x\lt \frac{5}{2} \), or, in interval notation, \( \left(-\infty, \frac{5}{2} \right) \).