5.6: Harder problems- finding the point of tangency

Learning Objectives

1. Find a tangent line to a function that goes through some point (not necessarily on the graph of the function).
2. Determine tangent lines to functions that contain unspecified parameters.

In this section, we present a sample of problems in which the path to a solution is more subtle. In some of these, finding the point of tangency is part of the question. We must use clues about the function to solve for that point, as well as construct the tangent line equation from information supplied. In other cases, the problem involves a parameter whose value is not specified initially. Such examples are meant to hone problem solving skills.

Example 5.13

Find any value(s) of the constant a such that the line \(y=a x\) is tangent to the curve \(y=f(x)=-x^{2}+3 x-2\).

Solution

Figure 5.10: Figure for Example 5.13: finding the point of tangency.

We do not know the coordinate of any such point, but we label it \(x_{0}\) in Figure \(5.10\) to denote that it is a definite (as yet to be determined) value. Finding \(x_{0}\) is part of the problem. We collect the information to be used:

• The tangent line \(y=a x\) intersects the graph of the function \(y=f(x)=\) \(-x^{2}+3 x-2\) at \(\left(x_{0}, f\left(x_{0}\right)\right)\).
• Equating \(y\) values of the tangent line and the curve \(y=f(x)\) at \(x_{0}\) we get: \[f\left(x_{0}\right)=-x_{0}^{2}+3 x_{0}-2=a x_{0} . \nonumber \]
• The equation of the tangent line is \(y=a x\). Its slope is \(a\), which is also the derivative of \(f(x)\) at \(x_{0}\). Equating slopes gives:

\[f^{\prime}\left(x_{0}\right)=-2 x_{0}+3=a . \nonumber \]

We have two equations with two unknowns, \(\left(a\right.\) and \(\left.x_{0}\right)\). We can solve this system by substituting the value of \(a\) from the first equation into the second, getting

\[-x_{0}^{2}+3 x_{0}-2=\left(-2 x_{0}+3\right) x_{0} . \nonumber \]

Simplifying:

\[-x_{0}^{2}+3 x_{0}-2=-2 x_{0}^{2}+3 x_{0} \quad \Rightarrow \quad x_{0}^{2}-2=0, \quad x_{0}=\pm \sqrt{2} . \nonumber \]

Thus, there are two possible points of tangency, as shown in Figure 5.11.

Figure 5.11: Two points of tangency in the solution to Example 5.13

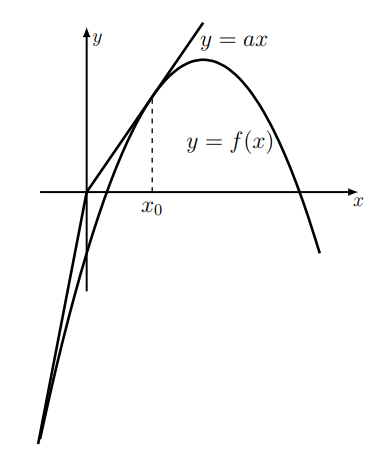
Finally, we find \(a\) using \(a=-2 x_{0}+3\). We get:

\(x_{0}=\sqrt{2} \Rightarrow a=-2 \sqrt{2}+3, \quad\) and \(\quad x_{0}=-\sqrt{2} \quad \Rightarrow \quad a=2 \sqrt{2}+3\).

The solution to Example 5.13 was set up by

• listing of information provided,
• deducing a set of equations based on that information, and
• following a chain of reasoning to arrive at the final solution.

Practicing such multi-step problems is a critical part of training for many fields, including science, medicine, engineering, etc.

Mastered Material Check

18. Factor \(f(x)=-x^{2}+3 x-2\). Does the shape depicted in Figure 5.10 make sense?

Example 5.14

Find the equation of the tangent line to the curve \(y=f(x)=\) \(1-x^{2}\) that goes through the point \((1,1)\).

Solution

Finding the point of tangency \(x_{0}\) is part of the problem. We use the following facts:

• The tangent line goes through the point \(\left(x_{0}, f\left(x_{0}\right)\right)\) on the graph of the function and has slope \(f^{\prime}\left(x_{0}\right)\).
• Consequently, its equation has the form Equation (5.2): \(y=f\left(x_{0}\right)=f^{\prime}\left(x_{0}\right)(x-\) \(\left.x_{0}\right)\).

For the given function and point of tangency \(x_{0}\), we have

\[f\left(x_{0}\right)=1-x_{0}^{2}, \quad f^{\prime}\left(x_{0}\right)=-2 x_{0} . \nonumber \]

Hence the tangent line equation is

\[y=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)=\left(1-x_{0}^{2}\right)-2 x_{0}\left(x-x_{0}\right) . \nonumber \]

We are told that this line goes through the point \((x, y)=(1,1)\) so that

\[1=\left(1-x_{0}^{2}\right)-2 x_{0}\left(1-x_{0}\right), \quad \Rightarrow 0=x_{0}^{2}-2 x_{0}, \quad \Rightarrow \quad x_{0}^{2}=2 x_{0} . \nonumber \]

Thus, there are two possible points of tangency, \(x_{0}=0,2\) and two tangent lines that satisfy the given condition. Plugging in these two values of \(x_0\) into the generic equation for \(y\) leads to the two tangent line equations

1. \(y=1\), and
2. \(y=\left(1-2^{2}\right)-2 \cdot 2(x-2)=-3-4(x-2)\).

We can also find points of tangency for functions that contain general constants, as the next example illustrates.

Mastered Material Check

19. Identify the slope of the line \(y=\left(1-x_{0}^{2}\right)-2 x_{0}\left(x-x_{0}\right)\).
20. Determine the \(y\)-intercept of the line \(y=\left(1-x_{0}^{2}\right)-2 x_{0}\left(x-x_{0}\right)\).
21. Check that both lines found as solutions to Example \(5.14\) go through \((1,1)\) as desired.

Example 5.12

Shown in Figure \(5.12\) is the function \[f(x)=C \frac{x}{x+a} \nonumber \] together with one of its tangent lines. The tangent line goes through a point \((-d, 0)\). Find the equation of the tangent line.

Solution

Finding the point of tangency \(x_{0}\) is part of the problem in this case too. We use the same approach, and employ facts (1) and (2) from Example 5.14. We also use, for the specific function in this example,

\[f\left(x_{0}\right)=C \frac{x_{0}}{x_{0}+a} \quad \Rightarrow \quad f^{\prime}\left(x_{0}\right)=C \frac{a}{\left(x_{0}+a\right)^{2}} . \nonumber \]

(See Exercise 10 in Chapter 3). Hence, the equation of the tangent line is

\[y=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)=C \frac{x_{0}}{x_{0}+a}+C \frac{a}{\left(x_{0}+a\right)^{2}}\left(x-x_{0}\right) . \nonumber \]

We can simplify this equation by factoring to obtain:

\[y=\frac{C}{\left(x_{0}+a\right)^{2}}\left(x_{0}\left(x_{0}+a\right)+a\left(x-x_{0}\right)\right)=\frac{C}{\left(x_{0}+a\right)^{2}}\left(x_{0}^{2}+a x\right) . \nonumber \]

Figure 5.12: The graph of a function and its tangent line for Example 5.15.

It is important to realize that in this equation, \(x_{0}, C\) and \(a\) represent fixed (known) constants, and only \(x, y\) are variables. This means that the equation expresses a linear relationship between \(x\) and \(y\), as appropriate for a straight line.

We know that the point \((-d, 0)\) is on this line, so that (plugging in \(x=\) \(-d, y=0\) ), we obtain

\[0=\frac{C}{\left(x_{0}+a\right)^{2}}\left(x_{0}^{2}-a d\right) . \nonumber \]

Solving for \(x_{0}\) leads to \(x_{0}=\sqrt{a d}\). Moreover, we can now find the equation of the tangent line in terms of these parameters.

\[y=\frac{C}{(\sqrt{a d}+a)^{2}}(a d+a x) \quad \Rightarrow \quad y=\frac{C}{(\sqrt{(d / a)}+1)^{2}}(d+x) \nonumber \]

where we have simplified by factoring \(a\) from numerator and denominator. We can easily see that when \(x=-d\), we get \(y=0\), as required. This forms one check that our calculations are correct.