10.5: Inverses

Suppose \(f: A\rightarrow B\) is a function. By definition, \(f\) associates an element of \(B\) to each element of \(A\text{.}\) Sometimes we want to reverse this process: given an element \(b \in B\text{,}\) can we determine an element \(a \in A\) such that \(f(a) = b\text{?}\) We'll begin to answer this question by first finding all possible “reverse results” from elements in subsets of \(B\text{.}\)

Definition: inverse image (of a subset \(C\) of the codomain \(B\))

the set of all domain elements \(a \in A\) for function \(f: A\rightarrow B\) for which the corresponding output element \(f(a)\) lies in the subset \(C\) of the codomain

Definition: \(f^{-1}(C)\)

the inverse image of the subset \(C \subseteq B\) under the function \(f: A\rightarrow B\text{,}\) so that

\begin{equation*} f^{-1}(C) = \{a \in A \vert f(a) \in C\} \end{equation*}

Figure \(\PageIndex{1}\): A Venn diagram of a function inverse image.

Idea \(\PageIndex{1}\)

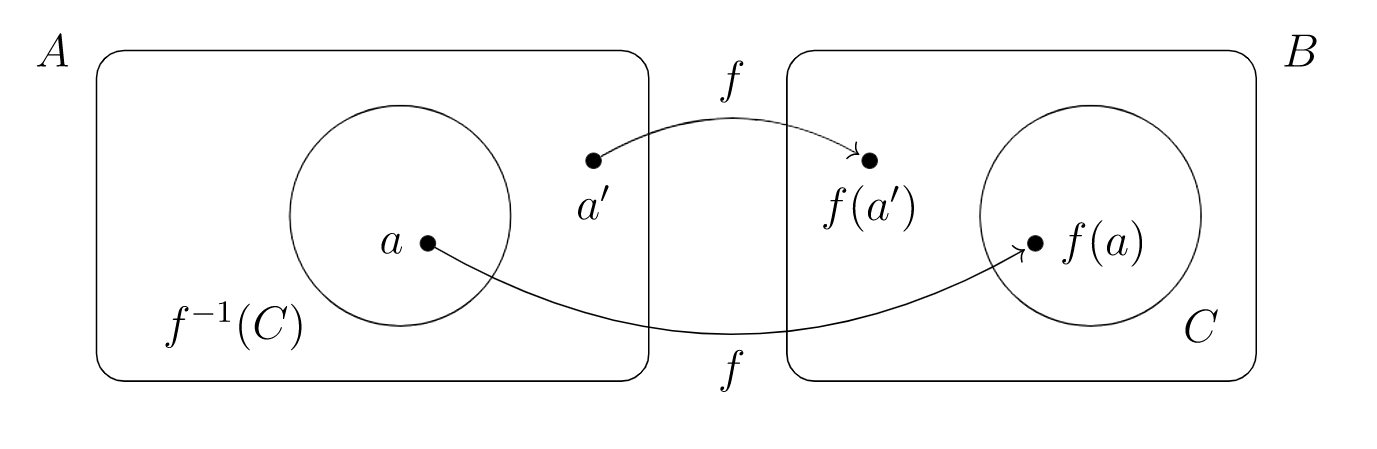
As in the figure above, \(f^{-1}(C)\) collects together all those elements of \(A\) whose images under \(f\) land inside \(C\text{.}\)

Example \(\PageIndex{1}\): Some inverse images under sine.

Consider \(f: \mathbb{R} \rightarrow \mathbb{R}\text{,}\) \(f(x) = \sin x\text{.}\)

Then

\begin{equation*} f^{-1}(\{-1,0,1\}) = \left \{\dfrac{m \pi}{2} \vert m \in \mathbb{Z} \right \} \end{equation*}
because

\begin{equation*} \sin\left(\dfrac{m \pi}{2}\right) \end{equation*}
will equal \(0\) when \(m\) is even and will equal \(1\) or \(-1\) when \(m\) is odd, and no other input values will produce outputs of \(0\text{,}\) \(1\text{,}\) or \(-1\text{.}\)

However,

\begin{equation*} f^{-1}(\{y \in \mathbb{R} \rightarrow y \gt 1\}) = \emptyset \end{equation*}
because there are no input values for sine that will produce an output value greater than \(1\text{.}\)

Now let's return to the question of trying to reverse an input-output relationship \(f(a) = b\text{:}\) the set \(f^{-1}\bbrac{\{b\}}\) collects together all possible candidates for the inverse image of \(b\text{.}\)

Definition: inverse image (of an element \(b\) of the codomain \(B\))

the inverse image \(f^{-1}(\{b\})\text{,}\) which consists of all domain elements \(a \in A\) for which \(f(a) = b\)

Definition: \(f^{-1} (b)\)

simplified notation to mean the inverse image of element \(b\)

This gives us a way to associate to an element \(b \in B\) a set \(f^{-1} (b)\) of elements of \(A\text{.}\)

Question \(\PageIndex{1}\)

When does this association \(b \mapsto f^{-1} (b)\) give us a function \(f^{-1} : B \rightarrow A\text{?}\)

There are two possible ways that this will fail to give us a function.

1. Suppose there is an element \(b \in B\) such that the set \(f^{-1} (b)\) contains (at least) two distinct elements \(a_1,a_2\text{.}\) Then in general there is no way to choose between \(f^{-1} (b) = a_1\) and \(f^{-1} (b) = a_2\text{.}\) Therefore, if \(f\) is not injective, the function \(f^{-1} : B \rightarrow A\) is not well-defined.
2. Suppose there is an element \(b \in B\) such that \(f^{-1} (b) = \emptyset \text{.}\) Then there is no element of \(A\) which we can assign to \(f^{-1} (b)\text{.}\) Therefore, if \(f\) is not surjective, the function \(f^{-1} : B \rightarrow A\) is undefined on some elements of \(B\text{.}\)

So it seems we will need a function to be bijective in order to be able to reverse the input-output rule to obtain an inverse function.

Definition: inverse function

for a bijective function \(f\text{,}\) the inverse function associates to each codomain element of \(f\) the corresponding unique domain element that produces it through \(f\)

Definition: \(f^{-1}\)

the inverse function \(f^{-1} : B \rightarrow A\) for bijective function \(f: A\rightarrow B\text{,}\) so that for \(b \in B\) we have \(f^{-1} (b)\) defined to be the unique element \(a \in A\) such that \(f(a) = b\)

Example \(\PageIndex{2}\): An invertible single-variable, real-valued function

The function \(f: \mathbb{R} \rightarrow \mathbb{R}\text{,}\) \(f(x) = x^3\text{,}\) is bijective and has inverse \(f^{-1}(x) = x^{\dfrac{1}{3}}\text{.}\)

Example \(\PageIndex{3}\): Inverting a numerical encoding of the alphabet

Returning again to the bijection \(\varphi: \Sigma \rightarrow B\) encountered in Example 10.2.4 and Example 10.2.6, where

\begin{align*} \Sigma & = \{a, b, \ldots, z\} , & B & = \{ 1, 2, \ldots, 26 \}, \end{align*}
the inverse function \(\varphi ^{-1} : B \rightarrow \Sigma\) associates to each number \(1 \le b \le 26\) the corresponding letter at that position of the alphabet. For example, \(\varphi^{-1} (11) = \text{k} \text{.}\)

Example \(\PageIndex{4}\): A non-invertible function

The function \(g:\mathbb{R} \rightarrow \mathbb{R}\text{,}\) \(g(x) = x^2\text{,}\) does not have an inverse since it is not bijective. However, the function \(h:\mathbb{R}_{\geq 0}: \mathbb{R}_{\geq 0}\text{,}\) \(h(x) = x^2\text{,}\) so that \(h = g\vert _{\mathbb{R}_{\geq 0}}\) but with codomain also restricted down to the image of \(g\text{,}\) has inverse \(h^{-1}(x) = \sqrt{x}\text{.}\)

Note

If \(f\) is bijective, then so is \(f^{-1}\text{,}\) and \(f^{-1}\) is the unique function \(B \to A\) such that both

\begin{align*} f^{-1} \circ f & = \id_A, & f \circ f^{-1} & = \id_B \text{.} \end{align*}

Checkpoint

Prove that if \(f\) is bijective then so is \(f^{-1}\text{,}\) and \((f^{-1})^{-1} = f\text{.}\)