3.5: Solution of the Heat Equation
- Page ID
- 90928
We started this chapter seeking solutions of initial-boundary value problems involving the heat equation and the wave equation. In particular, we found the general solution for the problem of heat flow in a one dimensional rod of length \(L\) with fixed zero temperature ends. The problem was given by
\[\begin{array}{ccc} \text { PDE } & u_{t}=k u_{x x}, & 0<t, \quad 0 \leq x \leq L, \\ \text { IC } & u(x, 0)=f(x), & 0<x<L, \\ \text { BC } & u(0, t)=0, & t>0, \\ & u(L, t)=0, & t>0 . \end{array}\label{eq:1} \]
We found the solution using separation of variables. This resulted in a sum over various product solutions: \[u(x, t)=\sum_{n=1}^{\infty} b_{n} e^{k \lambda_{n} t} \sin \frac{n \pi x}{L},\nonumber \] where \[\lambda_{n}=-\left(\frac{n \pi}{L}\right)^{2} .\nonumber \]
This equation satisfies the boundary conditions. However, we had only gotten to state initial condition using this solution. Namely, \[f(x)=u(x, 0)=\sum_{n=1}^{\infty} b_{n} \sin \frac{n \pi x}{L} .\nonumber \] We were left with having to determine the constants \(b_{n}\). Once we know them, we have the solution.
Now we can get the Fourier coefficients when we are given the initial condition, \(f(x)\). They are given by \[b_{n}=\frac{2}{L} \int_{0}^{L} f(x) \sin \frac{n \pi x}{L} d x, \quad n=1,2, \ldots .\nonumber \]
We consider a couple of examples with different initial conditions.
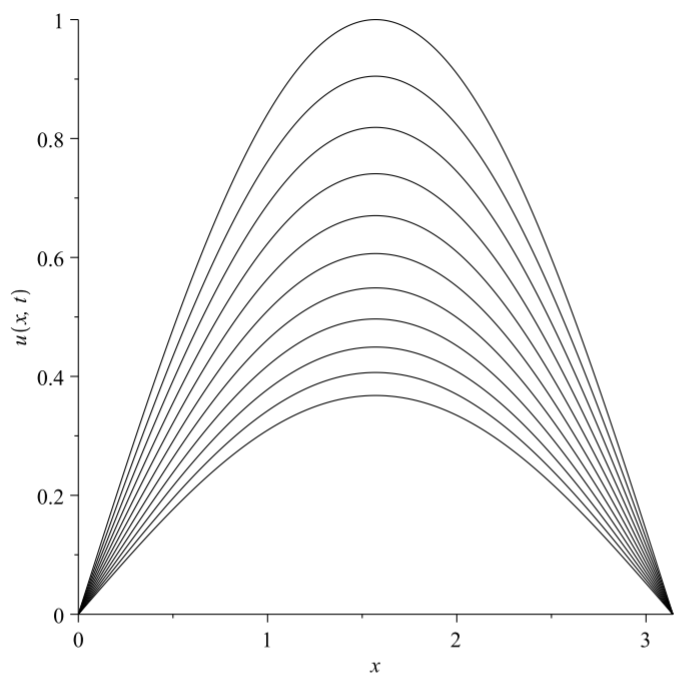
Consider the solution of the heat equation with \(f(x)=\sin x\) and \(L=\pi\).
In this case the solution takes the form \[u(x, t)=\sum_{n=1}^{\infty} b_{n} e^{k \lambda_{n} t} \sin n x .\nonumber \]
However, the initial condition takes the form of the first term in the expansion; i.e., the \(n=1\) term. So, we need not carry out the integral because we can immediately write \(b_{1}=1\) and \(b_{n}=0, n=2,3, \ldots\). Therefore, the solution consists of just one term, \[u(x, t)=e^{-k t} \sin x .\nonumber \]
In Figure \(\PageIndex{1}\) we see that how this solution behaves for \(k=1\) and \(t \in[0,1]\).
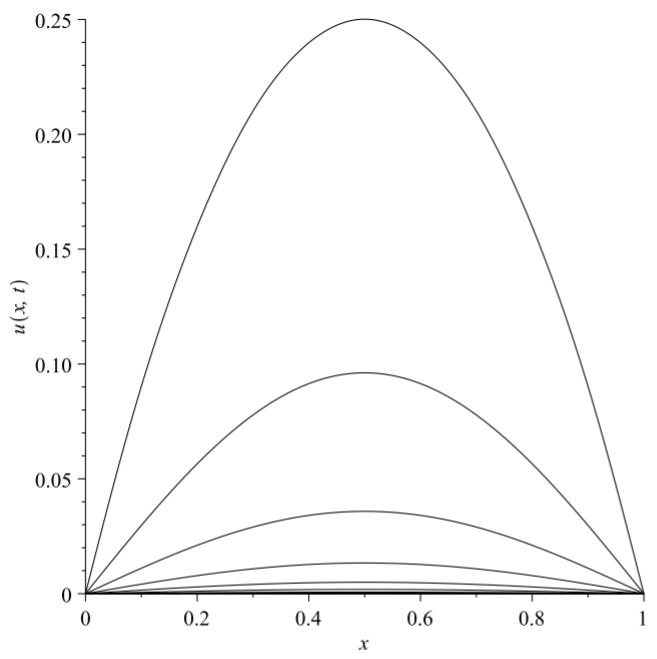
Consider solutions of the heat equation with \(f(x) = x(1 − x)\) and \(L = 1\).
This example requires a bit more work. The solution takes the form \[u(x,t)=\sum\limits_{n=1}^\infty b_ne^{-n^2\pi^2kt}\sin n\pi x,\nonumber\] where \[b_n=2\int_0^1 f(x)\sin n\pi xdx.\nonumber\] This integral is easily computed using integration by parts \[\begin{align} b_n&=2\int_0^1 x(1-x)\sin n\pi xdx\nonumber \\ &=\left[2x(1-x)\left(-\frac{1}{n\pi}\cos n\pi x\right)\right]_0^1+\frac{2}{n\pi}\int_0^1(1-2x)\cos n\pi xdx \nonumber \\ &=-\frac{2}{n^2\pi^2}\left\{ [(1-2x)\sin n\pi x]_0^1+2\int_0^1\sin n\pi xdx\right\}\nonumber \\ &=\frac{4}{n^3\pi^3}[\cos n\pi x]_0^1\nonumber \\ &=\frac{4}{n^3\pi^3}(\cos n\pi -1) \nonumber \\ &=\left\{\begin{array}{cl} 0,&n\text{ even} \\ -\frac{8}{n^3\pi^3}&n\text{ odd}\end{array}\right.\label{eq:2} \end{align}\]
So, we have that the solution can be written as \[u(x,t)=\frac{8}{\pi^3}\sum\limits_{\ell =1}^\infty\frac{1}{(2\ell -1)^3}e^{-(2\ell -1)^2\pi^2kt}\sin (2\ell -1)\pi x.\nonumber\]
In Figure \(\PageIndex{2}\) we see that how this solution behaves for \(k=1\) and \(t \in[0,1]\). Twenty terms were used. We see that this solution diffuses much faster than in the last example. Most of the terms damp out quickly as the solution asymptotically approaches the first term.