8.4: Complex Differentiation

Next we want to differentiate complex functions. We generalize the definition from single variable calculus, \[f^{\prime}(z)=\lim _{\Delta z \rightarrow 0} \frac{f(z+\Delta z)-f(z)}{\Delta z},\label{eq:1}\] provided this limit exists.

The computation of this limit is similar to what one sees in multivariable calculus for limits of real functions of two variables. Letting \(z=x+i y\) and \(\delta z=\delta x+i \delta y\), then \[z+\delta x=(x+\delta x)+i(y+\delta y)\nonumber \] Letting \(\Delta z \rightarrow 0\) means that we get closer to \(z\). There are many paths that one can take that will approach \(z\). [See Figure \(\PageIndex{1}\).]

Figure \(\PageIndex{1}\): There are many paths that approach \(z\) as \(\Delta z \rightarrow 0\).

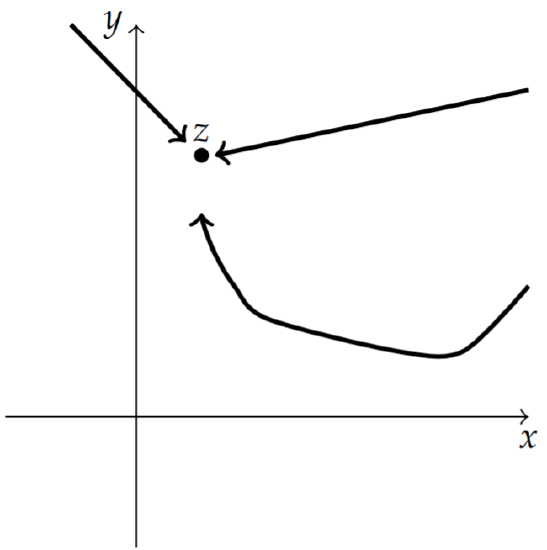
It is sufficient to look at two paths in particular. We first consider the path \(y=\) constant. This horizontal path is shown in Figure \(\PageIndex{2}\). For this path, \(\Delta z=\Delta x+i \Delta y=\Delta x\), since \(y\) does not change along the path. The derivative, if it exists, is then computed as \[\begin{align} f^{\prime}(z) &=\lim _{\Delta z \rightarrow 0} \frac{f(z+\Delta z)-f(z)}{\Delta z}\nonumber \\ &=\lim _{\Delta x \rightarrow 0} \frac{u(x+\Delta x, y)+i v(x+\Delta x, y)-(u(x, y)+i v(x, y))}{\Delta x}\nonumber \\ &=\lim _{\Delta x \rightarrow 0} \frac{u(x+\Delta x, y)-u(x, y)}{\Delta x}+\lim _{\Delta x \rightarrow 0} i \frac{v(x+\Delta x, y)-v(x, y)}{\Delta x}\label{eq:2} \end{align}\] The last two limits are easily identified as partial derivatives of real valued functions of two variables. Thus, we have shown that when \(f^{\prime}(z)\) exists, \[f^{\prime}(z)=\frac{\partial u}{\partial x}+i \frac{\partial v}{\partial x}\label{eq:3}\]

Figure \(\PageIndex{2}\): A path that approaches \(z\) with \(y=\) constant.

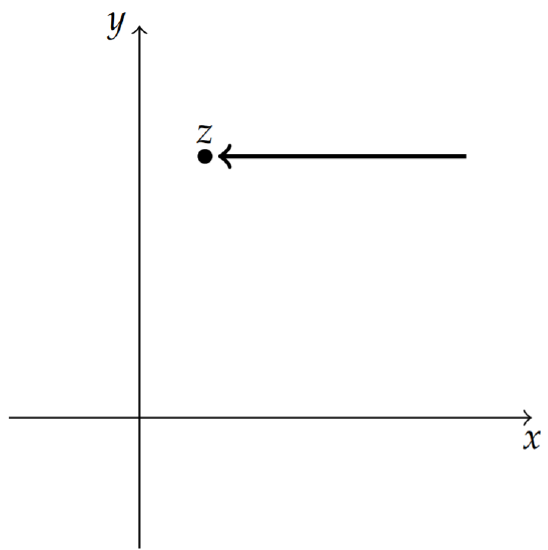
A similar computation can be made if instead we take the vertical path, \(x=\) constant, in Figure \(\PageIndex{1}\)). In this case \(\Delta z=i \Delta y\) and \[\begin{align} f^{\prime}(z) &=\lim _{\Delta z \rightarrow 0} \frac{f(z+\Delta z)-f(z)}{\Delta z}\nonumber \\ &=\lim _{\Delta y \rightarrow 0} \frac{u(x, y+\Delta y)+i v(x, y+\Delta y)-(u(x, y)+i v(x, y))}{i \Delta y}\nonumber \\ &=\lim _{\Delta y \rightarrow 0} \frac{u(x, y+\Delta y)-u(x, y)}{i \Delta y}+\lim _{\Delta y \rightarrow 0} \frac{v(x, y+\Delta y)-v(x, y)}{\Delta y}\label{eq:4} \end{align}\]

Therefore, \[f'(z)=\frac{\partial v}{\partial y}-i\frac{\partial u}{\partial y}.\label{eq:5}\]

We have found two different expressions for \(f^{\prime}(z)\) by following two different paths to \(z\). If the derivative exists, then these two expressions must be the same. Equating the real and imaginary parts of these expressions, we have \[\begin{align} \frac{\partial u}{\partial x}&=\frac{\partial v}{\partial y}\nonumber \\ \frac{\partial v}{\partial x}&=-\frac{\partial u}{\partial y}\label{eq:6} \end{align}\]

These are known as the Cauchy-Riemann equations\(^{1}\).

Note

Augustin-Louis Cauchy \((1789-1857)\) was a French mathematician well known for his work in analysis. Georg Friedrich Bernhard Riemann \((1826-1866)\) was a German mathematician who made major contributions to geometry and analysis.

Theorem \(\PageIndex{1}\)

\(f(z)\) is holomorphic (differentiable) if and only if the Cauchy-Riemann equations are satisfied.

Example \(\PageIndex{1}\)

\(f(z)=z^{2}\).

Solution

In this case we have already seen that \(z^{2}=x^{2}-y^{2}+2 i x y\). Therefore, \(u(x, y)=\) \(x^{2}-y^{2}\) and \(v(x, y)=2 x y\). We first check the Cauchy-Riemann equations. \[\begin{align} \frac{\partial u}{\partial x}=2 x&=\frac{\partial v}{\partial y}\nonumber \\ \frac{\partial v}{\partial x}=2 y&=-\frac{\partial u}{\partial y} .\label{eq:7} \end{align}\] Therefore, \(f(z)=z^{2}\) is differentiable.

We can further compute the derivative using either Equation \(\eqref{eq:3}\) or Equation \(\eqref{eq:5}\). Thus, \[f^{\prime}(z)=\frac{\partial u}{\partial x}+i \frac{\partial v}{\partial x}=2 x+i(2 y)=2 z .\nonumber \] This result is not surprising.

Example \(\PageIndex{2}\)

\(f(z)=\bar{z}\).

Solution

In this case we have \(f(z)=x-i y\). Therefore, \(u(x, y)=x\) and \(v(x, y)=-y\). But, \(\frac{\partial u}{\partial x}=1\) and \(\frac{\partial v}{\partial y}=-1\). Thus, the Cauchy-Riemann equations are not satisfied and we conclude the \(f(z)=\bar{z}\) is not differentiable.

Note

Harmonic functions satisfy Laplace’s equation.

Another consequence of the Cauchy-Riemann equations is that both \(u(x, y)\) and \(v(x, y)\) are harmonic functions. A real-valued function \(u(x, y)\) is harmonic if it satisfies Laplace’s equation in \(2 \mathrm{D}, \nabla^{2} u=0\), or \[\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}=0 \text {. }\nonumber \]

Theorem \(\PageIndex{1}\)

\(f(z)=u(x, y)+i v(x, y)\) is differentiable if and only if \(u\) and \(v\) are harmonic functions.

This is easily proven using the Cauchy-Riemann equations.

\[\begin{align} \frac{\partial^{2} u}{\partial x^{2}} &=\frac{\partial}{\partial x} \frac{\partial u}{\partial x}\nonumber \\ &=\frac{\partial}{\partial x} \frac{\partial v}{\partial y} \nonumber \\ &=\frac{\partial}{\partial y} \frac{\partial v}{\partial x}\nonumber \\ &=-\frac{\partial}{\partial y} \frac{\partial u}{\partial y}\nonumber \\ &=-\frac{\partial^{2} u}{\partial y^{2}}\label{eq:8} \end{align}\]

Example \(\PageIndex{3}\)

Is \(u(x, y)=x^{2}+y^{2}\) harmonic?

Solution

\[\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}=2+2 \neq 0 .\nonumber \] No, it is not.

Example \(\PageIndex{4}\)

Is \(u(x, y)=x^{2}-y^{2}\) harmonic?

Solution

\[\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}=2-2=0 \text {. }\nonumber \] Yes, it is.

Given a harmonic function \(u(x, y)\), can one find a function, \(v(x, y)\), such The harmonic conjugate function. \(f(z)=u(x, y)+i v(x, y)\) is differentiable? In this case, \(v\) are called the harmonic conjugate of \(u\).

Example \(\PageIndex{5}\)

Find the harmonic conjugate of \(u(x, y)=x^{2}-y^{2}\) and determine \(f(z)=u+i v\) such that \(u+i v\) is differentiable.

Solution

The Cauchy-Riemann equations tell us the following about the unknown function, \(v(x, y)\) : \[\begin{gathered} \frac{\partial v}{\partial x}=-\frac{\partial u}{\partial y}=2 y, \\ \frac{\partial v}{\partial y}=\frac{\partial u}{\partial x}=2 x . \end{gathered}\nonumber \]

We can integrate the first of these equations to obtain \[v(x, y)=\int 2 y d x=2 x y+c(y) \text {. }\nonumber \] Here \(c(y)\) is an arbitrary function of \(y\). One can check to see that this works by simply differentiating the result with respect to \(x\).

However, the second equation must also hold. So, we differentiate the result with respect to \(y\) to find that \[\frac{\partial v}{\partial y}=2 x+c^{\prime}(y) \text {. }\nonumber \] Since we were supposed to get \(2 x\), we have that \(c^{\prime}(y)=0\). Thus, \(c(y)=k\) is a constant.

We have just shown that we get an infinite number of functions, \[v(x, y)=2 x y+k,\nonumber \] such that \[f(z)=x^{2}-y^{2}+i(2 x y+k)\nonumber \] is differentiable. In fact, for \(k=0\) this is nothing other than \(f(z)=z^{2}\).