8.7: More exercises

Exercise $\PageIndex{1}$

Assume that an angle bisector of a nondegenerate triangle bisects the opposite side. Show that the triangle is isosceles.

Hint

Apply Lemma 8.4.1. Also see the solution of Exercise 11.1.1.

Exercise $\PageIndex{2}$

Assume that at one vertex of a nondegenerate triangle the bisector coincides with the altitude. Show that the triangle is isosceles.

Hint

Apply ASA to the two triangles that the bisector cuts from the original triangle.

Exercise $\PageIndex{3}$

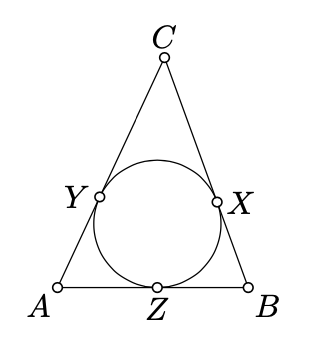
Assume sides $[BC]$, $[CA]$, and $[AB]$ of $\triangle ABC$ are tangent to the incircle at $X$, $Y$, and $Z$ respectively. Show that

$AY = AZ = \dfrac{1}{2} \cdot (AB + AC - BC).$

By the definition, the vertexes of orthic triangle are the base points of the altitudes of the given triangle.

Hint

Let $I$ be the incenter. By SAS, we get that $\triangle AIZ \cong \triangle AIY$. Therefore, $AY = AZ$. The same way we get that $BX = BZ$ and $CX = CY$. Hence the result.

Exercise $\PageIndex{4}$

Prove that the orthocenter of an acute triangle coincides with the incenter of its orthic triangle.

What should be an analog of this statement for an obtuse triangle?

Hint

Let $\triangle ABC$ be the given acute triangle and $\triangle A'B'C'$ be its orthic triangle. Note that $\triangle AA'C \sim \triangle BB'C$. Use it to show that $\triangle A'B'C \sim \triangle ABC$.

The same way we get that $\triangle AB'C' \sim \triangle ABC$. It follows that $\measuredangle A'B'C = \measuredangle AB'C'$. Conclude that $(BB')$ bisects $\angle A'B'C'$.

If $\triangle ABC$ is obtuse, then its orthocenter coincides with one of the excenters of $\triangle ABC$; that is, the point of intersection of two external and one internal bisectors of $\triangle ABC$.

Exercise $\PageIndex{5}$

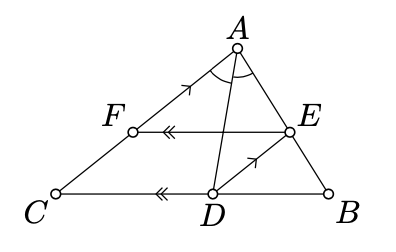
Assume that the bisector at $A$ of the triangle $ABC$ intersects the side $[BC]$ at the point $D$; the line thru $D$ and parallel to $(CA)$ intersects $(AB)$ at the point $E$; the line thru $E$ and parallel to $(BC)$ intersects $(AC)$ at $F$. Show that $AE = FC$.

Hint

Apply Theorem 4.3.1, Theorem 7.3.1 and Lemma 7.5.1.