7.2: Reflection Across a Point
- Page ID
- 23620
Fix a point \(O\). If \(O\) is the midpoint of a line segment \([XX']\), then we say that \(X'\) is a reflection of \(X\) across the point \(O\).
Note that the map \(X \mapsto X'\) is uniquely defined; it is called a reflection across \(O\). In this case \(O\) is called the center of reflection. We assume that \(O' = O\); that is, \(O\) is a reflection of itself across itself. If the reflection across \(O\) moves a set \(S\) to itself, then we say that \(S\) is centrally symmetric with respect to \(O\).
Recall that any motion is either direct or indirect; that is, it either preserves or reverts the signs of angles.
Any reflection across a point is a direct motion.
- Proof
-
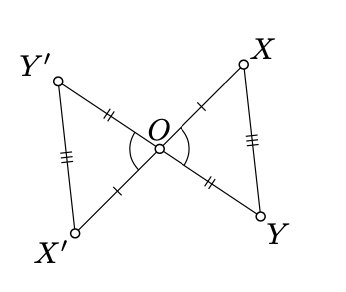
Observe that if \(X'\) is a reflection of \(X\) acroos \(O\), then \(X\) is a reflection of \(X'\). In other words, the composition of the reflection with itself is the identity map. In particular, any reflection across a point is a bijection.
Fix two points \(X\) and \(Y\); let \(X'\) and \(Y'\) be their reflection across \(O\). To check that the reflection is distance preserving, we need to show that \(X'Y' = XY\).
We may assume that \(X, Y\) and \(O\) are distinct; otherwise the statement is trivial. By definition of reflection across \(O\), we have that \(OX = OX'\), \(OY = OY'\), and the angles \(XOY\) and \(X'OY'\) are vertical; in particular \(\measuredangle XOY = \measuredangle X'OY'\). By SAS, \(\triangle XOY \cong \triangle X'OY'\); therefore \(X'Y' = XY\).
Finally, the reflection across \(O\) cannot be indirect since \(\measuredangle XOY = \measuredangle X'OY'\); therefore it is a direct motion.
Suppose \(\angle AOB\) is right. Show that the composition of reflections across the lines \((OA)\) and \((OB)\) is a reflection across \(O\).
Use this statement and Corollary 5.4.1 to build another proof of Proposition \(\PageIndex{1}\).
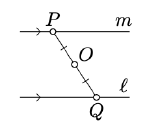
Let \(\ell\) be a line, \(Q \in \ell\), and \(P\) is an arbitrary point. Suppose \(O\) is the midpoint of \([PQ]\). Then a line \(m\) passing thru \(P\) is parallel to \(\ell\) if and only if \(m\) is a reflection of \(\ell\) across \(O\).
- Proof
-
"if" part. Assume \(m\) is a reflection of \(\ell\) across \(O\). Suppose \(\ell \nparallel m\); that is \(\ell\) and \(m\) intersect at a single point \(Z\). Denote by \(Z'\) be the reflection of \(Z\) across \(O\).

Note that \(Z'\) lies on both lines \(\ell\) and \(m\). It follows that \(Z' = Z\) or equivalently \(Z = O\). In this case \(O \in \ell\) and therefore the reflection of \(\ell\) across \(O\) is \(\ell\) itself; that is, \(\ell = m\) and in particular \(\ell \parallel m\) -- a contradiction.
"Only-if" part. Let \(\ell '\) be the reflection of \(\ell\) across \(O\). According to the "if" part of the theorem, \(\ell ' \parallel \ell\). Note that both lines \(\ell '\) and \(m\) pass thru \(P\). By uniqueness of parallel lines (Theorem 7.1.1), if \(m \parallel \ell\), then \(\ell ' = m\); whence the statement follows.


