5.3.1: Exercises 5.3
( \newcommand{\kernel}{\mathrm{null}\,}\)
In Exercises 5.3.1.1 – 5.3.1.4, vectors →x and →y are given. Sketch →x, →y, →x+→y, and →x−→y on the same Cartesian axes.
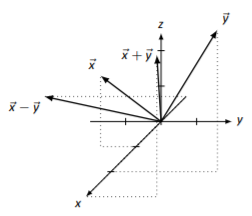
→x=[1−12],→y=[232]
- Answer
-
→x+→y=[324],→x−→y=[−1−40]
Sketches will vary slightly depending on orientation.
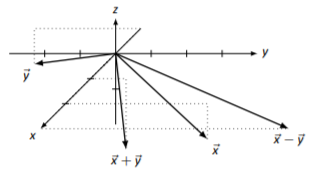
→x=[24−1],→y=[−1−3−1]
- Answer
-
→x+→y=[11−2],→x−→y=[370]
Sketches will vary slightly depending on orientation.
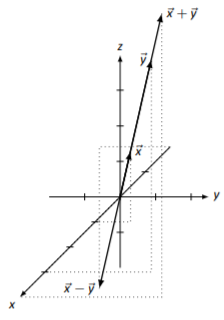
→x=[112],→y=[336]
- Answer
-
→x+→y=[448],→x−→y=[−2−2−4]
Sketches will vary slightly depending on orientation.
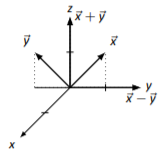
→x=[011],→y=[0−11]
- Answer
-
→x+→y=[002],→x−→y=[020]
Sketches may vary slightly.
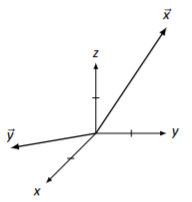
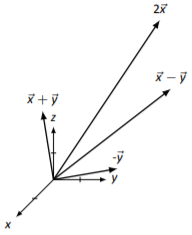
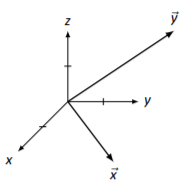
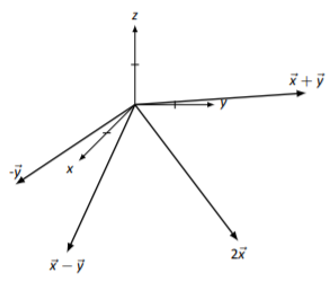
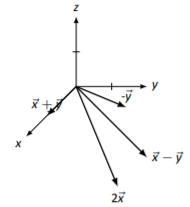
In Exercises 5.3.1.5 - 5.3.1.8, vectors →x and →y are drawn. Sketch 2→x, −→y, →x+→y, and →x−→y on the same Cartesian axes.
- Answer
-
Sketches may vary slightly.
- Answer
-
Sketches may vary slightly.
- Answer
-
Sketches may vary slightly.
- Answer
-
Sketches may vary slightly.
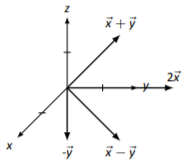
In Exercises 5.3.1.9 - 5.3.1.12, a vector →x and a scalar a are given. Using Definition 3D Vector Length, compute the lengths of →x and a→x, then compare these lengths.
→x=[1−25],a=2
- Answer
-
||→x||=√30, ||a→x||=√120=2√30
→x=[−343],a=−1
- Answer
-
||→x||=√34, ||a→x||=√34
→x=[721],a=5
- Answer
-
||→x||=√54=3√6, ||a→x||=√270=15√6
→x=[12−2],a=3
- Answer
-
||→x||=√3, ||a→x||=√27


