1.9: Divide Whole Numbers (Part 1)
- Page ID
- 4974
- Use division notation
- Model division of whole numbers
- Divide whole numbers
- Translate word phrases to math notation
- Divide whole numbers in applications
Before you get started, take this readiness quiz.
- Multiply: \(27 • 3\). If you missed this problem, review Example 1.4.6.
- Subtract: \(43 − 26\). If you missed this problem, review Example 1.3.4.
- Multiply: \(62(87)\). If you missed this problem, review Example 1.4.8.
Use Division Notation
So far we have explored addition, subtraction, and multiplication. Now let’s consider division. Suppose you have the \(12\) cookies in Figure \(\PageIndex{1}\) and want to package them in bags with \(4\) cookies in each bag. How many bags would we need?

Figure \(\PageIndex{1}\)
You might put \(4\) cookies in first bag, \(4\) in the second bag, and so on until you run out of cookies. Doing it this way, you would fill \(3\) bags.

Figure \(\PageIndex{2}\)
In other words, starting with the \(12\) cookies, you would take away, or subtract, \(4\) cookies at a time. Division is a way to represent repeated subtraction just as multiplication represents repeated addition. Instead of subtracting \(4\) repeatedly, we can write
\[12 \div 4 \nonumber \]
We read this as twelve divided by four and the result is the quotient of \(12\) and \(4\). The quotient is \(3\) because we can subtract \(4\) from \(12\) exactly \(3\) times. We call the number being divided the dividend and the number dividing it the divisor. In this case, the dividend is \(12\) and the divisor is \(4\). In the past you may have used the notation \(4 \overline{\smash{)}12}\), but this division also can be written as \(12 ÷ 4\), \(12/4\), \(\dfrac{12}{4}\). In each case the \(12\) is the dividend and the \(4\) is the divisor.
To represent and describe division, we can use symbols and words.
| Operation | Notation | Expression | Read as | Result |
|---|---|---|---|---|
| Division | ÷ | 12 ÷ 4 | Twelve divided by four | the quotient of 12 and 4 |
| \(\dfrac{a}{b}\) | \(\dfrac{12}{4}\) | |||
| \(b \overline{)a}\) | \(4 \overline{\smash{)}12}\) | |||
| a/b | 12/4 |
Division is performed on two numbers at a time. When translating from math notation to English words, or English words to math notation, look for the words of and and to identify the numbers.
Translate from math notation to words.
- \(64 ÷ 8\)
- \(\dfrac{42}{7}\)
- \(4 \overline{\smash{)}28}\)
Solution
- We read this as sixty-four divided by eight and the result is the quotient of sixty-four and eight.
- We read this as forty-two divided by seven and the result is the quotient of forty-two and seven.
- We read this as twenty-eight divided by four and the result is the quotient of twenty-eight and four.
Translate from math notation to words:
- \(84 ÷ 7\)
- \(\dfrac{18}{6}\)
- \(8 \overline{\smash{)}24}\)
- Answer a
-
eighty-four divided by seven; the quotient of eighty-four and seven
- Answer b
-
eighteen divided by six; the quotient of eighteen and six.
- Answer c
-
twenty-four divided by eight; the quotient of twenty-four and eight
Translate from math notation to words:
- \(72÷ 9\)
- \(\dfrac{21}{3}\)
- \(6 \overline{\smash{)}54}\)
- Answer a
-
seventy-two divided by nine; the quotient of seventy-two and nine
- Answer b
-
twenty-one divided by three; the quotient of twenty-one and three
- Answer c
-
fifty-four divided by six; the quotient of fifty-four and six
Model Division of Whole Numbers
As we did with multiplication, we will model division using counters. The operation of division helps us organize items into equal groups as we start with the number of items in the dividend and subtract the number in the divisor repeatedly.
Model the division: \(24 ÷ 8\).
Solution
To find the quotient \(24 ÷ 8\), we want to know how many groups of \(8\) are in \(24\).
Model the dividend. Start with \(24\) counters.

The divisor tell us the number of counters we want in each group. Form groups of \(8\) counters.
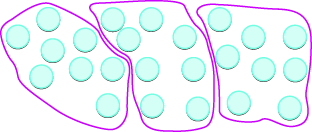
Count the number of groups. There are \(3\) groups.
\[24 \div 8 = 3 \nonumber\]
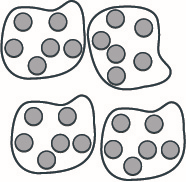
Model: \(24 ÷ 6\).
- Answer
-
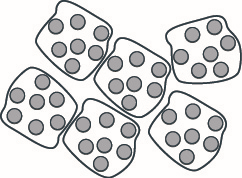
Model: \(42 ÷ 7\).
- Answer
-
Divide Whole Numbers
We said that addition and subtraction are inverse operations because one undoes the other. Similarly, division is the inverse operation of multiplication. We know \(12 ÷ 4 = 3\) because \(3 • 4 = 12\). Knowing all the multiplication number facts is very important when doing division.
We check our answer to division by multiplying the quotient by the divisor to determine if it equals the dividend. In Example \(\PageIndex{2}\), we know \(24 ÷ 8 = 3\) is correct because \(3 • 8 = 24\).
Divide. Then check by multiplying.
- \(42 ÷ 6\)
- \(\dfrac{72}{9}\)
- \(7 \overline{\smash{)}63}\)
Solution
| Divide 42 by 6. | 42 ÷ 6 = 7 |
| Check by multiplying. | 7 • 6 = 42 ✓ |
| Divide 72 by 9. | \(\dfrac{72}{9}\) |
| Check by multiplying. | 8 • 9 = 72 ✓ |
| Divide 63 by 7. | \(7 \overline{\smash{)}63}\) |
| Check by multiplying. | 9 • 7 = 63✓ |
Divide. Then check by multiplying:
- \(54 ÷ 6\)
- \(\dfrac{27}{9}\)
- Answer a
-
\(9\)
- Answer b
-
\(3\)
Divide. Then check by multiplying:
- \(\dfrac{36}{9}\)
- \(8 \overline{\smash{)}40}\)
- Answer a
-
\(4\)
- Answer b
-
\(5\)
What is the quotient when you divide a number by itself?
\[\dfrac{15}{15} = 1 \quad \text{because} \quad 1 \cdot 15 = 15 \nonumber \]
Dividing any number (except \(0\)) by itself produces a quotient of \(1\). Also, any number divided by \(1\) produces a quotient of the number. These two ideas are stated in the Division Properties of One.
| Any number (except 0) divided by itself is one. | a ÷ a = 1 |
| Any number divided by one is the same number. | a ÷ 1 = a |
Divide. Then check by multiplying:
- \(11 ÷ 11\)
- \(\dfrac{19}{1}\)
- \(1 \overline{\smash{)}7}\)
Solution
| A number divided by itself is 1. | 11 ÷ 11 = 1 |
| Check by multiplying. | 1 • 11 = 11 ✓ |
| A number divided by 1 equals itself. | \(\dfrac{19}{1} = 19\) |
| Check by multiplying. | 19 • 1 = 19 ✓ |
| A number divided by 1 equals itself. | \(1 \overline{\smash{)}7} = 7\) |
| Check by multiplying. | 7 • 1 = 7✓ |
Divide. Then check by multiplying:
- \(14 ÷ 14\)
- \(\dfrac{27}{1}\)
- Answer a
-
\(1\)
- Answer b
-
\(27\)
Divide. Then check by multiplying:
- \(\dfrac{16}{1}\)
- \(1 \overline{\smash{)}4}\)
- Answer a
-
\(16\)
- Answer b
-
\(4\)
Suppose we have \($0\), and want to divide it among \(3\) people. How much would each person get? Each person would get \($0\). Zero divided by any number is \(0\).
Now suppose that we want to divide \($10\) by \(0\). That means we would want to find a number that we multiply by \(0\) to get \(10\). This cannot happen because \(0\) times any number is \(0\). Division by zero is said to be undefined.
These two ideas make up the Division Properties of Zero.
| Zero divided by any number is 0. | 0 ÷ a = 0 |
| Dividing a number by zero is undefined. | a ÷ 0 = undefined |
Another way to explain why division by zero is undefined is to remember that division is really repeated subtraction. How many times can we take away \(0\) from \(10\)? Because subtracting \(0\) will never change the total, we will never get an answer. So we cannot divide a number by \(0\).
Divide. Check by multiplying:
- \(0 ÷ 3\)
- \(10 / 0\)
Solution
| Zero divided by any number is zero. | 0 ÷ 3 = 0 |
| Check by multiplying. | 0 • 3 = 0 ✓ |
| Dividing a number by zero is undefined. | 10/0 = undefined |
Divide. Then check by multiplying:
- \(0 ÷ 2\)
- \(17 / 0\)
- Answer a
-
\(0\)
- Answer b
-
undefined
Divide. Then check by multiplying:
- \(0 ÷ 6\)
- \(13 / 0\)
- Answer a
-
\(0\)
- Answer b
-
undefined
When the divisor or the dividend has more than one digit, it is usually easier to use the \(4 \overline{\smash{)}12}\) notation. This process is called long division. Let’s work through the process by dividing \(78\) by \(3\).
| Divide the first digit of the dividend, 7, by the divisor, 3. | |
| The divisor 3 can go into 7 two times since 2 × 3 = 6. Write the 2 above the 7 in the quotient. | 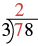 |
| Multiply the 2 in the quotient by 3 and write the product, 6, under the 7. |  |
| Subtract that product from the first digit in the dividend. Subtract 7 − 6. Write the difference, 1, under the first digit in the dividend. |  |
| Bring down the next digit of the dividend. Bring down the 8. | 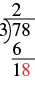 |
| Divide 18 by the divisor, 3. The divisor 3 goes into 18 six times. | 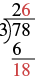 |
| Write 6 in the quotient above the 8. | |
| Multiply the 6 in the quotient by the divisor and write the product, 18, under the dividend. Subtract 18 from 18. |  |
We would repeat the process until there are no more digits in the dividend to bring down. In this problem, there are no more digits to bring down, so the division is finished. So \(78 ÷ 3 = 26\).
Check by multiplying the quotient times the divisor to get the dividend. Multiply \(26 × 3\) to make sure that product equals the dividend, \(78\).
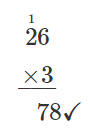
It does, so our answer is correct.
Step 1. Divide the first digit of the dividend by the divisor. If the divisor is larger than the first digit of the dividend, divide the first two digits of the dividend by the divisor, and so on.
Step 2. Write the quotient above the dividend.
Step 3. Multiply the quotient by the divisor and write the product under the dividend.
Step 4. Subtract that product from the dividend.
Step 5. Bring down the next digit of the dividend.
Step 6. Repeat from Step 1 until there are no more digits in the dividend to bring down.
Step 7. Check by multiplying the quotient times the divisor.
Divide \(2,596 ÷ 4\). Check by multiplying.
Solution
| Let's rewrite the problem to set it up for long division. | 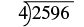 |
| Divide the first digit of the dividend, 2, by the divisor, 4. |  |
| Since 4 does not go into 2, we use the first two digits of the dividend and divide 25 by 4. The divisor 4 goes into 25 six times. | |
| We write the 6 in the quotient above the 5. |  |
| Multiply the 6 in the quotient by the divisor 4 and write the product, 24, under the first two digits in the dividend. |  |
| Subtract that product from the first two digits in the dividend. Subtract 25 − 24 . Write the difference, 1, under the second digit in the dividend. | 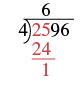 |
| Now bring down the 9 and repeat these steps. There are 4 fours in 19. Write the 4 over the 9. Multiply the 4 by 4 and subtract this product from 19. | 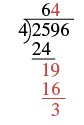 |
| Bring down the 6 and repeat these steps. There are 9 fours in 36. Write the 9 over the 6. Multiply the 9 by 4 and subtract this product from 36. |  |
| Check by multiplying. | 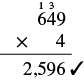 |
It equals the dividend, so our answer is correct. So \(2,596 ÷ 4 = 649\).
Divide. Then check by multiplying: \(2,636 ÷ 4\).
- Answer
-
\(659\)
Divide. Then check by multiplying: \(2,716 ÷ 4\).
- Answer
-
\(679\)
Divide \(4,506 ÷ 6\). Check by multiplying.
Solution
| Let's rewrite the problem to set it up for long division. | 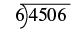 |
| First we try to divide 6 into 4. |  |
| Since that won't work, we try 6 into 45. There are 7 sixes in 45. We write the 7 over the 5 | 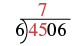 |
| Multiply the 7 by 6 and subtract this product from 45. | 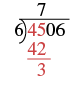 |
| Now bring down the 0 and repeat these steps. There are 5 sixes in 30. Write the 5 over the 0. Multiply the 5 by 6 and subtract this product from 30. |  |
| Now bring down the 6 and repeat these steps. There is 1 six in 6. Write the 1 over the 6. Multiply 1 by 6 and subtract this product from 6. |  |
| Check by multiplying. |  |
It equals the dividend, so our answer is correct.
Divide. Then check by multiplying: \(4,305 ÷ 5\).
- Answer
-
\(861\)
Divide. Then check by multiplying: \(3,906 ÷ 6\).
- Answer
-
\(651\)
Divide \(7,263 ÷ 9\). Check by multiplying.
Solution
| Let's rewrite the problem to set it up for long division. | 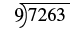 |
| First we try to divide 9 into 7. | 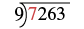 |
| Since that won't work, we try 9 into 72. There are 8 nines in 72. We write the 8 over the 2. |  |
| Multiply the 8 by 9 and subtract this product from 72. |  |
| Now bring down the 6 and repeat these steps. There are 0 nines in 6. Write the 0 over the 6. Multiply the 0 by 9 and subtract this product from 6. |  |
| Now bring down the 3 and repeat these steps. There are 7 nines in 63. Write the 7 over the 3. Multiply the 7 by 9 and subtract this product from 63. |  |
| Check by multiplying. | 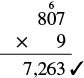 |
It equals the dividend, so our answer is correct.
Divide. Then check by multiplying: \(4,928 ÷ 7\).
- Answer
-
\(704\)
Divide. Then check by multiplying: \(5,663 ÷ 7\).
- Answer
-
\(809\)
So far all the division problems have worked out evenly. For example, if we had \(24\) cookies and wanted to make bags of \(8\) cookies, we would have \(3\) bags. But what if there were \(28\) cookies and we wanted to make bags of \(8\)? Start with the \(28\) cookies as shown in Figure \(\PageIndex{3}\).

Figure \(\PageIndex{3}\)
Try to put the cookies in groups of eight as in Figure \(\PageIndex{4}\).
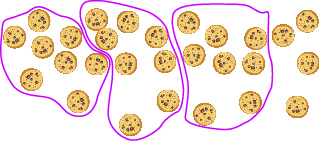
Figure \(\PageIndex{4}\)
There are \(3\) groups of eight cookies, and \(4\) cookies left over. We call the \(4\) cookies that are left over the remainder and show it by writing \(R4\) next to the \(3\). (The \(R\) stands for remainder.)
To check this division we multiply \(3\) times \(8\) to get \(24\), and then add the remainder of \(4\).

Divide \(1,439 ÷ 4\). Check by multiplying.
Solution
| Let's rewrite the problem to set it up for long division. |  |
| First we try to divide 4 into 1. Since that won't work, we try 4 into 14. There are 3 fours in 14. We write the 3 over the 4. |  |
| Multiply the 3 by 4 and subtract this product from 14. | 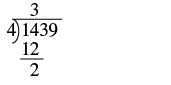 |
| Now bring down the 3 and repeat these steps. There are 5 fours in 23. Write the 5 over the 3. Multiply the 5 by 4 and subtract this product from 23. | 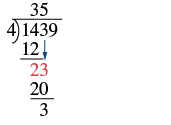 |
| Now bring down the 9 and repeat these steps. There are 9 fours in 39. Write the 9 over the 9. Multiply the 9 by 4 and subtract this product from 39. There are no more numbers to bring down, so we are done. The remainder is 3. | 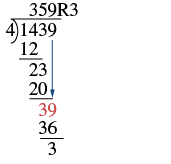 |
| Check by multiplying. |  |
So \(1,439 ÷ 4\) is \(359\) with a remainder of \(3\). Our answer is correct.
Divide. Then check by multiplying: \(3,812 ÷ 8\).
- Answer
-
\(476\) with a remainder of \(4\)
Divide. Then check by multiplying: \(4,319 ÷ 8\).
- Answer
-
\(539\) with a remainder of \(7\)
Divide and then check by multiplying: \(1,461 ÷ 13\).
Solution
| Let's rewrite the problem to set it up for long division. | 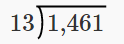 |
| First we try to divide 13 into 1. Since that won't work, we try 13 into 14. There is 1 thirteen in 14. We write the 1 over the 4. |  |
| Multiply the 1 by 13 and subtract this product from 14. | 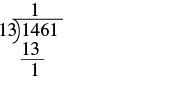 |
| Now bring down the 6 and repeat these steps. There is 1 thirteen in 16. Write the 1 over the 6. Multiply the 1 by 13 and subtract this product from 16. |  |
| Now bring down the 1 and repeat these steps. There are 2 thirteens in 31. Write the 2 over the 1. Multiply the 2 by 13 and subtract this product from 31. There are no more numbers to bring down, so we are done. The remainder is 5. 1,462 ÷ 13 is 112 with a remainder of 5. | 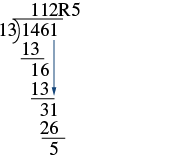 |
| Check by multiplying. |  |
Our answer is correct.
Divide. Then check by multiplying: \(1,493 ÷ 13\).
- Answer
-
\(114\) R \(11\)
Divide. Then check by multiplying: \(1,461 ÷ 12\).
- Answer
-
\(121\) R \(9\)
Divide and check by multiplying: \(74,521 ÷ 241\).
Solution
| Let's rewrite the problem to set it up for long division. | 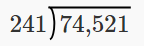 |
| First we try to divide 241 into 7. Since that won’t work, we try 241 into 74. That still won’t work, so we try 241 into 745. Since 2 divides into 7 three times, we try 3. Since 3 × 241 = 723, we write the 3 over the 5 in 745. Note that 4 would be too large because 4 × 241 = 964, which is greater than 745. | |
| Multiply the 3 by 241 and subtract this product from 745. | 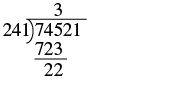 |
| Now bring down the 2 and repeat these steps. 241 does not divide into 222. We write a 0 over the 2 as a placeholder and then continue. | 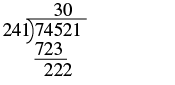 |
| Now bring down the 1 and repeat these steps. Try 9. Since 9 × 241 = 2,169, we write the 9 over the 1. Multiply the 9 by 241 and subtract this product from 2,221. |  |
| There are no more numbers to bring down, so we are finished. The remainder is 52. So 74,521 ÷ 241 is 309 with a remainder of 52. | |
| Check by multiplying. |  |
Sometimes it might not be obvious how many times the divisor goes into digits of the dividend. We will have to guess and check numbers to find the greatest number that goes into the digits without exceeding them.
Divide. Then check by multiplying: \(78,641 ÷ 256\).
- Answer
-
\(307\) R \(49\)
Divide. Then check by multiplying: \(76,461 ÷ 248\).
- Answer
-
\(308\) R \(77\)
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.


